tensorflow1.x学习笔记（2）：激活函数、损失函数、优化算法、学习率、过拟合问题

1深度学习与深层神经网络

1.1 线性模型的局限性

在线性可分的问题中，线性模型的表现效果非常好，但是对于线性不可分问题，线性模型的表现并不是很好。因此对于线性不可分问题，线性模型存在局限性。

1.2 激活函数实现去线性化

如果将每一个神经元的输出都通过一个非线性函数，那么整个网络的模型就不再是线性的，这个非线性函数就是激活函数。
常用的激活函数有sigmoid函数、relu函数和tanh函数，函数的表达式和图像如下所示：

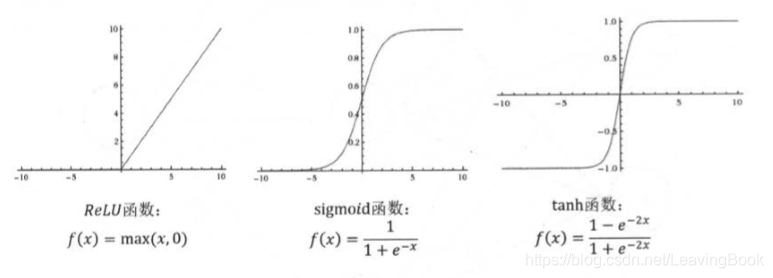
在tensorlfow1.x中，调用他们的方式为tf.nn.relu、tf.sigmoid、tf.tanh
实现下图的前向传播算法：

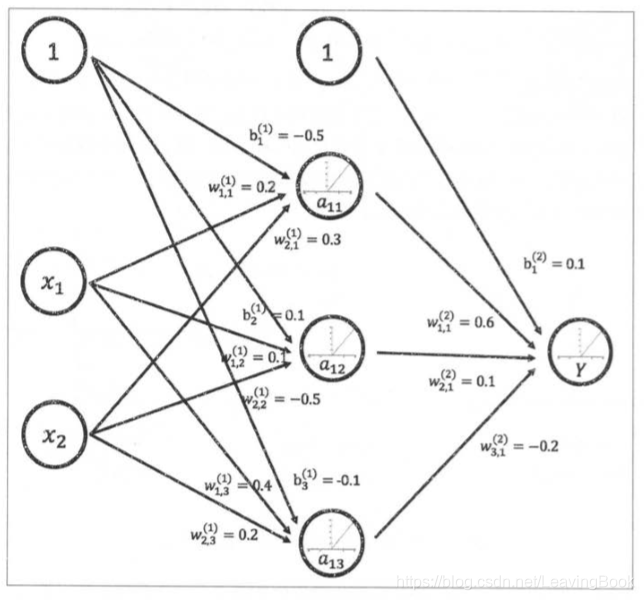
a = tf.nn.relu(tf.matmul(x, w1) + biases1)
y = tf.nn.relu(tf.matmul(a, w2) + biases2)

2 损失函数的定义

2.1 经典的损失函数

判断网络输出向量与期望的向量的接近程度，通过交叉熵 cross entropy可以进行判断。交叉熵刻画了两个概率分布之间的距离，是分类问题中比较常用的一种损失函数。它原本是信息论中的概念，给定两个概率分布p和q，通过q来表示p的交叉熵为：
$$H(p,q)=-\sum _{x}p(x)logq(x)$$
注意交叉熵刻画的是两种概率分布之间的距离，然而神经网络的输出却不一定是概率分布。一般通过softmax回归将神经网络前向传播的结果变成概率分布。假设原始神经网络输出为y1,y2,…,yn,那么经过softmax回归之后的输出为：
$$softmax(y{)}_i=y_i^{{}^{\prime }}=\frac{e^{yi}}{{\sum }_{j=1}^n{e}^{yi}}$$
通过上面的公式就把神经网络的输出也变成了一个概率分布，从而可 以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。
举个例子，如果某个样例的正确答案为(1,0,0)，某个模型经过softmax回归之后的预测答案是(0.5,0.4,0.1)，那么预测答案与正确答案之间的交叉熵为
$$H((1,0,0),(0.5,0.4,0.1)=-(1\times log0.8+0\times log0.4+0\times 0.1))\approx 0.3$$

# tensorflow实现交叉熵
# y表示预测结果  y_代表正确结果
cross_entropy = -tf.reduce_mean(
    y_*tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
    #注意*是两元素直接相乘，并不是矩阵乘法

# tf.clip_by_value 的应用
v = tf.constant([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])
with tf.Session() as sess: 
    print (tf.clip_by_value(v, 2.5, 4.5).eval())
    #小于2.5的数字都成了2.5，大于4.5的数字都换成了4.5
  '''
  输出：
  [[2.5 2.5 3. ]
 [4.  4.5 4.5]]
  '''

v = tf.constant([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])
with tf.Session() as sess:
    print(tf.reduce_mean(v).eval())
# 21 / 6 = 3.5 求均值

可以通过下面的代码直接实现softmax回归后的交叉熵损失函数

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(
	labels = _y, logits = y)

对于回归问题通常用到的损失函数为均方误差（MSE），定义如下所示：
$$MSE(y,y^{{}^{\prime }})=\frac{{\sum }_{i=1}^n(y_i-y_i^{{}^{\prime }}{)}^2}{n}$$
通过tensorflow实现如下:

mse = tf.reduce_mean(tf.sqare(y_- y))

2.2 自定义损失函数

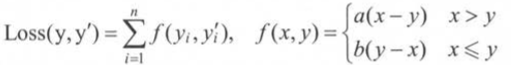
loss = tf.reduce_sum(tf.where(tf.greater(v1,v2),
	(v1-v2) * a, (v2 - v1) * b))

3 神经网络优化算法

对于梯度下降算法，假设用 θ 表示神经网络中的参数， J（θ）表示在给定的参数取值下，训练数据集上损失 函数的大小，那么整个优化过程可以抽象为寻找一个参数θ ，使得 J（θ）最小。

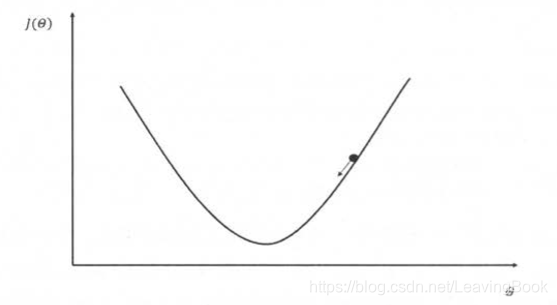
梯度下降的公式为：
$${\theta }_{n+1}={\theta }_n-\eta \frac{\partial }{\partial {\theta }_n}J({\theta }_n)$$
神经网络的优化过程可以分为两个阶段，第一个阶段通过前向传播算法计算得到预测值，并将预测值和真实值做对比得出两者之间的差距。 然后在第二个阶段通过反向传播算法计算损失函数对每一个参数的梯度，再根据梯度和学习率使用梯度下降算法更新每一个参数。
需要注意的是梯度下降算法并不能保证得到全局的最优解，只有在凸函数的情况下才能得到全局最优解。
另一个问题就是梯度下降算法所需要的时间太长。为了解决这个问题可以使用随机梯度下降算法，但是最后得到的效果并不太好。
神经网络的训练流程大致如下所示：

batch_size = n

#每次读取一小部分数据作为当前训练数据来执行反向传播算法
x = tf.placeholder(tf.float32, shape=(batch_size,2), name = 'x-input')
y_ = tf.placeholder(tf.float32, shape=(batch_size, 1), name = "y-input")

#定义神经网络结构和优化算法
loss = ...
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

#训练神经网络
with tf.Session() as sess:
    #参数初始化
    ...
    # 迭代更新参数
    for i in range(STEPS):
        # 准备batch_size个训练数据。一般将所有训练数据随机打乱之后再选取可以得到的
        # 更好的优化效果
        current_X, ...
        sess.run()

4 神经网络的进一步优化

4.1 学习率的设置

在训练神经网络的过程中，需要设置学习率（learning rate）来控制参数的更新的速度。学习率决定了参数每次更新的幅度。 如果幅度过大， 那么可能导致参数在极优值的两侧来回移动。如果幅度过小又会导致迭代多次之后也没有下降到最低点。因此，学习率的设置不能过大也不能太小。
TensorFlow 提供了一种更加灵活的学习率设置方法一一指数衰减法。 过这个函数，可以先使用较大的学 习率来快速得到一个比较优的解，然后随着迭代的继续逐步减小学习率，使得模型在训练后 期更加稳定。还可以通过tf.train.exponential_decay。

decayed_learning_rate =  learning_rate * decay_rate ^ (global_step / decay_steps)
# decayed_learning_ rate  每一轮优化使用的学习率
# learning_rate  事先设定好的学习率 
# decay_rate 衰减系数
# decay_steps 衰减速度

global_step = tf.Variable(0)

# 通过exponetial_decay 函数生成学习率
learning_rate = tf.train.exponetial_decay(
    0.1, global_step, 100, 0.96, staircase= True)


# 使用指数衰减的学习率。在 minimize 函数中传入 global_step 将自动更新
# global_step 参数，从而使得学习率也得到相应更新。
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize()

4.2 过拟合问题

有些时候经过训练后的模型会产生过拟合的问题，从而无法分表样本中的噪声点。为了避免过拟合问题，一个非常常用的方法就是进行正则化，分别有L1正则化和L2正则化。此时优化的损失函数变为
$$J(\theta )+\lambda R(w)$$
L1正则化：
$$R(w)=\parallel w{\parallel }_1=\sum _i|w_i|$$
L2正则化：
$$R(w)=\parallel w{\parallel }_2^2=\sum _i|w_i^2|$$
也可将L1正则化和L2正则化联合使用
$$R(w)=\sum _i\alpha |w_i|+(1-\alpha )w_i^2$$
无论是哪一种正则化方式，基本的思想都是希望通过限制权重的大小，使得模型不能 任意拟合训练数据中的随机噪音。

weights = tf.constant([[1.0, -2.0],[-3.0, 4.0]])
with tf.Session() as sess:
    # 输出为所有绝对值相加×0.5
    print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(weights))) # 5.0
    # 输出为所有的权值每个的平方加起来除以二乘以0.5
    print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(weights))) # 7.5

4.3 滑动平均模型

待续

参考资料：《TensorFlow实战Google深度学习框架（第2版）》