JZOJ7月15日提高组T4 排列统计

最新推荐文章于 2020-07-29 16:53:32 发布

原创最新推荐文章于 2020-07-29 16:53:32 发布 · 143 阅读

2 ·

CC 4.0 BY-SA版权

本文解析了一个排列统计问题，探讨了如何计算满足特定条件的序列数量。通过分析序列特性，利用矩阵辅助理解，详细阐述了解题思路及算法实现，适用于算法竞赛和高级编程爱好者。

JZOJ7月15日提高组T4 排列统计

题目
题解
- 分析
- Code

题目

Description

对于给定的一个长度为n的序列{B[n]}，问有多少个序列{A[n]}对于所有的i满足：A[1]～A[i]这i个数字中有恰好B[i]个数字小等于i。其中{A[n]}为1～n的一个排列，即1～n这n个数字在序列A[I]中恰好出现一次。
数据保证了至少有一个排列满足B序列。

Input

输入的第1行为一个正整数N，表示了序列的长度。
第2行包含N个非负整数，描述了序列{B[i]}。

Output

输出仅包括一个非负整数，即满足的{A[i]}序列个数。

Sample Input

3
0 1 3

Sample Output

Data Constraint

对于20%的数据，有N≤8；
对于30%的数据，有N≤11且答案不大于20000；
对于50%的数据，有N≤100；
对于100%的数据，有N≤2000。

Hint

对于A序列为1～3的全排列分别对应的B序列如下（冒号左边为A序列，冒号右边为对应B的序列）
1 2 3：1 2 3
1 3 2：1 1 3
2 1 3：0 2 3
2 3 1：0 1 3
3 1 2：0 1 3
3 2 1：0 1 3
所以有3个满足的A序列。

题解

分析

借助矩阵来分析
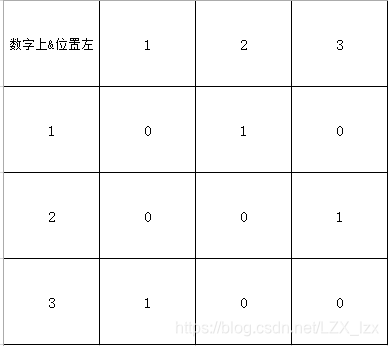
在这里插入图片描述
上面这张图片代表的是序列2,3,1
那么 $b [i]$ 就代表这 $(1, 1)$ 到 $(i, i)$ 内1的数量
~~显而易见~~发现 $b [i]$ 和 $b [i + 1]$ 之间的差只有0、1、2三种情况
设 $f [i]$ 表示到第 $i$ 位置时，只考虑选前 $i$ 个数的方案数
分类讨论

当 $b [i] - b [i - 1] = 0$ 时， $f [i] = f [i - 1]$
当 $b [i] - b [i - 1] = 1$ 时， $f [i] = f [i - 1] * [(i - a [i - 1]) + (i - a [i - 1] - 1]$
当 $b [i] - b [i - 1] = 2$ 时， $f[i]=f[i-1]*(i-a[i-1]-1)^2$

要使用高精度~~（duliu）~~

Code

#include<cstdio>
#include<cstring>
using namespace std;
int n,i,a[2005];
long long c[10005],ans[10005];
void gjd(long long s)
{
	int i,j,num;
	long long x;
	for (i=1;i<=ans[0];i++)
		ans[i]*=s;
	i=1;
	while (i<=ans[0])
	{
		ans[i+1]+=ans[i]/10;
		ans[i]%=10;
		i++;
		if (i>ans[0]&&ans[i]!=0) 
			ans[0]++;
	}
}
int main()
{
	freopen("input.in","r",stdin);
	scanf("%d",&n);
	for (i=1;i<=n;i++)
		scanf("%d",&a[i]);
	ans[0]=1;
	ans[1]=1;
	for (i=2;i<=n;i++)
	{
		if (a[i]-a[i-1]==1) 
			gjd(i-a[i-1]+i-1-a[i-1]);
		if (a[i]-a[i-1]==2) 
			gjd((i-a[i-1]-1)*(i-a[i-1]-1));
	}
	for (i=ans[0];i>=1;i--)
		printf("%d",ans[i]);
	printf("\n");
	return 0;
}