本文介绍了MATLAB中的符号计算功能，包括符号常量与变量的定义、符号表达式的操作、微积分运算、方程求解等内容，并展示了如何利用MATLAB进行矩阵运算、傅里叶变换及常见统计分析。
目录
九、如何执行傅里叶变换，以及如何将信号通过傅里叶变换转换到频域？
九、如何使用矩阵分解技术，例如奇异值分解和特征值分解，来解决各种数学问题？
一、符号计算简介
MATLAB符号计算功能是MATLAB中的一种强大的工具，它使用户能够进行符号计算和代数运算，而不仅仅是数值计算。
MATLAB符号计算功能可以处理符号表达式、方程、微积分和代数式等数学对象。用户可以使用符号计算功能求解方程组、求导、积分、解微分方程等复杂的计算问题。
MATLAB中的符号计算功能包括符号计算工具箱和符号计算命令。其中符号计算工具箱提供了大量的函数和工具，可以用来处理符号式、方程组、求导、积分、代数式化简、三角式化简等。而符号计算命令则是用户在MATLAB命令窗口中输入的命令，用于完成符号计算任务。
总而言之，MATLAB符号计算功能是MATLAB中非常强大的工具，它为用户提供了一种更广泛的数学计算和探索方式，让用户能够更便捷地进行符号计算和代数运算。
二、常量
1.符号常量和符号变量
创建的这个符号对象可以用class（）函数来检测其数据类型。用sym（）函数创建符号变量的一般格式为：
sym(常量) %创建符号常量
sym(常量,参数） %把常量按“参数”指定的格式转换为符号常量
例：定义符号常量1/3，并判断变量类型
>> a=1/3;
>> b=sym(1/3); %定义1/3为符号常量
>> c=class(a) %查询a的常量类型
c =
double
>> d=class(b) %查询b的常量类型
d =
sym2.定义符号变量
（1）用sym()函数定义符号变量
格式：
sym(‘varname’,parameter)
sym(expression)其中，varname表示创建符号变量的名称；expression表示符号表达式。parameter可以用来设置限定符号变量的数学特性，可以选择为poasitive、real和unreal,分别表示正数、实数和负实数。
例.做符号计算：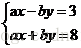
式中a,b,x,y均为符号常量。在符号运算前，应先将变量a,b,x,y定义为符号常量
>> a=sym('a')
a =
a
>> a=sym('a');
>> b=sym('b');
>> x=sym('x');
>> y=sym('y');
>> [x,y]=solve(a*x-b*y-3,a*x+b*y-8,x,y)
x =
11/(2*a)
y =
5/(2*b)
（2）使用syms()函数定义符号常量
格式：
syms(‘arg1’,’arg2’,...,参数） %把字符常量定义为符号常量
syms arg1 arg2 ...参数 %把字符变量定义为符号变量的简洁形式
（3）默认符号变量
| 编号 | 符号表达式 | 默认符号变量 | 编号 | 符号表达式 | 默认符号变量 |
| 1 | a*x^3+b*x+c | x | 4 | 18*a+b | b |
| 2 | 1/(3+cos(t)) | t | 5 | 2*i | i |
| 3 | 10*x/y | x |
三、表达式
1.符号表达式
符号表达式例子
| 符号表达式 | MATLAB表达式 |
|
| ‘1/(3*x^n)’ |
|
| y=’1/sqrt(6*x)’ |
|
| ‘cos(x^3)-sin(3*x)’ |
|
| M=sym(‘[1,2;3,4]’)a |
例：使用sym （）函数创建符号表达式f=ax+b
>> syms a x b
>> f=a*x+b
f =
b + a*x2.符号表达式运算
（1）提取分子和分母
语法格式：[N,D]=numden(expression)
N为通分后的分子，D为通分后的分母
例：求符号表达式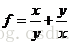
的分子和分母
>> syms x y;
>> f=x/y+y/x;
>> [N,D]=numden(f)
N =
x^2 + y^2
D =
x*y（2）标准代数运算
格式：
sym(expression1)+sym(expression2) %符号表达式加运算
sym(expression1)-sym(expression2) %符号表达式减运算
sym(expression1)*sym(expression2) %符号表达式乘运算
sym(expression1)/sym(expression2) %符号表达式除运算
例.给定符号表达式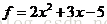
和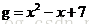
，请给出两个符号表达式进行加，减，乘，除运算的结果
>> f='2*x^2+3*x-5'
f =
2*x^2+3*x-5
>> g='x^2-x+7'
g =
x^2-x+7
>> sym(f)+sym(g)
ans =
3*x^2 + 2*x + 2
>> sym(f)-sym(g)
ans =
x^2 + 4*x - 12
>> sym(f)*sym(g)
ans =
(x^2 - x + 7)*(2*x^2 + 3*x - 5)
>> sym(f)/sym(g)
ans =
(2*x^2 + 3*x - 5)/(x^2 - x + 7)
（3）高级运算
a.使用compose()函数实现函数复合
格式：Expression3=compose(expression1,expression2)
例.给定表达式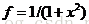
和g=sin(x),请计算f(g(x))和g(f(x))的结果
>> syms x;
>> syms u v
>> f=1/(1+x^2)
f =
1/(x^2 + 1)
>> g=sin(x)
g =
sin(x)
>> h=1/(1+u^2)
h =
1/(u^2 + 1)
>> k=sin(v)
k =
sin(v)
>> compose(f,g)
ans =
1/(sin(x)^2 + 1)
>> compose(g,f)
ans =
sin(1/(x^2 + 1))
>> compose(h,k,'u','v')
ans =
1/(sin(v)^2 + 1)b.使用finverse()函数求反函数
格式：finverse(expression1,varname)
varname为自变量，expression为符号表达式。finverse()函数对指定自变量varname的函数expression1(varname)求反函数，当varname省略，则对默认的自由符号变量求反函数
例：求1/x,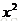
和ax+b的逆函数
>> syms a b
>> finverse(1/x)
ans =
1/x
>> finverse(x^2)
ans =
x^(1/2)
>> finverse(a*x+b)
ans =
-(b - x)/a（4）使用symsun()函数对级数求和
语法格式：
r=symsum(s) %对符号表达式s中的默认符号变量k从0到k-1求和
r=symsum(s，v) %对符号表达式s中的指定符号变量v从0到v-1求和
r=symsum(s,a,b) %对符号表达式s中的指定符号变量v从a到b求和
r=symsum(s,v,a,b) %对符号表达式s中的默认符号变量k从a到b求和
例：求级数1/12+1/22+1/32+1/42+...的和及其前10项的部分和
>> syms k
>> symsum(1/k^2,1,inf)
ans =
pi^2/6
>> double(ans)
ans =
1.6449四、符号微分和积分
1.符号极限limit
| 命令格式 | 说明 |
| limit(expression,x,a) | 计算符号表达式x→a时，F的极限值 |
| limit(expression,a) | 计算符号函数F的极限值，因未指定F的自变量，用该格式时，变量为findsym确定默认自变量，即默认自变量→a |
| limit(expression) | 计算符号函数F的极限值，变量findsym确定的默认变量；在未指定目标值时，默认变量趋近于0 |
| limit(expression,x,a,’left’) | 计算当x→a时函数F的左极限 |
| limit(expression,x,a,’right’) | 计算当x→a时函数F的右极限 |
例.求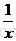
的左右极限
>> syms x t;
>> limit(1/x,x,0,'right')
ans =
Inf
>> limit(1/x,x,0,'left')
ans =
-Inf2.符号微分
| 命令格式 | 说明 |
| diff(f,v,n) | 表示以v为变量，对符号表达式f求n阶微分 |
| diff(f,v)或diff(f,sym(‘v’)) | 表示以v为自变量，对符号表达式f求一阶微分 |
| diff(f,n) | 表示根据findsym指示的默认变量对符号表达式f求n阶微分 |
| diff(f) | %表示没有指定微分变量和微分阶数，则按findsym指示的默认变量对符号表达式f求一阶微分 |
例.使用符号运算计算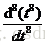
>> f=sym('t^8')
f =
t^8
>> diff(f,8)
ans =
403203.符号积分
| 命令格式 | 说明 |
| int(f,’v’,a,b) | 表示以v为变量，对符号表达式f求a到b的定积分 |
| int(f,’v’)或int(f,’v’) | 表示v为自变量，对符号表达式f求不定积分 |
| int(f,a,b) | 根据findsym指示的默认变量对符号表达式f求a到b的定积分 |
| int(f) | 按findsym指示的默认变量对符号表达式f求不定积分。如果f是常数，积分将针对x |
例.分别计算表达式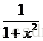
和
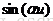对α的积分
>> syms x x1 alpha u t;
>> int(1/(1+x^2))
ans =
atan(x)
>> int(sin(alpha*u),alpha)
ans =
-cos(alpha*u)/u五、方程
1.方程求解
（1）求解代数方程组
格式：
g=solve(equation)
g=solve(equation,var)
g=solve(equation1,equation2,..,equationn)
g=solve(equation1,equation2,..,equationn,var1,var2,..varn)例.求解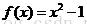
>> syms x
>> f=x^2-1;
>> solve(f)
ans =
1
-1（2）单个微分方程
格式：
r=dsplve(‘eq1,eq2,...’,’cond1,cond2,...’,’var’)
r=dsplve(‘eq1’,’eq2’,...’,’cond1’,’cond2’,...’,’var’)例.求解微分方程f’=f+cos(t)
>> dsolve('Df=f+cos(t)')
ans =
sin(t)/2 - cos(t)/2 + C5*exp(t)(3)微分方程组
例.求解微分方程组x’=y,y’=x
>> A=dsolve('Dx=y','Dy=-x')
A =
y: [1x1 sym]
x: [1x1 sym]
>> A.x
ans =
C6*cos(t) + C7*sin(t)
>> A.y
ans =
C7*cos(t) - C6*sin(t)2.线性代数和矩阵
（1）符号矩阵的创建
a.用字符串直接创建矩阵
例：
>> A=['[ a,2*b]';'[3*a, 0]']
A =
[ a,2*b]
[3*a, 0]b.用sym()函数创建矩阵
例：
>> A=sym('[ a,2*b;3*a, 0]')
A =
[ a, 2*b]
[ 3*a, 0]c.用syms()函数创建矩阵
格式：syms arg1 arg2...参数
A=[]
例：
>> syms a b
>> A=[a,2*b;3*a,0]
A =
[ a, 2*b]
[ 3*a, 0]d.将数值矩阵转化成符号矩阵
例.已知数值矩阵[2/3,sqrt(2);5.2,log(3)],试将该矩阵装换为符号矩阵
>> B=[2/3,sqrt(2);5.2,log(3)]
B =
0.6667 1.4142
5.2000 1.0986六、符号矩阵相关函数
1、矩阵变换函数
| 函数名称 | 函数功能说明 |
| flipud(A) | 将矩阵A上下翻转 |
| fliplr(A) | 将矩阵A左右翻转 |
| flidim(A,dim) | 将矩阵A沿特定dim维翻转 |
| rot90(A) | 将矩阵A逆时针旋转90度 |
| reshape(A,M,N) | 将矩阵A变维成M*N阶的 |
2、矩阵运算函数
| 函数名称 | 函数功能说明 | 函数名称 | 函数功能说明 |
| chol | 矩阵的Cholesky分解 | logm() | 矩阵的对数函数 |
| cond | 矩阵的条件数 | lu() | 矩阵的LU分解 |
| condieg | 对应于特征值的条件数 | svd() | 矩阵的奇异值分解 |
| det | 方阵的行列式值 | norm() | 向量矩阵的范数 |
| eig | 矩阵的特征值分解 | squtm() | 矩阵的平方根 |
| expm | 矩阵的指数函数 | subspace() | 子空间的夹角 |
| funm | 计算矩阵的函数值 | jacobian() | 求矩阵的jacobian矩阵 |
| inv | 求矩阵的逆矩阵 | jordan() | 求矩阵的jordanb标准型 |
| rank | 矩阵的秩 | qr() | 矩阵的QB分解 |
| orth | 矩阵的列空间 |
七、如何求解矩阵的特征值、特征向量、方阵的逆、行列式等？
1.求解矩阵的特征值和特征向量
MATLAB提供了eig函数用于求解矩阵的特征值和特征向量。该函数的使用方法如下：
[V, D] = eig(A)
其中，A为输入的矩阵，V是特征向量组成的矩阵，D是特征值构成的对角矩阵。
例如，对于一个3x3的矩阵A，可以使用以下代码求解其特征值和特征向量：
A = [2 -1 0; -1 2 -1; 0 -1 2];
[V, D] = eig(A)
输出结果为：
V =
-0.7071 -0.0000 0.7071
0.0000 -0.7071 -0.7071
0.7071 0.7071 -0.0000
D =
1.0000 0 0
0 2.0000 0
0 0 3.0000
2.求解方阵的逆
MATLAB提供了inv函数用于求解方阵的逆。该函数的使用方法如下：
B = inv(A)
其中，A为输入的方阵，B为其逆矩阵。
例如，对于一个3x3的方阵A，可以使用以下代码求解其逆矩阵：
A = [2 -1 0; -1 2 -1; 0 -1 2];
B = inv(A)
输出结果为：
B =
4.0000 3.0000 4.0000
3.0000 4.0000 3.0000
4.0000 3.0000 4.0000
需要注意的是，inv函数只接受输入的是方阵。
3.求解行列式
MATLAB提供了det函数用于求解方阵的行列式。该函数的使用方法如下：
d = det(A)
其中，A为输入的方阵，d为其行列式。
例如，对于一个3x3的方阵A，可以使用以下代码求解其行列式：
A = [2 -1 0; -1 2 -1; 0 -1 2];
d = det(A)
输出结果为：
d =
4
八、如何求解给定的差分方程？
在MATLAB中，有几种方法可以求解差分方程：
-
使用符号计算工具箱（Symbolic Math Toolbox）求解差分方程。该工具箱包含函数dsolve（）用于求解符号差分方程。
-
使用数值方法求解差分方程。该方法可以使用MATLAB的ode45（）函数等求解器来求解微分方程。差分方程也可以转化为微分方程，并使用这些求解器来求解它们。
-
使用Z变换变换差分方程，将其转换为连续时间系统，并使用MATLAB的控制系统工具箱（Control System Toolbox）中的函数来求解。
下面是一个使用符号计算工具箱来求解差分方程的例子：
假设有一个二阶差分方程y(n)-2y(n-1)+y(n-2)=x(n)，其中y(0)=0，y(1)=0，x(n)是一个给定的序列。
代码如下：
syms y(n) x(n) eqn = y(n)-2*y(n-1)+y(n-2) == x(n); cond = [y(0)==0, y(1)==0]; sol = dsolve(eqn, cond); ySol(n) = simplify(sol);
现在ySol（）函数包含了差分方程的解。可以使用matlabFunction（）函数将其转换为可执行的MATLAB函数：
y = matlabFunction(ySol(n));
要求解差分方程，请提供序列x（n）并调用MATLAB函数y（n）：
n = 0:10; x = sin(n); y = y(n); stem(n, y); xlabel('n') ylabel('y(n)') title('Solution of Difference Equation')
九、如何执行傅里叶变换，以及如何将信号通过傅里叶变换转换到频域？
MATLAB可以使用fft函数执行快速傅里叶变换（FFT），ifft函数执行逆快速傅里叶变换（IFFT），fft2函数执行二维FFT，ifft2函数执行二维IFFT。通过FFT函数执行傅里叶变换，可以将信号从时域转换到频域。具体步骤如下：
-
构造时间序列t和信号向量x（也可以从文件中读取）。
-
通过FFT函数将信号x从时域转换到频域。此时得到的是复数数组，包括实部和虚部。
-
通过abs函数对复数数组取模，可以得到振幅谱（即信号在频域中的振幅分布）。
-
通过angle函数对复数数组取相角，可以得到相位谱（即信号在频域中的相位分布）。
-
通过fftshift函数可以将FFT的结果按照频率进行移位，使得低频部分在中心，高频部分在两侧。
-
可以使用plot函数绘制振幅谱和相位谱，以便更好地观察信号在频域中的特征。
下面是一个简单的例子，展示如何将信号通过FFT转换到频域：
% 构造时间序列和信号
Fs = 1000; % 采样频率为1000Hz
t = 0:1/Fs:1-1/Fs; % 时间序列从0到1秒
x = cos(2*pi*50*t) + 0.5*sin(2*pi*120*t); % 构造信号
% 执行FFT
N = length(x); % 信号长度
X = fft(x)/N; % 执行FFT并归一化
f = (0:N-1)*(Fs/N); % 构造频率向量
% 绘制振幅谱和相位谱
subplot(2,1,1)
plot(f,abs(X)) % 绘制振幅谱
title('振幅谱')
xlabel('频率 (Hz)')
ylabel('振幅')
subplot(2,1,2)
plot(f,angle(X)) % 绘制相位谱
title('相位谱')
xlabel('频率 (Hz)')
ylabel('相位 (弧度)')
% 将FFT结果按照频率移位
Xshift = fftshift(X);
fshift = (-N/2:N/2-1)*(Fs/N);
% 绘制移位后的振幅谱和相位谱
figure
subplot(2,1,1)
plot(fshift,abs(Xshift))
title('移位后的振幅谱')
xlabel('频率 (Hz)')
ylabel('振幅')
subplot(2,1,2)
plot(fshift,angle(Xshift))
title('移位后的相位谱')
xlabel('频率 (Hz)')
ylabel('相位 (弧度)')
八、如何找到给定函数的最小值或最大值？
MATLAB中有多种方法可以找到给定函数的最小值或最大值，以下是几种常用的方法：
1.fminsearch函数 fminsearch是MATLAB中的优化函数，可以在不需要计算函数导数的情况下寻找函数的最小值。使用方法如下：
x = fminsearch(fun, x0)
其中，fun是需要寻找最小值的函数句柄，x0是初始点的向量。该函数将返回使函数最小的x向量。
2.fminbnd函数 fminbnd也是MATLAB中的优化函数，专门用于寻找单变量函数的最小值。使用方法如下：
[x, fval] = fminbnd(fun, x1, x2)
其中，fun是需要寻找最小值的函数句柄，x1和x2是定义函数最小值区间的端点。该函数将返回最小值的x和函数值fval。
3.最大值 如果要寻找函数的最大值，可以在函数前加上负号，将最大值问题转化为最小值问题。例如：
x = -fminsearch(@(x) -sin(x), 3)
该代码将寻找sin函数的最大值。
除了以上方法，MATLAB中还有其他函数和工具箱可以用于寻找最小值或最大值，如fminunc、fmincon、optimtool等。用户可以根据实际情况选择适合的方法。
九、如何进行解析几何计算，例如计算曲线和曲面的方程？
MATLAB可以通过解析几何工具箱进行解析几何计算。
1.计算曲线的方程：
（1）给定点的坐标，可以使用polyfit函数拟合曲线，得到曲线的方程。
例如，有如下的点坐标：
x = [0 1 2 3]; y = [0 2 4 6];
可以使用polyfit函数进行拟合，代码如下：
p = polyfit(x,y,2);
其中，参数x和y分别表示曲线上的点的横坐标和纵坐标，参数2表示拟合的曲线阶数，此处拟合的是一个二次曲线。
拟合得到的曲线方程为：
y = 0.7500x^2 + 0.2500x
（2）给定曲线的参数方程，可以使用fplot函数绘制曲线。
例如，要绘制圆的参数方程为：
x = cos(t); y = sin(t);
其中，t为参数。
可以使用fplot函数进行绘制，代码如下：
fplot(@(t) [cos(t),sin(t)], [0, 2*pi]);
其中，参数@(t) [cos(t),sin(t)]表示使用t计算x和y的值，[0, 2*pi]表示t的取值范围。
2.计算曲面的方程：
可以使用fit函数进行曲面拟合。
例如，有如下的点坐标：
x = [0 0 1 1; 0 0 1 1; 0 0 1 1; 0 0 1 1]; y = [0 1 0 1; 0 1 0 1; 0 1 0 1; 0 1 0 1]; z = [1 2 3 4; 2 3 4 5; 3 4 5 6; 4 5 6 7];
可以使用fit函数进行曲面拟合，代码如下：
[f, gof] = fit([x(:), y(:)], z(:), 'poly22');
其中，参数[x(:), y(:)]表示将x，y拉成一列，参数z(:)表示将z拉成一列，'poly22'表示拟合的曲面为二阶二次多项式曲面。
拟合得到的曲面方程为：
f(x,y) = 1.0505 + 1.9797x - 3.0303y + 1.0101x^2 + 1.0101y^2 - 1.0000xy
可以使用meshgrid函数生成曲面的网格，然后使用surf函数绘制曲面，代码如下：
[xq, yq] = meshgrid(0:0.1:1); zq = f(xq, yq);
surf(xq, yq, zq);
其中，[xq, yq]表示生成的网格，0
十、如何对数据进行统计分析，例如计算均值、方差、协方差等？
MATLAB是一种强大的数据分析工具，可以用其进行各种常见的统计分析，例如计算均值、方差、协方差等。以下是一些示例代码：
1.计算一个向量的平均值：
A = [1 2 3 4 5];
mean_A = mean(A);
2.计算一个向量的方差：
A = [1 2 3 4 5];
var_A = var(A);
3.计算两个向量的协方差：
A = [1 2 3 4 5];
B = [2 4 6 8 10];
cov_AB = cov(A,B);
4.计算一个矩阵的每行的平均值：
A = [1 2 3; 4 5 6; 7 8 9];
mean_A = mean(A, 2);
5.计算一个矩阵的每列的方差：
A = [1 2 3; 4 5 6; 7 8 9];
var_A = var(A, 1);
以上是一些基本的统计分析函数示例。除此之外，MATLAB还提供了其他很多用于数据分析和统计的函数，例如std、min、max等。可以查阅MATLAB的官方文档或手册来了解更多的函数和用法。
九、如何使用矩阵分解技术，例如奇异值分解和特征值分解，来解决各种数学问题？
MATLAB提供奇异值分解（SVD）和特征值分解（EVD）这两种矩阵分解技术，这些技术可用于解决各种数学问题，例如线性回归、主成分分析、图像压缩和信号处理等。
-
奇异值分解（SVD）：在MATLAB中，我们可以使用SVD函数进行奇异值分解。SVD可以将一个矩阵分解为三个矩阵的乘积：A = U * S * V'，其中U和V是正交矩阵，而S是奇异值矩阵。奇异值分解可应用于数据压缩，降维和信号处理等方面。
-
特征值分解（EVD）：MATLAB的eig函数可用于特征向量和特征值的计算。特征向量是非零向量在线性变换下仍然保持方向不变的向量，而特征值是相应的特征向量的伸缩因子。EVD可用于主成分分析，线性变换和图像处理等方面。
除了这些，MATLAB还提供其他类型的矩阵分解技术，例如QR分解和LU分解。这些技术可用于解决各种数学问题，例如线性方程组的求解和矩阵求逆等。
扫一扫
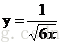
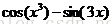
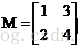
2116
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
