主成分分析 (PCA)
PCA 是一种线性降维方法,通过投影到主成分空间,尽可能保留数据的方差。
原理
PCA 通过寻找数据投影后方差最大的方向,主成分是这些方向上的正交向量。
公式推理
- 对数据中心化:
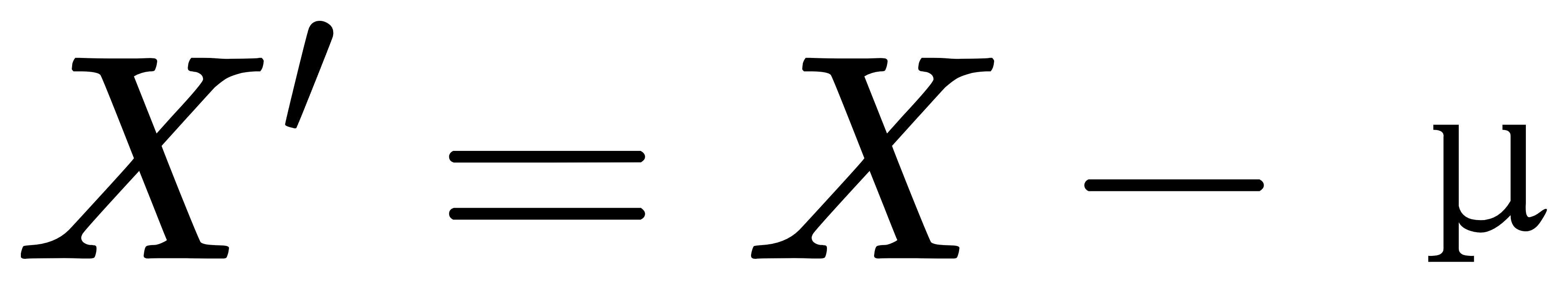
其中,μ 是数据的均值向量。
- 计算协方差矩阵:
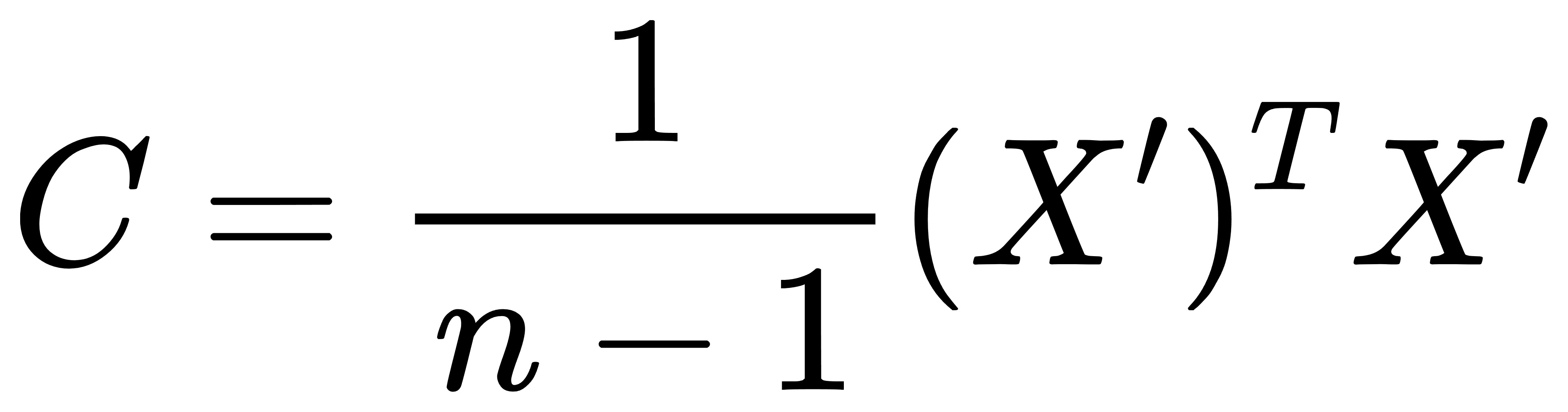
其中,n 是样本数量。
- 对协方差矩阵求特征值和特征向量:
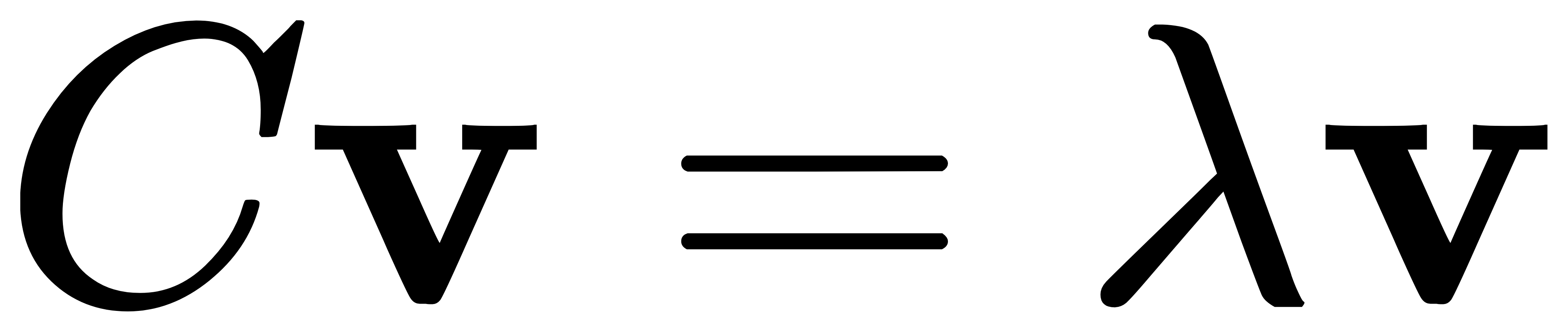
其中,v 是特征向量,λ是特征值。
- 选择前 k 个最大特征值对应的特征向量,构建投影矩阵:
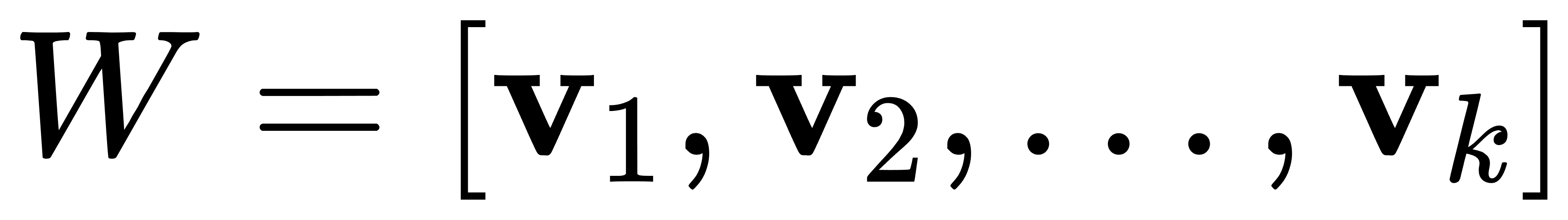
- 将原始数据投影到新的低维空间
PCA 是一种线性降维方法,通过投影到主成分空间,尽可能保留数据的方差。
PCA 通过寻找数据投影后方差最大的方向,主成分是这些方向上的正交向量。
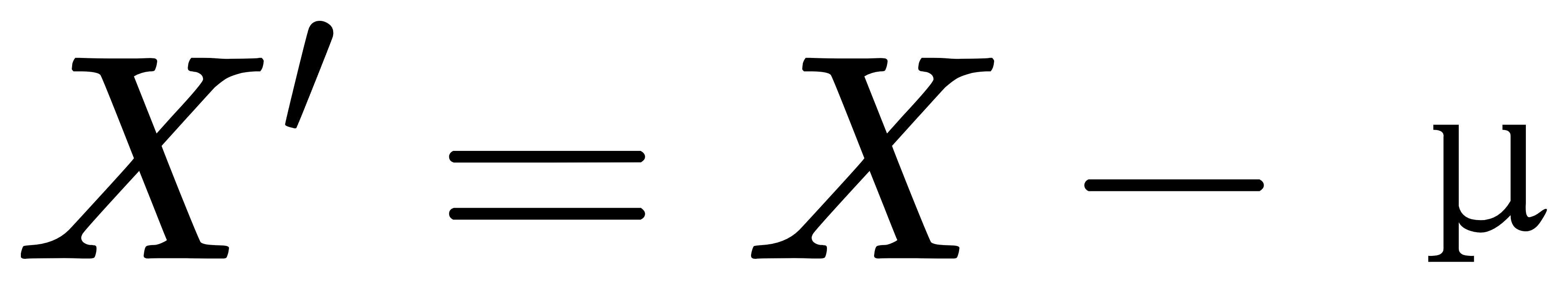
其中,μ 是数据的均值向量。
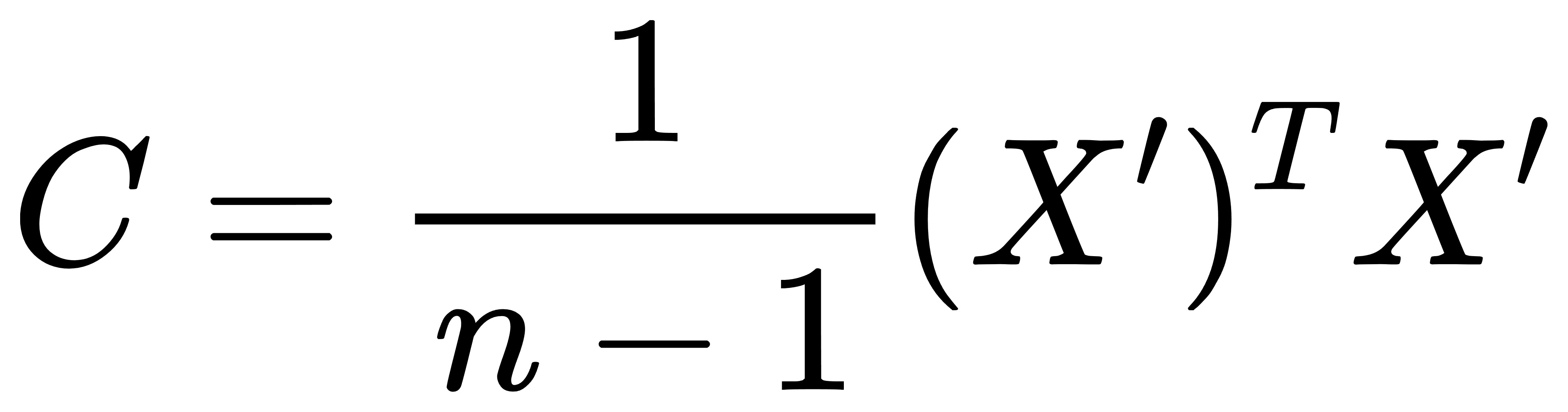
其中,n 是样本数量。
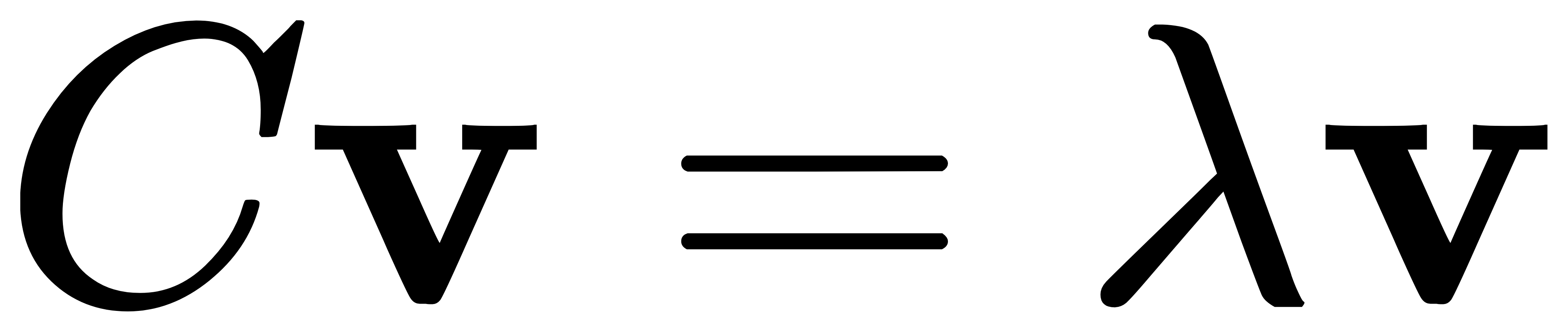
其中,v 是特征向量,λ是特征值。
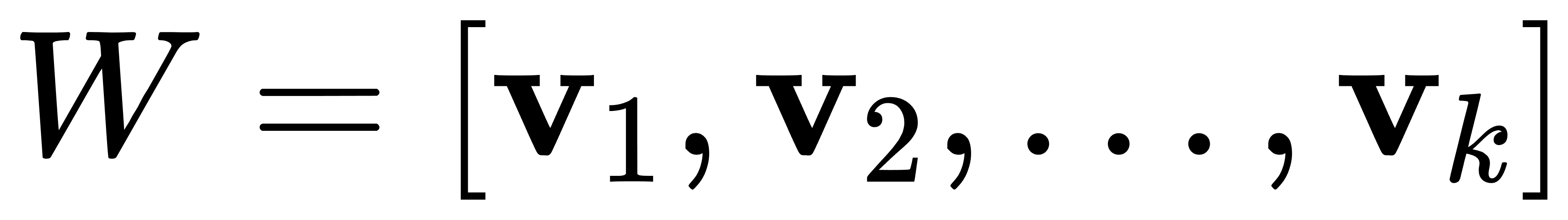
 2598
2598

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


