【C语言】递归实战——青蛙跳台（从基础到进阶）

主页链接： LSR的主页
专栏链接： 《C语言》

---

前言

今天分享的内容是递归典型问题——青蛙跳台，一起来学习一下吧。

---

一、基础版：一次跳1级或2级台阶

1.问题描述

一只青蛙要跳上n级台阶，每次只能跳 1 级或 2 级台阶，求总共有多少种不同的跳法？

2.思路分析

2.1问题分析

要计算n级台阶的跳法，需从 “最后一步” 反推：

若青蛙最后一步跳 1 级台阶，则前面需要先跳完n-1级台阶，跳法数为f(n-1)；
若青蛙最后一步跳 2 级台阶，则前面需要先跳完n-2级台阶，跳法数为f(n-2)。

2.2递推公式

因此，n级台阶的总跳法数为两种情况的和，即：
f(n) = f(n-1) + f(n-2)
这和求斐波那契数原理类似，如图所示：

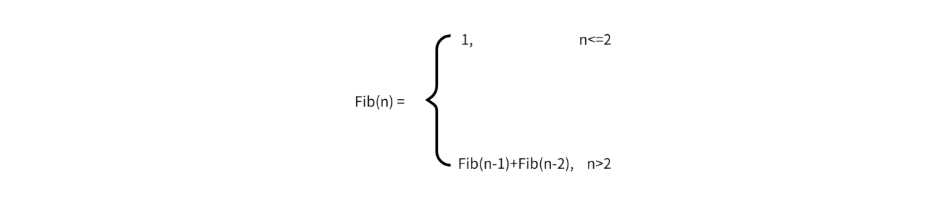
2.3边界条件

当n=1时，只有 1 种跳法（直接跳 1 级），即f(1) = 1；
当n=2时，有 2 种跳法（1+1 或直接跳 2 级），即f(2) = 2。

---

3.代码实现

3.1递归实现

// 递归实现（效率低，有重复计算）
#include <stdio.h>
int f(int n)
{
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n-1) + f(n-2);
}

int main() {
    int n = 5;
    printf("递归实现：n=%d时，跳法数=%d\n", n, f(n));
    return 0;
}

根据分析，我们可以很好的使用递归完成问题，但是和计算斐波那契数一样，会有冗杂计算，具体讲解可以移动到我之前发的函数递归中的递归与迭代：函数递归
所以我这里还是会使用迭代的方式解决这个问题。

---

3.2迭代实现

// 动态规划实现（迭代法，优化效率）
#include <stdio.h>
int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    
    int a = 1;  // f(n-2)
    int b = 2;  // f(n-1)
    int c = 0;  // f(n)
    
    for (int i = 3; i <= n; i++) {
        c = a + b;
        a = b;
        b = c;
    }
    return b;
}

int main() {
    int n = 5;
    printf("动态规划：n=%d时，跳法数=%d\n", n, f(n));
    return 0;
}

使用迭代的方法可以避免重复计算、降低时间复杂度、减少内存开销，具体在上一文（链接在递归代码结尾）有所讲解，这里就不再赘述。

---

二、进阶版：一次跳 1~k 级台阶

1.问题描述

青蛙每次可以跳 1 级、2 级…… 直到k级台阶，求跳n级台阶的总跳法数？

2.思路分析

2.1问题分析

类似基础版，最后一步可跳 1~k 级，因此总跳法为前n-1、n-2……n-k级台阶的跳法之和。

2.2递推公式

当n >= k时：f(n) = f(n-1) + f(n-2) + … + f(n-k)；
若n < k：则最后一步最多跳n级，递推公式为f(n) = f(n-1) + … + f(0)（定义f(0)=1，表示 “跳 0 级台阶有 1 种方法”）。
特殊情况：当k = n（即每次最多跳n级）时：
递推公式可简化为f(n) = 2 * f(n-1)
因为f(n) = f(n-1) + f(n-2) + … + f(0)，而f(n-1) = f(n-2) + … + f(0)，两式相减得f(n) = 2*f(n-1)。
结合f(1)=1，最终得f(n) = 2^(n-1)（如n=3时，跳法为 4 种：1+1+1、1+2、2+1、3）。

2.3边界条件

f(0) = 1（定义 “跳 0 级台阶有 1 种方法”，即不跳）；f(1) = 1（跳 1 级只有 1 种方法）

---

3.代码实现

这里使用递归的方式解决：

#include <stdio.h>

// 计算跳n级台阶（每次最多跳k级）的跳法数
int f(int n, int k) {
    if (n == 0) return 1;  // 定义：跳0级有1种方法（不跳）
    if (n == 1) return 1;
    
    int sum = 0;
    // 累加前1~k级的跳法数（若n<k则只累加前n级）
    for (int i = 1; i <= k && i <= n; i++) {
        sum += f(n - i, k);
    }
    return sum;
}

int main() {
    int n = 3, k = 3;
    printf("n=%d, k=%d时，跳法数=%d\n", n, k, f(n, k));  // 输出4
    return 0;
}

下面详细解释一下这段代码：

for (int i = 1; i <= k && i <= n; i++) {
        sum += f(n - i, k);
    }

这段代码是青蛙跳台进阶版（每次最多跳k级台阶）递归解法的核心，作用是枚举 “最后一步可能跳的台阶数”，并累加所有对应情况的跳法数。

1. 循环条件：i = 1; i <= k && i <= n; i++
   i 表示 “最后一步跳的台阶数”（从 1 开始，因为至少跳 1 级）。
   i <= k：限制最后一步最多跳k级（符合问题中 “每次最多跳k级” 的规则）。
   i <= n：当n < k时（如n=3、k=5），最后一步最多只能跳n级（不可能跳 4 级或 5 级，否则会超过总台阶数n，导致n-i为负数，无意义）。
   因此，循环的实际范围是 i 从 1 到 min(k, n)（即 “最后一步能跳的最大台阶数”）。
2. 循环体：sum += f(n - i, k)
   f(n - i, k) 表示 “跳完前面n-i级台阶的总跳法数”（因为最后一步已经跳了i级，剩下的台阶数是n-i）。
   sum 累加所有可能的情况：
   例如，当i=1时，最后一步跳 1 级，前面需跳n-1级，对应跳法数为f(n-1, k)；
   当i=2时，最后一步跳 2 级，前面需跳n-2级，对应跳法数为f(n-2, k)；
   …
   直到i达到min(k, n)，累加所有子问题的解，最终得到n级台阶的总跳法数。
   举个例子：
   假设 n=4（总台阶数），k=3（最多跳 3 级）：
   循环中i的取值为 1、2、3（因为min(3,4)=3）：

i=1：累加 f(4-1, 3) = f(3,3)（前面 3 级的跳法数）
i=2：累加 f(4-2, 3) = f(2,3)（前面 2 级的跳法数）
i=3：累加 f(4-3, 3) = f(1,3)（前面 1 级的跳法数）

最终 sum = f(3,3) + f(2,3) + f(1,3)，这就是 4 级台阶的总跳法数。

因为今天主要讲的是递归，所以进阶版的迭代方式就暂时不向大家介绍了，感兴趣可以自行了解或者等待后续。迭代思想在函数递归有所介绍。

---

总结

今天详细介绍了函数递归的具体实践方式，希望对你有所帮助。