【C语言】函数递归思想

主页链接： LSR的主页
专栏链接： 《C语言》

---

前言

关于函数递归的思想，一起来学习一下吧。

---

一、递归是什么？

通俗概括一下，递归就是函数自己调用自己。
递归的思想：
即把⼀个⼤型复杂问题层层转化为⼀个与原问题相似，但规模较⼩的⼦问题来求解；直到⼦问题不能再被拆分，递归就结束了。
那什么时候子问题才不能继续拆分呢？
这就需要我们引入限制条件，当我们递归不再满足这个限制条件时，递归就结束了。
注意：每次递归都应该往这个限制条件不断靠近。
举个例子：求n的阶乘
我们把Fact(n)当做求n的阶乘，那么Fact（n-1）就是n-1的阶乘。

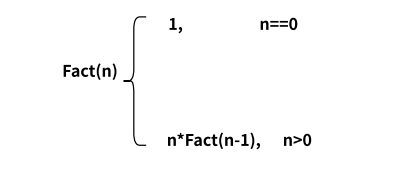
#include <stdio.h>
int Fact(int n)
{
 if(n==0)
 return 1;
 else
 return n*Fact(n-1);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fact(n);
 printf("%d\n", ret);
 return 0;
}

当我们输入n = 5时，结果就是120（此时我们不考虑n太大导致栈溢出的情况）。
这里给个图片方便你理解递归思想。

可以看到，递归思想使用的变量是非常少的，就是函数不断调用本身的一个过程。但是递归也有一定的弊端，接下来就要简单引入一个概念——栈溢出。

二、栈溢出

栈溢出（Stack Overflow）是计算机程序运行时常见的内存错误，本质是程序使用的栈内存空间超过了系统分配的最大限额，导致栈空间被耗尽的现象。
递归函数（自己调用自己）每次调用时，都会在栈上分配新的空间存储返回地址、局部变量等。如果递归次数过多（比如几万次），栈空间会被逐渐耗尽，最终导致溢出。
举个例子：

#include <stdio.h>
int main()
{
 printf("hehe\n");
 main();
 return 0;
}

栈溢出的后果：
直接后果：程序直接崩溃，通常会出现 “栈溢出错误”（如 C/C++ 中的Stack Overflow；
间接后果：可能导致程序行为异常（如数据被篡改、执行错误的代码）；
安全风险：严重时可能被恶意利用，引发安全问题（如远程代码执行）
无限递归会持续占用栈空间，超过栈容量限制导致溢出，所以在使用递归时，我们要控制递归深度，避免无限递归，必要时用循环替代递归。

---

三、递归与迭代

迭代（通常为循环），是除递归外解决问题的另一方式。
拿n的阶乘为例：

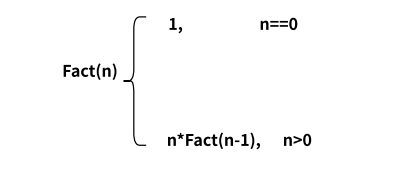
看到这个图我们很容易往递归去想：

int Fact(int n)
{
 if(n==0)
 return 1;
 else
 return n*Fact(n-1);
}

---

实际上我们用循环的方式也可以解决：

//非递归
#include <stdio.h>

int main()
{
	int n = 0;
	printf("请输入一个数：\n");
	scanf("%d", &n);
	int i = 0;
	int sum = 1;
	for (i = 1; i <= n; i++)
	{
		sum *= i;
	}
	printf("%d", sum);
	return 0;
}

---

事实上，我们看到的许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更加清晰，但是这些问题的迭代实现往往⽐递归实现效率更高。

以计算斐波那契数为例：

看到这个图片我们很容易想到使用递归的方式实现：

//计算斐波那契数列
#include <stdio.h>

int Fib(int n)
{
	int sum = 0;
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}

int main()
{
	int n = 0;
	printf("请输入一个数:");
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
	return 0;
}

但是这种方式是非常冗余的，我们可以测试一下：

#include <stdio.h>
int count = 0;
int Fib(int n)
{
 if(n == 5)
 count++;//统计第5个斐波那契数被计算的次数
 if(n<=2)
 return 1;
 else
 return Fib(n-1)+Fib(n-2);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fib(n);
 printf("%d\n", ret); 
 printf("\ncount = %d\n", count);
 return 0;
}

这⾥我们看到了，在计算第30个斐波那契数的时候，使⽤递归方式，第5个斐波那契数就被重复计算了121393次，这些计算是非常冗余的。所以斐波那契数的计算，使⽤递归是非常不明智的，我们就得想迭代的方式解决。
我们知道前两个斐波那契数都是1，前两个数相加就是第三个数，以此类推：

int Fib(int n)
{
 int a = 1;
 int b = 1;
 int c = 1;
 while(n>2)
 {
 c = a+b;
 a = b;
 b = c;
 n--;
 }
 return c;
}

这样效率就高了很多。

---

总结

递归是函数调用自身的过程，通过将大问题分解为相似的子问题来解决。
递归可能引发栈溢出错误，所以要根据实际问题在递归和迭代之中取舍。
以上就是今天分享的递归内容，希望可以帮助到你。