Leetcode48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

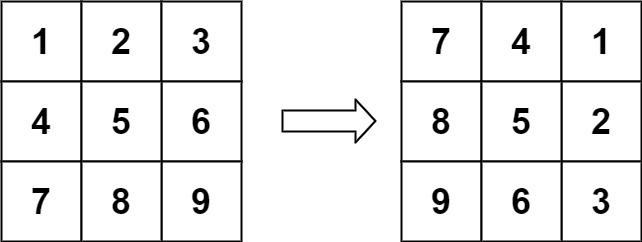
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

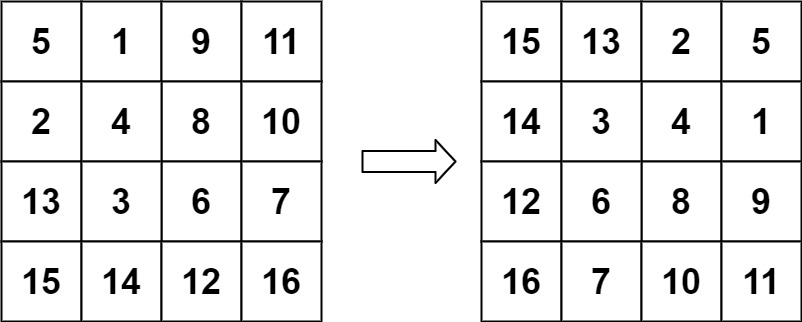
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000  

思路：先水平折中反转，然后沿主对角线反转，看详细注释，图出之Leetcode

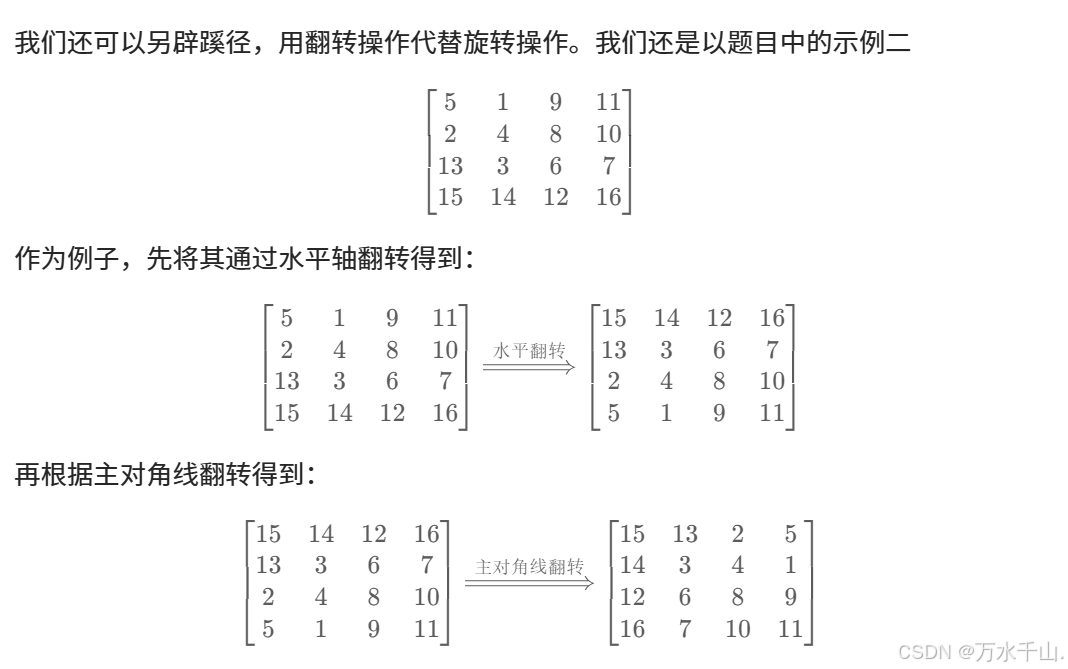
代码：

class Solution {
    public void rotate(int[][] matrix) {
        //矩阵一定为是一个行和列数量相等的矩阵
        //计算行和列
        int n = matrix.length;
        int temp = 0;
        //i<n/2,是因为在反转时我们是需要交换上一半的矩阵就行了，
        //交换的时候下半矩阵也自然交换
        for(int i = 0;i < n/2;i++) {
            for(int j = 0;j < n;j++){
                temp = matrix[i][j];
                //交换的行坐标相加等于行数减一，可以自己算算
                //所以需要交换的行为n-i-1，列坐标不变
                matrix[i][j] =  matrix[n - i -1][j];
                matrix[n - i -1][j] = temp;
            }
        }

        //主对角线反转，同样只需要实现沿主对角线分割的一半矩阵即可
        //右上对角的矩阵的特性就是列坐标小于行坐标
        for(int i = 0;i < n;i++){
            for(int j = 0;j < i;j++){
                temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}