线性规划-单纯形法推导

最新推荐文章于 2025-03-24 14:31:48 发布

原创最新推荐文章于 2025-03-24 14:31:48 发布 · 1.3k 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#数学建模

这里写目录标题

线性规划例子
- 啤酒厂问题
- 图解法
单纯形法数学推导
- 将问题标准化并转为矩阵形式
- 开始推导
实例
- 图解法
- 单纯形法

线性规划例子

啤酒厂问题

每日销售上限：100箱啤酒
营业时间：14小时
生产1箱生啤需1小时
生产1箱黑啤需2小时
生啤售价：20美元/箱
黑啤售价：30美元/箱

目标：最大化利润

我们可以根据上述描述，建立数学模型。假设生啤生产 $x_1$ 箱，黑啤生产 $x_2$ 箱，那么就有如下的线性规划式子。
$Max_{x_1,x_2} \qquad20 \times x_1 + 30 \times x_2 \\ \qquad s.t. \qquad \qquad x_1 + 2\times x_2<=14 \\\qquad \qquad \qquad x_1+x_2<=100 \\\qquad \qquad \qquad x_1,x_2>=0$

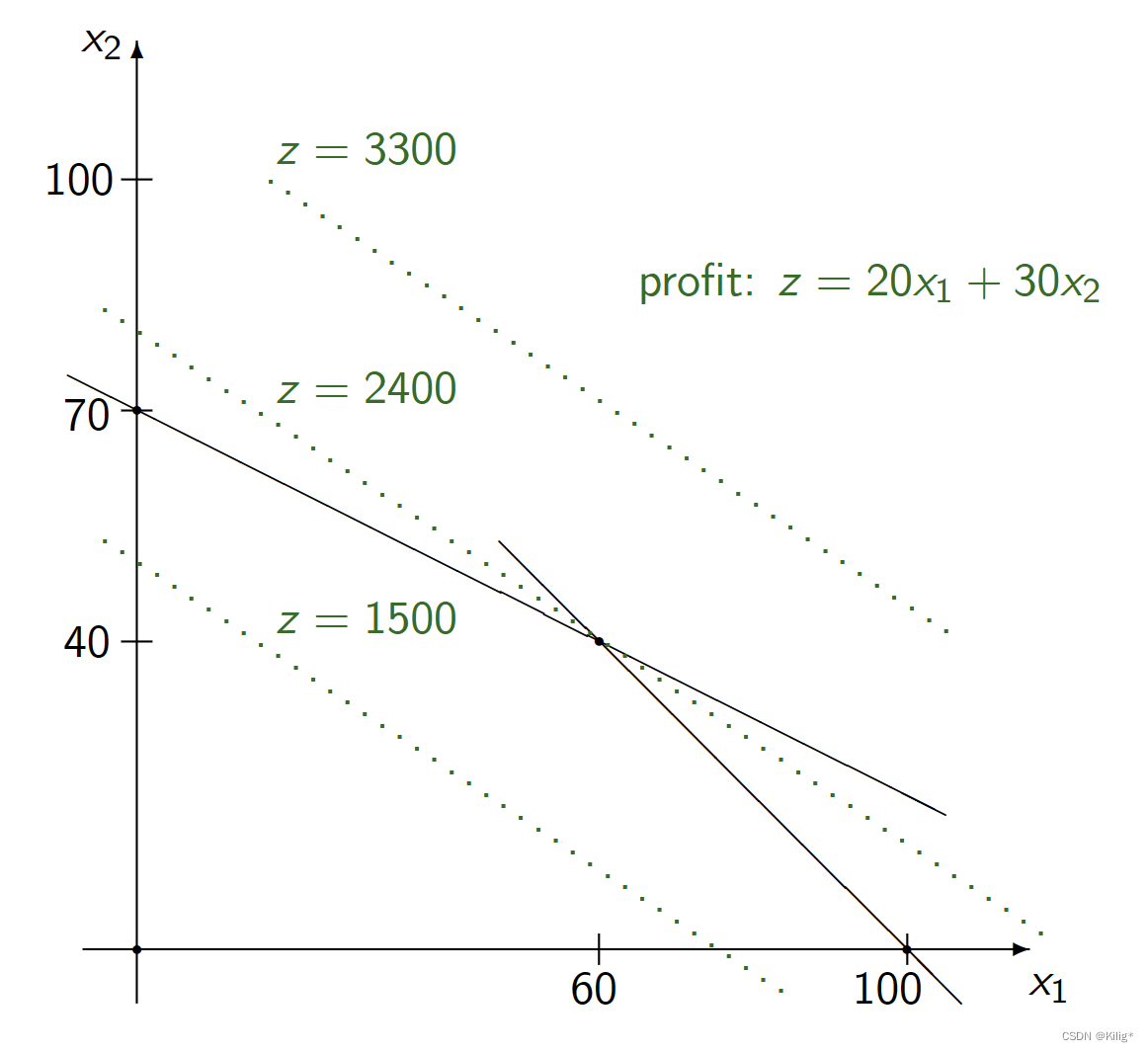
图解法

通过求解上述的线性规划问题即可得到最优的生产计划。那么如何求解呢？根据图解法可以看出最优值为2400。而且可以观察到随着z的上下平移，最终取到的最优值必定是z与凸多边形（约束域）的某一个顶点相交得到。这样的话如果想求解一个线性规划问题，只需要遍历这个凸多边形（在高维空间中是凸多面体）的每一个顶点，对目标函数值大小进行比较即可。
在这里插入图片描述

单纯形法数学推导

将问题标准化并转为矩阵形式

那么如何将遍历各个顶点的过程转化为数学语言来表述呢，且是否真的需要将所有顶点遍历一遍，有没有更高效的遍历方法？

还是上述的问题，我们可以把问题先化为标准型再写成矩阵形式。
标准型：
$Min_{x_1,x_2} \qquad-20 \times x_1 - 30 \times x_2 \\ \qquad s.t. \qquad \qquad x_1 + 2\times x_2 + x_3=14 \\\qquad \qquad \qquad x_1+x_2 + x_4 =100 \\\qquad \qquad \qquad x_1,x_2,x_3,x_4>=0$

这个问题的矩阵形式为：
$\text{Minimize} \quad \mathbf{c}^\top \mathbf{x}\\ \text{Subject to:} \quad \mathbf{Ax} = \mathbf{b} \quad \text{and} \quad \mathbf{x} \geq \mathbf{0}$

其中：

$\mathbf{c} = \begin{bmatrix} -20 \\ -30 \\ 0 \\ 0 \\ \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} 14 \\ 100 \\ \end{bmatrix}$

约束矩阵 $\mathbf{A}$ 为：

$\mathbf{A} = \begin{bmatrix} 1 & 2 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ \end{bmatrix}$
这里的变量 $x_3$ 和 $x_4$ 是松弛变量，用于将不等式约束转换为等式约束。

开始推导

令 $x = [x_B,x_N],A = [B,N],c = [c_B,c_N]^T$ (注意这里的B一定要是一个可逆矩阵),初始化时令 $x_N$ 全为0.
那么原问题可以转化为如下形式
$\qquad c_B\times x_B + c_N\times x_N \\ s.t.\qquad \qquad \qquad B\times x_B + N\times x_N = b \\ \qquad \qquad \qquad x_B>=0,x_N>=0$
将约束条件 $B\times x_B + N\times x_N = b$ 可以等价变形为 $x_B = B^{-1}(b - N\times x_N) = B^{-1}b$
注意：上面用到了 $B^{-1}$ ，这也是为什么说B得是可逆矩阵的原因,在后面的转化还用到了 $x_N$ 初始全为0。

将变换之后的式子带回目标函数 $c_B\times x_B + c_N\times x_N$ 就有 $c_B\times B^{-1}(b - N\times x_N) + c_N\times x_N$ ,进一步化简可以得到如下式子（由于在初始化时 $x_N$ 全为0）
$c_BB^{-1}b +(c_N - c_BB^{-1}N)x_N = c_BB^{-1}b$
可以观察到，目标函数还有进一步变小的可能，那就是 $c_N - c_BB^{-1}N)x_N$ 之前由于 $x_N$ 全为0，所以这一项也为0，但如果 $x_N$ 中某一项的系数为负，将该项从0变为非0即可进一步减小目标函数。那么如何变更高效呢？就是找到负系数中，负系数绝对值最大的那一项（在x变化量一致的情况下，负系数绝对值越大，目标函数值下降的就越多）。

那么也可以推出，如果 $c_N - c_BB^{-1}N)$ 全部为正，即使将 $x_N$ 的任意一项由0变为非0，目标函数值也不会降低，这时就可以说已经找到了目标函数的最小值，这也是算法的收敛准则: $c_N - c_BB^{-1}N)>=0$ 。

那么假如 $c_N - c_BB^{-1}N)_i$ 是负系数中系数绝对值最大的的那一项，对应这一项的变量为 $x_{N_{i}}$ ,我们要将其由0变为非0，那么要变为多少呢？
注意到对于 $x_B$ 还有 $x_B>=0$ 的约束。且有 $x_B = B^{-1}(b - N\times x_N)$ ， $x_N$ 的变化也会引起 $x_B$ 的变化，我们应该使变化之后的 $x_B$ 仍然满足非负性。在 $x_B>=0$ 的情况下， $x_N$ 要变得尽可能大。那么就有如下式子：
$B^{-1}(b - N\times x_N)>=0 \\b - N\times x_N>=0 \\$
为了满足上述式子，而 $x_{N_{i}}$ 变得又要尽可能多，那么 $x_{N_{i}} = min\{\frac{b}{N} \} = \frac{b_j}{N_j}$ ,这样的话同时就把 $x_{B_j}$ 变为0.
如此就完成了一轮迭代，不断迭代知道达到收敛准则为止。迭代的过程其实也是从一个端点替换到另一个端点的过程。

实例

对于线性规划问题
$\qquad 2x_1 + 3x_2 \\s.t. \qquad 4x_1 + x_2<=16 \\ \qquad -x_1+x_2<=6 \\ \qquad x_1,x_2>=0$

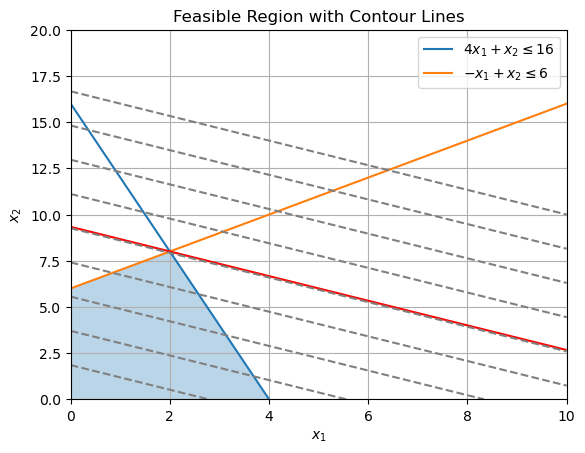
图解法

利用图解法可以看到红色的线是最优的等值线， $x_1 = 2,x_2 = 8$ .
在这里插入图片描述

单纯形法

将原来的线性规划化为标准型并写为矩阵形式
$\qquad -2x_1 - 3x_2 \\s.t. \qquad 4x_1 + x_2+x_3=16 \\ \qquad -x_1+x_2+x_4=6 \\ \qquad x_1,x_2,x_3,x_4>=0$
其中， $x_3$ 和 $x_4$ 是松弛变量。

矩阵形式为：

目标函数： $\text{Maximize} \quad \mathbf{c}^\top \mathbf{x}$
其中， $\mathbf{c} = \begin{bmatrix} -2 \\ -3 \\ 0 \\ 0 \end{bmatrix}$ 为目标函数的系数向量。

约束条件： $\mathbf{Ax} = \mathbf{b}$ ，其中 $\mathbf{A} = \begin{bmatrix} 4 & 1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{bmatrix}$ 是约束系数矩阵， $\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}$ 是决策变量向量， $\mathbf{b} = \begin{bmatrix} 16 \\ 6 \end{bmatrix}$ 是约束右端项向量。
因此，标准型的线性规划问题可以表示为：
$\begin{align*} \text{Maximize} \quad & \mathbf{c}^\top \mathbf{x} \\ \text{Subject to} \quad & \mathbf{Ax} = \mathbf{b} \\ & \mathbf{x} \geq 0 \end{align*}$
那么根据上述单纯形法的推导， $x_B = [x_3,x_4],x_N = [x_1,x_2],N = \begin{bmatrix} 4 & 1 \\ -1 & 1 \end{bmatrix},B = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},c_B = [0,0],c_N = [-2,-3]$
初始时令 $x_N = [0,0]$
第一轮迭代：
此时 $c_N - c_BB^{-1}N = [-2,-3]$ 因此选择 $x_2$ 作为入基变量更为高效，且 $Nx_N =\begin{bmatrix} 16 - 4x_1 - x_2 \\ 6 +x_1-x_2 \end{bmatrix}>=0$ 故 $x_2 = 6$ 并令 $x_4 = 0$ , $x_2$ 入基, $x_4$ 出基.
经过此轮迭代后，各变量如下
$x_B = [x_3,x_2],x_N = [x_1,x_4],N = \begin{bmatrix} 4 & 0 \\ -1 & 1 \end{bmatrix},B = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix},c_B = [0,-3],c_N = [-2,0]$
第二轮迭代:
此时 $c_N - c_BB^{-1}N = [-5,3]$ ,选择 $x_1$ 作为入基变量更为高效，且 $Nx_N =\begin{bmatrix} 16 - 4x_1 \\ 6 +x_1 \end{bmatrix}>=0$ 故 $x_1 = 4$ 并令 $x_3 = 0$ , $x_1$ 入基, $x_3$ 出基.
经过此轮迭代后，各变量如下
$x_B = [x_1,x_2],x_N = [x_3,x_4],N = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},B = \begin{bmatrix} 4 & 1 \\ -1 & 1 \end{bmatrix},c_B = [-2,-3],c_N = [0,0]$
第三轮迭代:
此时 $c_N - c_BB^{-1}N = [1,2]$ 都大于0，达到收敛条件，此时令 $x_N = [0,0]$ 解得 $x_B = [2,8]$ 最小值为28.

附：图解法绘图代码

import numpy as np
import matplotlib.pyplot as plt

# 定义约束条件
x = np.linspace(0, 10, 400)  # 创建x轴的值
eq1 = 16 - 4*x  # 约束条件1: 4x1 + x2 <= 16 => x2 <= 16 - 4x1
eq2 = 6 + x  # 约束条件2: -x1 + x2 <= 6 => x2 >= -x1 + 6

# 画出约束条件
plt.plot(x, eq1, label=r'$4x_1 + x_2 \leq 16$')
plt.plot(x, eq2, label=r'$-x_1 + x_2 \leq 6$')
plt.xlim((0, 10))
plt.ylim((0, 20))
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')

# 标记可行域
plt.fill_between(x, np.minimum(eq1, eq2), where=(eq1 >= 0) & (eq2 >= 0), alpha=0.3)

# 添加等值线
x_vals = np.linspace(0, 10, 100)
y_vals = np.linspace(0, 20, 100)
X, Y = np.meshgrid(x_vals, y_vals)
Z = 2*X + 3*Y
max_val = np.max(Z)

# 调整等值线范围
plt.contour(X, Y, Z, levels=[28], colors='red')
plt.contour(X, Y, Z, levels=np.linspace(0, 50, 10), colors='grey', linestyles='dashed')

# 添加标签和图例
plt.title('Feasible Region with Contour Lines')
plt.legend()
plt.grid(True)
plt.show()