划艇比赛的成绩（复习题）

1.2 划艇比赛的成绩（复习题）

题目来源:《数学模型》（第五版）–姜启源、谢金星、叶俊

1.2.1 题目描述

已知各种赛艇的比赛成绩和规格

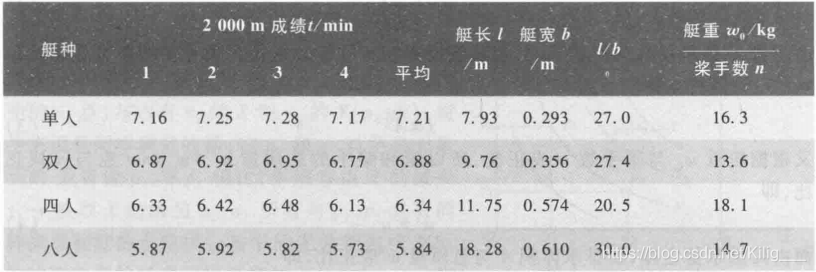
问题 :考虑八人艇分重量级组（桨手体重不超过86kg）和轻量级组（桨手体重不超过73kg），建立模型说明重量级组的成绩比轻量级组的成绩好大约5%。

1.2.2 问题分析

船在水中行驶会受到比赛队员划桨浆的推力和水对船的阻力，比赛队员越健壮，队员人数越多，能够给船提供的动力就越大。但同时船和队员的总重量越大，船的浸没面积增大，阻力也会增大。

1.2.3 模型假设

1. 船速$v$是常数，前进时受到的阻力$f$与$s{v}^2$成正比（$s$是船浸没部分的面积）
2. 所有浆手体重都相同，且都为当前重量级的最大体重，记为$w$;在比赛中每个比赛选手的划桨功率$p$保持不变，且$p$与$w$成正比。
3. 各种艇的几何形状相同，$l/b$为常数；艇重与浆手数$n$和浆手平均体重$w$成正比。

对于假设1，物理学中本就有$f\propto v^2$的情况，对于假设2，$w,p$常数属于必要的简化而$p$与$w$成正比可解释为:$p$与肌肉体积、肺的体积成正比，对于身材匀称的运动员，肌肉、肺的体积与体重$w$成正比。

1.2.4 模型

有$n$名浆手的船的总功率$np$与阻力$f$和速度$v$的乘机成正比（如果船保持匀速运动的话，单位时间内浆手对船做的功$=$单位时间内阻力做的功）即有$$np\propto fv$$由假设1,2可以得到$f\propto s{v}^2$,$p\propto w$。
带入式中即可化简得到
$$nw\propto s{v}^3$$由于题目中已经固定艇为8人艇，故$n=8$为常数。故有$$v\propto ($$