Leetcode（76）——最小覆盖子串

原创已于 2022-06-29 12:40:20 修改 · 2.6k 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构

于 2022-06-29 12:39:52 首次发布

Leetcode 专栏收录该内容

77 篇文章

订阅专栏

本文介绍了如何使用滑动窗口算法解决LeetCode第76题——最小覆盖子串。通过维护一个哈希表来跟踪目标字符串所需字符的出现次数，不断移动窗口边界来找到包含所有目标字符的最小子串。文章详细分析了算法的优化过程，从最初的版本到最终的优化版本，逐步减少了不必要的操作，实现了线性时间复杂度的解决方案。

Leetcode（76）——最小覆盖子串

题目

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”

示例 2：

输入：s = “a”, t = “a”
输出：“a”

示例 3：

输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

$1$ <= s.length, t.length <= $10^5$
s 和 t 由英文字母组成

进阶：你能设计一个在 $O (n)$ 时间内解决此问题的算法吗？

题解

方法一滑动窗口：

思路

滑动窗口可用于解决一些列的字符匹配问题，典型的问题包括：在字符串 $s$ 中找到一个最短的子串，使得其能覆盖到目标字符串 $t$ 。对于目标字符串 $t$ ，我们可以在字符串 $s$ 上滑动窗口，当窗口包含 $t$ 中的全部字符后，我们再根据题意考虑能否收缩窗口。
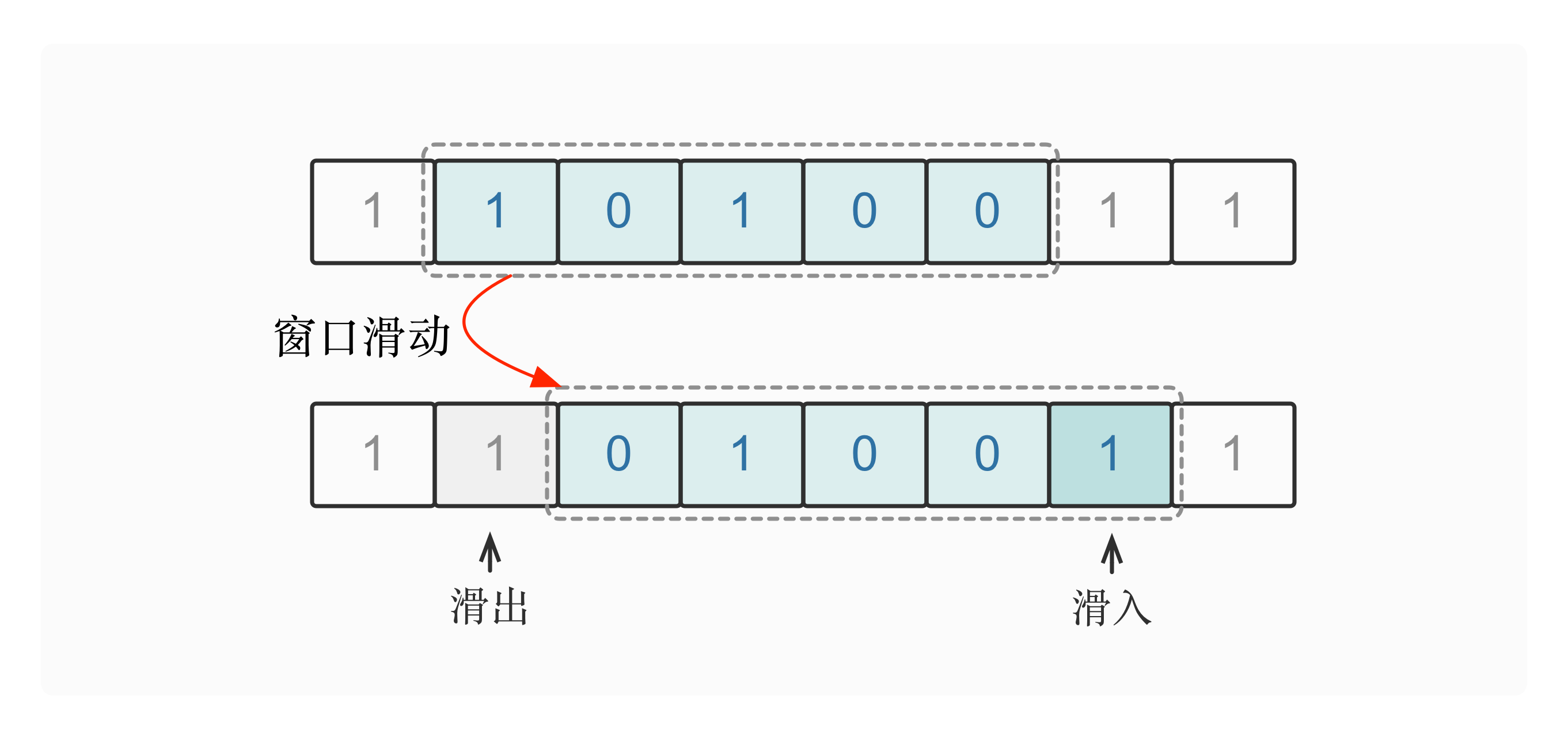
在窗口滑动的过程中，我们可以暴力地统计出窗口中所包含的字符是否满足题目要求，但这没有利用到滑动窗口的基本性质。事实上，窗口的滑动过程可分解为以下两步基础操作：

窗口右边界往右滑动一位：窗口右端新加入一个字符，但窗口中的其他字符没有发生变化；
窗口左边界往右滑动一位：窗口左端滑出一个字符，但窗口中的其他字符没有发生变化。

因此，我们可以考虑在「一进一出」这样的两个基础操作上做文章。

在这里插入图片描述

而本问题要求我们返回字符串 $s$ 中包含字符串 $t$ 的全部字符的最小窗口。我们称包含 $t$ 的全部字母的窗口为「可行」窗口。
我们可以用滑动窗口的思想解决这个问题。在滑动窗口类型的问题中都会有两个指针，一个用于「延伸」现有窗口的 $r$ 指针，和一个用于「收缩」窗口的 $l$ 指针。在任意时刻，只有一个指针运动，而另一个保持静止。我们在 $s$ 上滑动窗口，通过移动 $r$ 指针不断扩张窗口。当窗口包含 $t$ 全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

在这里插入图片描述

如何判断当前的窗口包含所有 $t$ 所需的字符呢？
我们可以用一个哈希表表示 $t$ 中所有的字符以及它们的现有个数（等于0表示刚好满足需求数，大于0表示缺少，小于0表示超出），用一个哈希表动态维护窗口中所有的字符以及它们的个数，如果这个动态表中包含 $t$ 的哈希表中的所有字符，并且对应的个数都不小于 $t$ 的哈希表中各个字符的个数，那么当前的窗口是「可行」的。

注意：这里 $t$ 中可能出现重复的字符，所以我们要记录字符的个数。

考虑如何优化？
如果 ${\rm XX \cdots XABCXXXX}$ ， ${\rm ABC}$ ，那么显然 $[XX⋯XABC]{\rm [XX \cdots XABC]}$ 是第一个得到的「可行」区间，得到这个可行区间后，我们按照「收缩」窗口的原则更新左边界，得到最小区间。我们其实做了一些无用的操作，就是更新右边界的时候「延伸」进了很多无用的 $X\rm X$ ，更新左边界的时候「收缩」扔掉了这些无用的 $X\rm X$ ，做了这么多无用的操作，只是为了得到短短的 $ABC\rm ABC$ 。没错，其实在 $s$ 中，有的字符我们是不关心的，我们只关心 $t$ 中出现的字符，我们可不可以先预处理 $s$ ，扔掉那些 $t$ 中没有出现的字符，然后再做滑动窗口呢？也许你会说，这样可能出现 $XXABXXC\rm XXABXXC$ 的情况，在统计长度的时候可以扔掉前两个 $X\rm X$ ，但是不扔掉中间的 $X\rm X$ ，怎样解决这个问题呢？优化后的时空复杂度又是多少？
优化方法：在遍历时找到 $t$ 中第一个属于 $t$ 字符，并令它为滑动窗口的 head。当 num=0 时，说明找到了一个满足题意的窗口使得中的字符能够覆盖 t 中的全部字符。此时需要更新 head 以除去多余的字符，因为结尾字符一定是需求字符且其个数等于需求总数，只需要更新 head 即可

代码实现

我的初始版本：

class Solution {
public:
    string minWindow(string s, string t) {
        if(s.size() < t.size()) return "";
        unordered_map<char, pair<int, int>> hash;  // <字符,<需求总数,滑动窗口现有总数>>
        for(auto& it: t){
            if(hash.count(it) == 0){
                hash[it].first = 1;
                hash[it].second = 0;
            }else hash[it].first++;
        }
        // 最小子串的头尾和长度，当前子串的头和尾，遍历的指针，当前窗口中未存在的字符个数
        int min_head, min_l, head, ptr, num, size;
        head = ptr = 0;
        num = t.size();
        size = s.size();
        min_l = size + 1;
        while(ptr < size){
            if(hash.count(s[ptr]) != 0){
                hash[s[ptr]].second++;  // 更新该字符的滑动窗口现有总数
                if(hash[s[ptr]].second <= hash[s[ptr]].first) num--;
                if(num == 0){
                    /*
                    如果遇到某个字符的滑动窗口现有总数 > 需求总数，保证头字符 hash[s[head]].second == hash[s[head]].first
                    则更新 head 。更新 head 时，从 head 一直更新到 s 中的某个字符的滑动窗口现有总数等于需求总数
                    并且将该字符的下标作为新的 head
                    */
                    while(true){
                        // 滑动窗口中的每个字符的滑动窗口现有总数一定是大于等于其需求总数
                        if(hash.count(s[head]) != 0){
                            if(hash[s[head]].second == hash[s[head]].first) break;
                            else hash[s[head]].second--;    // 大于其需求总数
                        }
                        head++;
                    }
                    if(ptr-head+1 < min_l){
                        min_l = ptr-head+1;
                        min_head = head;
                    }
                }
            }
            ptr++;
        }
        return min_l > size? "": s.substr(min_head, min_l);
    }
};

我的改进版本（优化哈希表的定义）：

class Solution {
public:
    string minWindow(string s, string t) {
        if(s.size() < t.size()) return "";
        unordered_map<char, int> hash;  // <字符, 滑动窗口对该字符需求数(0表示等于需求总数，大于0表示还缺少，小于0表示超出)> 
        for(auto& it: t){
            if(hash.count(it) == 0) hash[it] = 1;
            else hash[it]++;
        }
        // 最小子串的头尾和长度，当前子串的头和尾，遍历的指针，当前窗口中未存在的字符个数
        int min_head, min_l, head, ptr, num, size;
        head = ptr = 0;
        num = t.size();
        size = s.size();
        min_l = size + 1;
        while(ptr < size){
            if(hash.count(s[ptr]) != 0){
                hash[s[ptr]]--;  // 更新该字符的滑动窗口现有总数
                if(hash[s[ptr]] >= 0) num--;
                if(num == 0){
                    /*
                    如果遇到某个字符的滑动窗口现有总数 > 需求总数，保证头字符 hash[s[head]].second == hash[s[head]].first
                    则更新 head 。更新 head 时，从 head 一直更新到 s 中的某个字符的滑动窗口现有总数等于需求总数
                    并且将该字符的下标作为新的 head
                    */
                    while(true){
                        // 滑动窗口中的每个字符的滑动窗口现有总数一定是大于等于其需求总数
                        if(hash.count(s[head]) != 0){
                            if(hash[s[head]] == 0) break;
                            else hash[s[head]]++;    // 大于其需求总数
                        }
                        head++;
                    }
                    if(ptr-head+1 < min_l){
                        min_l = ptr-head+1;
                        min_head = head;
                    }
                }
            }
            ptr++;
        }
        return min_l > size? "": s.substr(min_head, min_l);
    }
};

我的最终改进版本（优化内层循环）：

class Solution {
public:
    string minWindow(string s, string t) {
        if(s.size() < t.size()) return "";
        unordered_map<char, int> hash;  // <字符, 滑动窗口对该字符需求数(0表示等于需求总数，大于0表示还缺少，小于0表示超出)> 
        for(auto& it: t){
            if(hash.count(it) == 0) hash[it] = 1;
            else ++hash[it];
        }
        // 最小子串的头尾和长度，当前子串的头和尾，遍历的指针，当前窗口中未存在的字符个数
        int min_head, min_l, head, ptr, num, size;
        head = ptr = 0;
        num = t.size();
        size = s.size();
        min_l = size + 1;
        while(ptr < size){
            if(hash.count(s[ptr]) != 0){
                // 更新该字符的滑动窗口现有总数 --hash[s[ptr]]
                if(--hash[s[ptr]] >= 0) num--;
                // 当 num=0 时，说明找到了一个满足题意的窗口使得中的字符能够覆盖 t 中的全部字符
                // 此时需要更新 head 以除去多余的字符，因为结尾字符一定是需求字符且其个数等于需求总数，只需要更新 head 即可
                while(num == 0){
                    if(ptr-head+1 < min_l){
                        min_l = ptr-head+1;
                        min_head = head;
                    }
                    // 滑动窗口中的每个字符的滑动窗口现有总数一定是大于等于其需求总数
                    // 判断减去当前字符后，是否还满足其在滑动窗口现有总数不少于其需求总数的要求
                    if(hash.count(s[head]) != 0 && ++hash[s[head]] > 0) num++;
                    head++;
                }
            }
            ptr++;
        }
        return min_l > size? "": s.substr(min_head, min_l);
    }
};

Leetcode 官方题解：

class Solution {
public:
    string minWindow(string s, string t) {
        vector<int> chars(128, 0);
        vector<bool> flag(128, false);
        // 先统计T中的字符情况
        for(int i = 0; i < t.size(); ++i) {
            flag[t[i]] = true;
            ++chars[t[i]];
        }
        // 移动滑动窗口，不断更改统计数据
        int cnt = 0, l = 0, min_l = 0, min_size = s.size() + 1;
        for (int r = 0; r < s.size(); ++r) {
            if (flag[s[r]]) {
                if (--chars[s[r]] >= 0) {
                ++cnt;
                }
                // 若目前滑动窗口已包含T中全部字符，
                // 则尝试将l右移，在不影响结果的情况下获得最短子字符串
                while (cnt == t.size()) {
                    if (r - l + 1 < min_size) {
                        min_l = l;
                        min_size = r - l + 1;
                    }
                    if (flag[s[l]] && ++chars[s[l]] > 0) {
                        --cnt;
                    }
                    ++l;
                }
            }
        }
        return min_size > s.size()? "": s.substr(min_l, min_size);
    }
};

网友优解：

class Solution {
public:
    string minWindow(string s, string t) {
        int hash[128] = {0};
        for (auto& c : t) {
            ++hash[c];
        }
        int count[128] = {0};
        int cnt = 0;
        int beg = 0;
        int min_len = INT_MAX;
        int min_beg = 0;
        for (int i = 0; i < s.size(); ++i) {
            char c = s[i];
            if (hash[c]) {
                ++count[c];
                if (count[c] <= hash[c]) {
                    ++cnt;
                }
            }
            if (cnt == t.size()) {
                for (; beg < i; ++beg) {
                    char nc = s[beg];
                    if (hash[nc]) {
                        if (count[nc] > hash[nc]) {
                            --count[nc];
                            continue;
                        }
                        break;
                    }
                }
                int len = i - beg + 1;
                if (len < min_len) {
                    min_len = len;
                    min_beg = beg;
                }
            }
        }
        return min_len == INT_MAX? "" : s.substr(min_beg, min_len);
    }
};

复杂度分析

初始版本的代码分析：
时间复杂度：最坏情况下左右指针对 $s$ 的每个元素各遍历一遍，哈希表中对 $s$ 中的每个元素各插入、删除一次，对 $t$ 中的元素各插入一次。每次检查是否可行会遍历整个 $t$ 的哈希表，哈希表的大小与字符集的大小有关，设字符集大小为 $C$ ，则渐进时间复杂度为 $O(C⋅∣s∣+∣t∣)O(C\cdot |s| + |t|)$ 。
空间复杂度：这里用了两张哈希表和多个临时变量作为辅助空间，每个哈希表最多不会存放超过字符集大小的键值对，我们设字符集大小为 $C$ ，则渐进空间复杂度为 $O (C)$

改进版本的代码分析：
时间复杂度： $O (n)$ ， $n$ 指字符串 $s$ 的长度。虽然在 for 循环里嵌套了一个 while 循环，但是因为 while 循环负责移动 $p t r$ 指针，且 $p t r$ 只会从左到右移动一次，因此总时间复杂度仍然是 $O (n)$ 。
空间复杂度：这里用了一张哈希表和多个临时变量作为辅助空间，每个哈希表最多不会存放超过字符集大小的键值对，我们设字符集大小为 $C$ ，则渐进空间复杂度为 $O (C)$