概率论-事件的概率--公理化定义（统计、古典、几何）

一、公理化定义
即概率的:统计定义、古典定义、几何定义
二、统计定义
1.定义

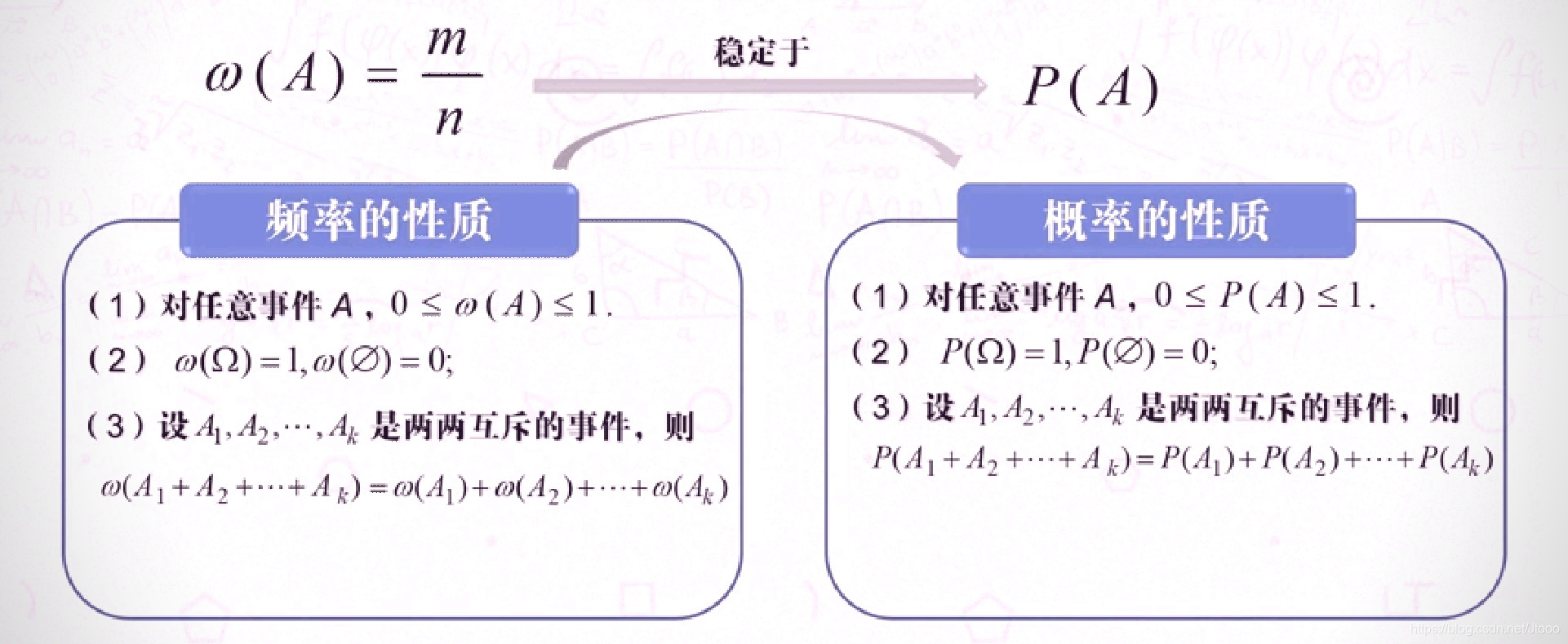
注:其中（3）运用的是概率的有限可加性
（4）
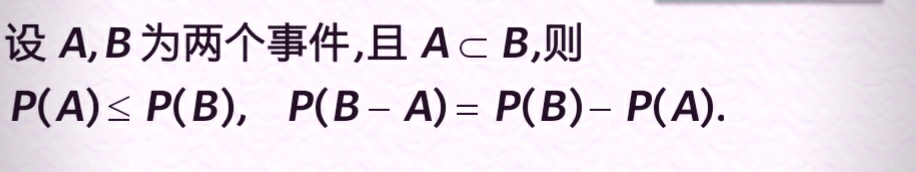
（5）

2.
优点：直观，适用于未知情况
缺点：大量重复试验，不便于实际运用；不够严谨精确，不便于理论运用。

三、古典定义：（有限性、等可能性）
例题：
补充：




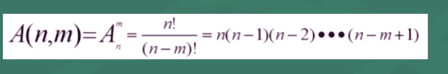
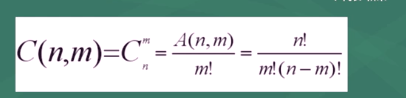
例：
A(4,2)=4!/2!=4·3=12
C(4,2)=4!/(2!·2!)=4·3/(2·1)=6

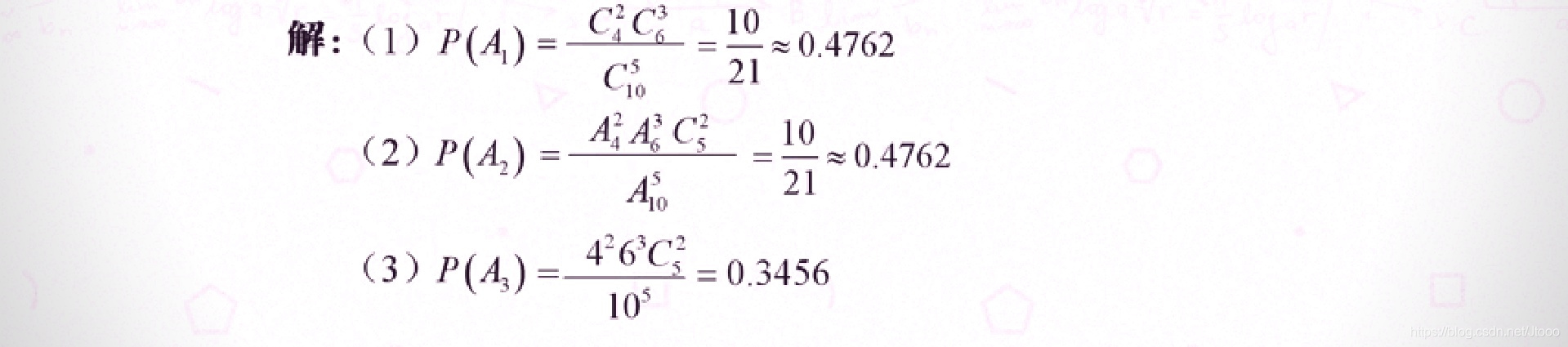
古典概型的基本模型一、:摸球模型
(1) 无放回地摸球

问题1： 设袋中有4 只白球和 2只黑球, 现从袋中无
放回地依次摸出2只球,求这2只球都是白球的概率.
(2) 有放回地摸球
问题2 设袋中有4只红球和6只黑球,现从袋中有放
回地摸球3次,求前2次摸到黑球、第3次摸到红球
的概率.
古典概型的基本模型二：球放入杯子模型
(1)杯子容量无限
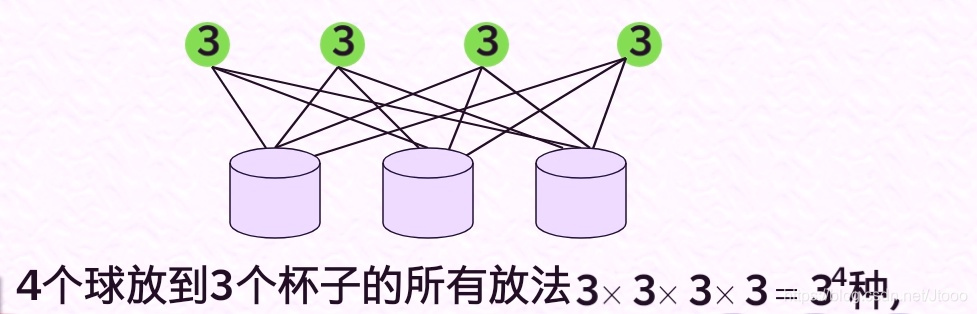
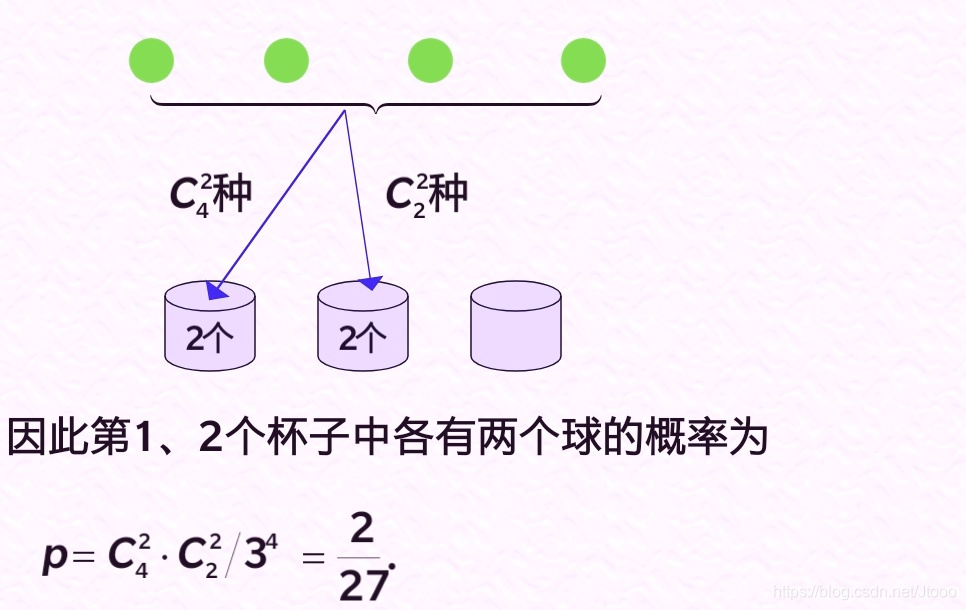
问题1 把 4 个球放到 3个杯子中去,求第1、2个
杯子中各有两个球的概率, 其中假设每个杯子可
放任意多个球.


(2) 每个杯子只能放一个球
问题2 把4个球放到10个杯子中去,每个杯子只能
放一个球, 求第1 至第4个杯子各放一个球的概率.

四、几何定义