DeepSpeech模型推导

百度 2014 年提出 Deep Speech 模型（语音识别领域的里程碑模型） ，它是端到端语音识别的早期代表性方案

Deep Speech 是首个大规模应用的端到端语音识别模型，与传统 HMM-ASR 方案相比，实现了 “从语音到文本” 的直接映射，大幅简化了流程。

怎么理解端到端

端到端是 “跨任务的通用概念”，AI 任务中 “输入→输出直接映射” 的模型都可以称为端到端

任务类型	端到端模型示例	非端到端的传统方案
图像分类	AlexNet、ResNet	人工提取 HOG 特征 + SVM 分类
语音识别	Deep Speech、Whisper	HMM+GMM（人工设计音素 + 多模块拼接）
机器翻译	Transformer（GPT）	分词→词向量→统计机器翻译（多模块串联）
目标检测	YOLO、Faster R-CNN	滑动窗口 + 人工特征提取 + 分类器

关键创新（与传统 HMM 方案的差异）

维度	Deep Speech 的设计	传统 HMM-ASR 的设计
声学模型	端到端训练的深度神经网络（DNN）	HMM+GMM/ANN 混合模型（分模块训练）
语音单元表示	完全取消音素级（Phone-level）表示，直接基于文本转录训练	依赖音素、音节等中间语音单元
输入特征	直接使用音频的频谱表示（无需 MFCC 等人工设计特征）	依赖人工
输出形式	字符级（Character-level）转录（直接输出文字字符）	通常为词级或音素级输出
训练与解码方式	使用 CTC（连接主义时序分类）损失函数和 CTC 解码	依赖 Viterbi 解码 + 语言模型后处理

Deep Speech 模型的架构模型

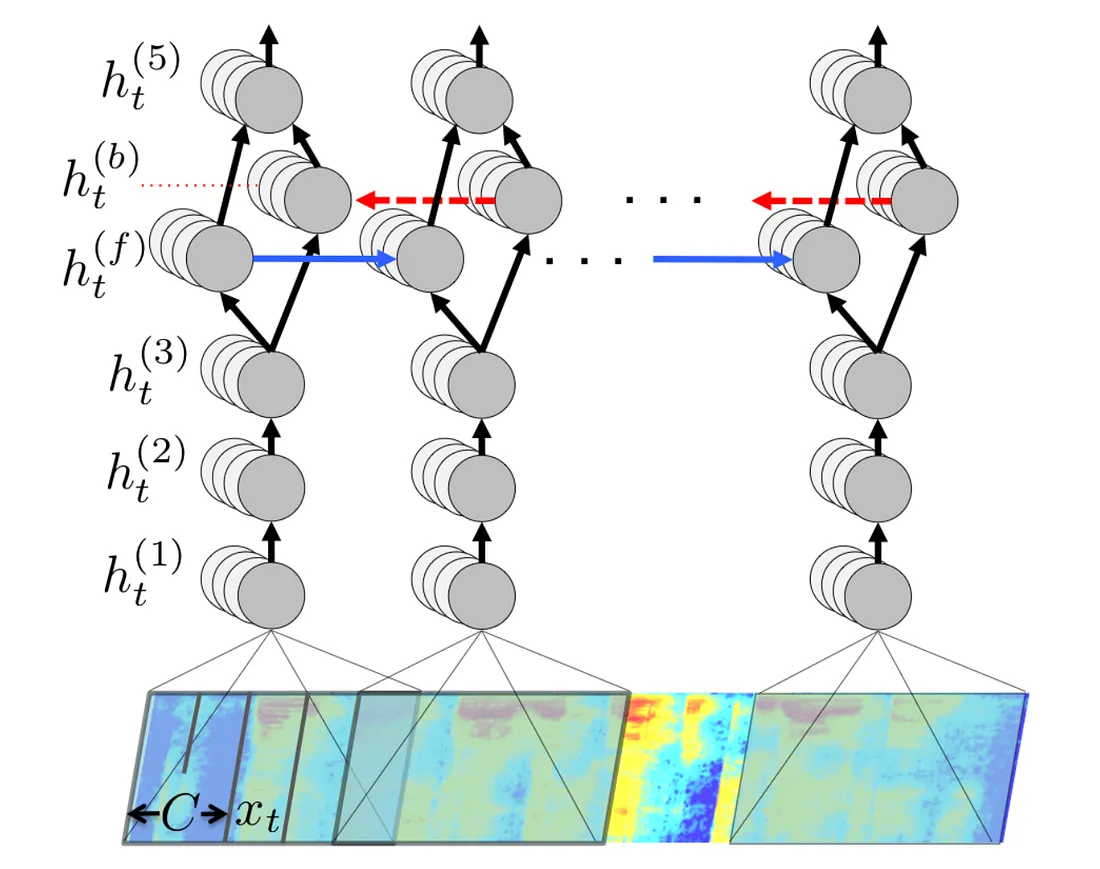
架构核心特点

Deep Speech 的网络结构非常简洁，仅包含 5 个隐藏层，关键设计如下：

• 隐藏层组成：仅 1 层是双向循环神经网络（RNN），且并非 LSTM（是基础 RNN 结构），其余为普通深度神经网络层；
• 输入处理：每个时间步的输入是 “滑动窗口内的多帧频谱”（即包含当前帧及前后相邻帧的频谱信息），以此捕捉语音的时序关联性。

以 “训练识别‘cat’” 为例

符号定义

• $\mathcal{X}=\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...\}$：训练数据集，每个样本是 “(输入频谱, 输出字符序列)” 对；
• $x^{(i)}$：第i个样本的输入频谱序列（比如 “cat” 是第 1 个样本，记为(x^{(1)})）；
• $T^{(i)}$：第i个样本的输入长度（帧数量）（比如 “cat” 样本的$T^{(1)}=5$，即 5 帧）；
• $x_t^{(i)}$：第i个样本的第t帧频谱（比如 “cat” 样本的第 2 帧是$x_2^{(1)}$）；
• $y^{(i)}$：第i个样本的输出字符序列（比如 “cat” 样本的$y^{(1)}=[\text{’c’},\text{’a’},\text{’t’}]$）；
• 注意：这里的$y^{(i)}$是最终字符序列，没有 “逐帧的$y_1^{(i)}\sim y_{T^{(i)}}^{(i)}$”（端到端模型不需要逐帧标签）。

“cat”（第 1 个样本，$i=1$）

• 输入：“cat” 的语音 → 切分为 5 帧频谱（记为 $x_1,x_2,x_3,x_4,x_5$，每帧是一个特征向量，比如长度为 100 的向量）；
• 输出：字符序列$y=[\text{’c’},\text{’a’},\text{’t’}]$（最终标签，无逐帧标签）；
• $x^{(1)}$：“cat” 的输入频谱序列（长度$T^{(1)}=5$，即 5 帧）；
• $x_t^{(1)}$：第 1 个样本的第t帧频谱（$t=1\sim 5$，对应$x_1^{(1)},x_2^{(1)},x_3^{(1)},x_4^{(1)},x_5^{(1)}$）；
• $y^{(1)}$：输出字符序列 “cat”（无逐帧(y_t^{(1)})）；
• 滑动窗口参数：$C=3$（窗口包含 “前 1 帧 + 当前帧 + 后 1 帧”）：每个$C\times x_t^{(1)}$是 “3 帧拼接的 300 维向量”（100×3）

步骤 1：生成第 1 个样本的$C\times x_t$

对第 1 个样本的每帧$x_t^{(1)}$（$t=1\sim 5$），生成滑动窗口输入：

• $t=1$：$C\times x_1^{(1)}=[\text{零向量},x_1^{(1)},x_2^{(1)}]$→ 300 维；
  • $x_1$无 “前 1 帧”，因此补零（或复制$x_1$）
• $t=2$：$C\times x_2^{(1)}=[x_1^{(1)},x_2^{(1)},x_3^{(1)}]$→ 300 维
• $t=3$：$C\times x_3^{(1)}=[x_2^{(1)},x_3^{(1)},x_4^{(1)}]$ → 300 维；
• $t=4$：$C\times x_4^{(1)}=[x_3^{(1)},x_4^{(1)},x_5^{(1)}]$ → 300 维；
• $t=5$：$C\times x_5^{(1)}=[x_4^{(1)},x_5^{(1)},零向量]$ → 300 维
  • $x_5$无 “后 1 帧”，因此补零

步骤 2：模型输入序列

模型的 “初始输入序列” 是：$[C\times x_1^{(1)},C\times x_2^{(1)},C\times x_3^{(1)},C\times x_4^{(1)},C\times x_5^{(1)}]$（共 5 个时刻，每个时刻 300 维）

步骤 3：前三层全连接层的处理（特征提炼）

全连接层 1：

• 输入：每个时刻的 300 维向量（比如$t=2$的 300 维向量）；
• 处理：通过权重矩阵（300×128）和偏置，计算后用 ReLU 激活；
• 输出：每个时刻的 128 维特征向量（记为$h_1^{(1)}(t)$，$t=1\sim 5$）

$h_1^{(i)}(t)=\text{ReLU}(W_1\times (C\times x_t^{(i)})+b_1)$
其中$W_1$是 300×128 权重，$C$是滑动窗口大小，$b_1$是 128 维偏置

例：$t=2$的输出 $h_1^{(1)}(2)=\text{ReLU}(W_1\times (C\times x_2^{(1)})+b_1)$。

全连接层 2：

• 输入：全连接层 1 输出的 128 维向量$(h_1^{(1)}(t)$）；
• 处理：权重矩阵（128×128）+ ReLU 激活；
• 输出：每个时刻的 128 维特征向量（$h_2^{(1)}(t)$）。

$h_2^{(i)}(t)=\text{ReLU}(W_2\times (h_1^{(i)}(t)+b_2)$

其中$W_2$是 [128, 128] 的权重矩阵，$b_2$是 128 维偏置。

全连接层 3：

• 输入：全连接层 2 输出的 128 维向量($h_2^{(1)}(t)$）；
• 处理：权重矩阵（128×128）+ ReLU 激活；
• 输出：每个时刻的 128 维特征向量（$h_3^{(1)}(t)$）。
  $h_3^{(i)}(t)=\text{ReLU}(W_3\times (h_2^{(i)}(t)+b_3)$
  其中$W_3$是 [128, 128] 的权重矩阵，$b_3$是 128 维偏置。

经过前三层全连接层后，模型的输入序列被转换为：$[h_3^{(1)}(1),h_3^{(1)}(2),h_3^{(1)}(3),h_3^{(1)}(4),h_3^{(1)}(5)]$（共 5 个时刻，每个时刻 128 维）。

步骤 4：双向 RNN 层（捕捉时序关联）

双向 RNN 的作用：在前三层全连接层提炼的 “帧级抽象特征” 基础上，同时捕捉 “过去→现在” 和 “未来→现在” 的时序关联—— 比如识别 “a”（第 3 帧）时，既要知道前面是 “c”（第 1-2 帧），也要知道后面是 “t”（第 4-5 帧），才能准确判断这个 “a” 是 “cat” 中的 “a”，而不是 “bat” 或 “car” 中的 “a”。

双向 RNN 由两个独立的单向 RNN组成（前向 RNN + 后向 RNN），共享同一输入序列，但信息流动方向相反：

组件	信息流动方向	核心作用	对应 “cat” 的处理逻辑
前向 RNN（Forward RNN）	从左到右（t=1→t=5）	捕捉 “过去→现在” 的依赖（如 c→a 的衔接）	先看 $h_3^{(1)}(1)$（c 的特征）→ $h_3^{(1)}(2)$（c 的特征）→ $h_3^{(1)}(3)$（a 的特征）→ …，记住前面的发音序列
后向 RNN（Backward RNN）	从右到左（t=5→t=1）	捕捉 “未来→现在” 的依赖（如 a→t 的衔接）	先看 $h_3^{(1)}(5)$（t 的特征）→ $h_3^{(1)}(4)$（t 的特征）→ $h_3^{(1)}(3)$（a 的特征）→ …，记住后面的发音序列

两个 RNN 的参数（权重、偏置）完全独立，仅输入序列相同。

RNN 层的输入

全连接层 3 输出的特征序列为：
$[h_3^{(1)}(1),h_3^{(1)}(2),h_3^{(1)}(3),h_3^{(1)}(4),h_3^{(1)}(5)]$
（5 个时刻，每个时刻 128 维特征向量，对应 “cat” 的 5 帧）

信息流动过程

用$h_{forward}(t)$表示前向 RNN 在 t 时刻的输出，$h_{backward}(t)$表示后向 RNN 在 t 时刻的输出，均为 128 维

1. 前向 RNN 的逐时刻计算（t=1→t=5）

前向 RNN 的输出依赖「当前时刻输入特征 + 前一时刻的前向输出」，公式为：
$h_{\text{forward}}(t)=\text{ReLU}\left(W_{\text{xf}}\cdot h_3^{(1)}(t)+W_{\text{hf}}\cdot h_{\text{forward}}(t-1)+b_f\right)$

• $W_{\text{xf}}$：输入特征到前向 RNN 的权重矩阵（128×128）；
• $W_{\text{hf}}$：前一时刻输出到当前时刻的权重矩阵（128×128）；
• $b_f$：前向 RNN 的偏置（128 维）；
• 初始状态 $h_{\text{forward}}(0)$：全零向量（无过去信息时的默认值）。

具体到 “cat”：

• t=1：输入 $h_3^{(1)}(1)$（c 的特征）→ 输出 $h_{\text{forward}}(1)=\text{ReLU}(W_{\text{xf}}\cdot h_3^{(1)}(1)+W_{\text{hf}}\cdot 0+b_f)$ → 仅包含 c 的特征信息；
• t=2：输入 $h_3^{(1)}(2)$（c 的特征）→ 输出 $h_{\text{forward}}(2)=\text{ReLU}(W_{\text{xf}}\cdot h_3^{(1)}(2)+W_{\text{hf}}\cdot h_{\text{forward}}(1)+b_f)$ → 包含 “c→c” 的连续信息；
• t=3：输入 $h_3^{(1)}(3)$（a 的特征）→ 输出$h_{\text{forward}}(3)=\text{ReLU}(W_{\text{xf}}\cdot h_3^{(1)}(3)+W_{\text{hf}}\cdot h_{\text{forward}}(2)+b_f)$ → 包含 “c→c→a” 的衔接信息；
• t=4：输入 $h_3^{(1)}(4)$（t 的特征）→ 输出 $h_{\text{forward}}(4)$ → 包含 “c→c→a→t” 的衔接信息；
• t=5：输入 $h_3^{(1)}(5)$（t 的特征）→ 输出 $h_{\text{forward}}(5)$ → 包含完整的 “c→c→a→t→t” 前向序列信息。

2. 后向 RNN 的逐时刻计算（t=5→t=1）

后向 RNN 的输出依赖「当前时刻输入特征 + 后一时刻的后向输出」，公式为：
$h_{\text{backward}}(t)=\text{ReLU}\left(W_{\text{xb}}\cdot h_3^{(1)}(t)+W_{\text{hb}}\cdot h_{\text{backward}}(t+1)+b_b\right)$

• $W_{\text{xb}}$：输入特征到后向 RNN 的权重矩阵（128×128）；
• $W_{\text{hb}}$：后一时刻输出到当前时刻的权重矩阵（128×128）；
• $b_b$：后向 RNN 的偏置（128 维）；
• 初始状态 $h_{\text{backward}}(6)$：全零向量（无未来信息时的默认值）。

具体到 “cat”：

• t=5：输入 $h_3^{(1)}(5)$（t 的特征）→ 输出 $h_{\text{backward}}(5)=\text{ReLU}(W_{\text{xb}}\cdot h_3^{(1)}(5)+W_{\text{hb}}\cdot 0+b_b)$ → 仅包含 t 的特征信息；

• t=4：输入 $h_3^{(1)}(4)$（t 的特征）→ 输出 $h_{\text{backward}}(4)=\text{ReLU}(W_{\text{xb}}\cdot h_3^{(1)}(4)+W_{\text{hb}}\cdot h_{\text{backward}}(5)+b_b)$ → 包含 “t→t” 的连续信息；

• t=3：输入 $h_3^{(1)}(3)$（a 的特征）→ 输出 $h_{\text{backward}}(3)=\text{ReLU}(W_{\text{xb}}\cdot h_3^{(1)}(3)+W_{\text{hb}}\cdot h_{\text{backward}}(4)+b_b)$ → 包含 “a→t→t” 的衔接信息；

• t=2：输入 $h_3^{(1)}(2)$（c 的特征）→ 输出 $h_{\text{backward}}(2)$ → 包含 “c→a→t→t” 的衔接信息；

• t=1：输入 $h_3^{(1)}(1)$（c 的特征）→ 输出 $h_{\text{backward}}(1)$ → 包含完整的 “c→c→a→t→t” 后向序列信息。

3. 双向 RNN 的最终输出（拼接前向 + 后向）

每个时刻 t 的双向 RNN 输出，是「前向输出 + 后向输出」的向量拼接，维度从 128 维→256 维：$h_{\text{biRNN}}(t)=\text{concat}\left(h_{\text{forward}}(t),h_{\text{backward}}(t)\right)$

对应 “cat” 的关键时刻 t=3（a 的特征帧）：

• $h_{\text{biRNN}}(3)=\text{concat}(h_{\text{forward}}(3),h_{\text{backward}}(3))$ → 256 维向量；
• 其中：$h_{\text{forward}}(3)$ 包含 “c→c→a” 的前向信息，$h_{\text{backward}}(3)$ 包含 “a→t→t” 的后向信息；
• 最终，t=3 的输出同时包含 “a 前面是什么” 和 “a 后面是什么”，让模型明确这是 “cat” 中的 “a”

双向 RNN 的核心作用（为什么必须用双向？）

1. 解决语音的 “上下文依赖” 问题：语音是连续的，单个帧的特征没有明确含义，必须结合前后发音才能判断。比如单独看 h3 (3)（a 的特征），无法确定是 “cat”“bat” 还是 “car”，但结合前向的 “c” 和后向的 “t”，就能唯一确定是 “cat” 中的 “a”。
2. 提升字符预测的准确性：前文输出层的字符概率分布（如 t=3 预测 “a” 的概率 0.95），依赖双向 RNN 的 256 维特征 —— 因为这个特征包含了完整的上下文，模型能更自信地判断当前帧对应的字符。
3. 替代传统 HMM 的时序建模：传统 HMM 需要单独建模音素的转移概率（如 c→a 的转移概率），而双向 RNN 通过学习特征序列的时序关联，直接在模型内部实现了 “时序建模”，这也是端到端模型能跳过 HMM 的关键原因之一。

步骤 5：输出层（全连接层 4）→ 字符概率分布

输出层的作用：把 RNN 的 256 维特征向量，映射为 “所有字符的概率分布”：

• 假设字符集大小为 30（26 字母 + 空格 + 撇号 + 空字符）；

• 输入：双向RNN 输出的 256 维向量（$h_{biRNN}^{(1)}(t)$）；

• 处理：权重矩阵（256×30）+ Softmax 激活（把输出转换为概率，总和为 1）；

• 输出：每个时刻的 30 维字符概率分布 $p(c_t^{(1)}|x^{(1)})$。

  • $c_t^{(1)}$是第t时刻预测的字符
  • 上标$(1)$：代表第 1 个样本（即 “cat” 样本）
  • $x^{(1)}$：第 1 个样本的输入频谱序列；
  • 整体含义：“在第 1 个样本的输入$x^{(1)}$下，第t时刻预测为字符$c_t^{(1)}$的概率”

全连接层 4 的映射分为线性变换和非线性激活两步：

步骤 1：线性变换（计算 Softmax 的输入z(t)）

线性变换的公式为：

$z(t)=W_o\cdot h_{biRNN}(t)+b_o$

符号解释：

• z(t)：第t时刻的 30 维字符得分向量（Softmax 的输入向量，未归一化的 “对数概率” 或 “得分”）；
• $W_o$：权重矩阵（30×256），每一行对应一个字符的权重；
• $h_{biRNN}(t)$：第t时刻的RNN 输出（256×1 列向量）；
• $b_o$：偏置向量（30×1 列向量），每一行对应一个字符的偏置；

逐元素展开（第k个字符的得分）：

$z_k(t)={\sum }_{i=1}^{256}{W}_{o,k,i}\cdot h_{biRNN,i}(t)+b_{o,k}$

$W_{o,k,i}$是权重矩阵第k行第i列的元素，$h_{biRNN,i}(t)$是 RNN 输出第i个元素，$b_{o,k}$是偏置第k个元素）

步骤 2：Softmax 激活（转换为概率分布$y_{hat}(t)$）

Softmax 激活的作用是将 30 维字符得分转换为 30 维概率分布（总和为 1），公式为：

$y_{\text{hat,k}}(t)=\frac{\exp (z_{\text{k}}(t))}{{\sum }_{j=1}^{30}\exp (z_{\text{j}}(t))}$

符号解释：

• $y_{\text{hat},k}(t)$：第t时刻第k个字符的概率（30 维分布的第k个元素）；
• exp()：指数函数（将得分转换为正数）；
• 分母：所有字符得分的指数和（归一化因子，保证概率和为 1）。

对 “cat” 的 5 个时刻30 维概率分布（重点关注’c’、‘a’、‘t’、'ε’的概率）

时刻t	字符 0（‘a’）	字符 2（‘c’）	字符 19（‘t’）	字符 28（‘ε’）	其他字符（26 个）	30 维概率和
1	0.01	0.92	0.01	0.05	0.01（26 个字符均分，每个≈0.0004）	1.00
2	0.02	0.88	0.01	0.07	0.02（每个≈0.0008）	1.00
3	0.95	0.01	0.01	0.02	0.01（每个≈0.0004）	1.00
4	0.01	0.01	0.90	0.06	0.02（每个≈0.0008）	1.00
5	0.01	0.01	0.85	0.10	0.03（每个≈0.0012）	1.00

t=3 时刻的 30 维概率分布向量y_hat(3)可明确写为：$y_{hat}(3)=[0.95,0.0004,0.01,0.0004,...,0.01,0.0004,...,0.02,0.0004]$

对应：

[索引0（'a'）, 索引1（其他字符）,  索引2（'c'）, 索引3（其他字符）,  索引4-18（其他字符，各个 ≈0.0004）, 索引19（'t'）, 索引20（其他字符）,  索引21-27（其他字符，各≈0.0004）,  索引28（'ε'）, 索引29（其他字符）]

（所有元素求和 = 1.00）

步骤 6：CTC 损失计算

CTC 损失的核心目标

CTC（连接主义时序分类）损失的作用是：在 “输入帧数量≠输出字符数量” 且 “无逐帧标签” 的情况下，计算 “模型预测的帧级字符序列” 与 “真实字符序列” 的匹配误差，让模型学会 “从多帧预测中提炼出正确的字符序列”。

以 “cat” 样本为例的 CTC 损失计算步骤

已知条件：

• 模型输入：“cat” 的 5 帧特征序列（对应 5 个时刻的预测）；
• 模型输出：5 个时刻的字符概率分布（预测序列：c→c→a→t→t）；
• 真实标签：字符序列$y=[\text{’c’},\text{’a’},\text{’t’}]$（长度 3）。

步骤 1：构造 “扩展标签序列”（处理长度不匹配）

CTC 会在真实标签中插入空字符（记为ε），构造 “扩展标签序列”，使其长度≥输入帧数量的一半（保证能对齐）。

• 真实标签：[c, a, t] （U=3）
• 扩展标签序列：[ε, c, ε, a, ε, t, ε]（长度为2U+1=7≥5/2）

扩展标签的生成规则

扩展标签（记为y’）是对真实标签y 的改造，目的是为了让 “长度为T的帧序列” 能通过 “插入空字符、重复字符” 与 “长度为U的真实字符序列” 对齐。生成规则只有 2 条：

• 规则 1：在真实标签的每个字符之间插入 “空字符ε”；
• 规则 2：在真实标签的开头和结尾也插入 “空字符ε”。

步骤 2：寻找 “有效对齐路径”（预测序列→标签序列的合法映射）

有效对齐路径是指：预测序列（5 帧）通过 “合并重复字符、跳过空字符” 后，能得到真实标签[c,a,t]的所有可能字符序列。

以 “cat” 的预测序列c→c→a→t→t为例，有效对齐路径是：

• 路径 1：c（t1）→ c（t2）→ a（t3）→ t（t4）→ t（t5）
• 路径 2：c（t1）→ ε（t2）→ a（t3）→ t（t4）→ t（t5）（若 t2 预测为空字符）
• …（所有满足 “合并后为 c-a-t” 的序列）

前向 - 后向算法

前向 - 后向算法是动态规划在 CTC 时序对齐问题中的具体应用 —— 通过 “状态转移” 和 “递推计算”，避免枚举所有有效路径（指数级复杂度），以 O(T×U²) 复杂度高效求出所有有效路径的概率之和（T 是输入帧数量，U 是真实标签长度）。

在 CTC 中：

• 「大问题」：计算所有有效路径的概率之和（比如 5 帧对应 3 个字符，有效路径可能有上百条，枚举会爆炸）；
• 「小问题」：计算 “前 t 帧匹配到扩展标签第 s 位” 的概率（即前向变量${\alpha }_t(s)$）；
• 「中间结果」：存储每个t和s对应的${\alpha }_t(s)$，后续计算直接复用，无需重复计算历史路径。

结合 “cat” 的扩展标签 y’ = [ε, c, ε, a, ε, t, ε]（长度 7，记为s=1~7）和 5 帧（t=1~5），解释递推逻辑：

1. 定义 “状态”：前向变量${\alpha }_t(s)$:

状态定义是动态规划的灵魂，CTC 中定义：

${\alpha }_t(s)=前t帧匹配到扩展标签第s位的所有有效路径的概率之和$

• 比如 ${\alpha }_3(4)$：前 3 帧匹配到扩展标签第 4 位（字符a）的所有有效路径的概率和；
• 状态的维度是 T×(2U+1)（T=5，2U+1=7），共 35 个状态（远少于枚举的路径数）。

5 个时刻的 30 维概率分布（核心字符）：

t	$y_{\text{hat},t}(\epsilon )$	$y_{\text{hat},t}(c)$	$y_{\text{hat},t}(a)$	$y_{\text{hat},t}(t)$
1	0.05	0.92	0.01	0.01
2	0.07	0.88	0.02	0.01
3	0.02	0.01	0.95	0.01
4	0.06	0.01	0.01	0.90
5	0.10	0.01	0.01	0.85

$y_{\text{hat},t}(\epsilon )$是30 维向量$y_{\text{hat}}(t)$中第 28 位的元素值（t=3 时刻为 0.02）

2. 定义 “状态转移”：从t-1帧到t帧的概率传递

对于第t帧的状态s（扩展标签第s位字符y'[s]），其概率${\alpha }_t(s)$只能来自第t-1帧的有限几个相邻状态（避免枚举所有路径），转移规则由 CTC 合并逻辑推导而来：

• 转移来源 1：前一帧也在s位（对应 “重复字符”，比如t-1帧和t帧都匹配c）；
• 转移来源 2：前一帧在s-1位（对应 “正常推进”，比如t-1帧匹配ε，t帧匹配c）；
• 转移来源 3：前一帧在s-2位（对应 “跳过空字符”，比如t-1帧匹配c，t帧直接匹配a，跳过中间的ε）。

转移公式：

${\alpha }_t(s)=\{\begin{array}{ll}\text{t=1（}初始状态\text{）：}& {\alpha }_1(1)=y_{\text{hat},1}(y^{\prime }[1]),{\alpha }_1(2)=y_{\text{hat},1}(y^{\prime }[2]),\text{其余}=0\\ t\ge 2,s=1\text{：}& {\alpha }_{t-1}(1)\times y_{\text{hat},t}(y^{\prime }[1])\\ t\ge 2,s\ge 2\text{：}& \left({\alpha }_{t-1}(s)+{\alpha }_{t-1}(s-1)+\text{（若}{y}^{\prime }[s]\ne \epsilon \text{且}{y}^{\prime }[s]\ne y^{\prime }[s-2]\text{，则加}{\alpha }_{t-1}(s-2)\text{）}\right)\times y_{\text{hat},t}(y^{\prime }[s])\end{array}$

（约束：空字符(ε)不能跳过自身，连续相同字符只能从相邻状态转移）

最后乘以 $y_{hat,t}(y^{\prime }[s])$：第t帧预测扩展标签第s位字符的概率（从 30 维分布中取值）。

3. 递推计算

t=1帧的初始状态（只有s=1[ε]和s=2[c] 有概率，其余为 0）：

• $s=1$：${\alpha }_1(1)=y_{\text{hat},1}(\epsilon )=0.05$
• $s=2$：${\alpha }_1(2)=y_{\text{hat},1}(c)=0.92$
• $s=3\sim 7$：${\alpha }_1(s)=0$（第 1 帧无法匹配后面的标签）

t=2

• $s=1$（字符$\epsilon$）：
  只能从$t=1$的$s=1$转移（$\epsilon$不能跳过自身）
  ${\alpha }_2(1)={\alpha }_1(1)\times y_{\text{hat},2}(\epsilon )=0.05\times 0.07=0.0035$

• $s=2$（字符c）：$c\ne \epsilon$且$c\ne y^{\prime }[0]$（$s-2=0$不存在），故只加${\alpha }_1(2)+{\alpha }_1(1)$：
  ${\alpha }_2(2)=\left({\alpha }_1(2)+{\alpha }_1(1)\right)\times y_{\text{hat},2}(c)=(0.92+0.05)\times 0.88=0.8536$

• $s=3$（字符$\epsilon$）：只能从$t=1$的$s=2$转移（$\epsilon$不能跳过自身）：${\alpha }_2(3)={\alpha }_1(2)\times y_{\text{hat},2}(\epsilon )=0.92\times 0.07=0.0644$

• $s=4\sim 7$：${\alpha }_2(s)=0$（第 2 帧无法匹配后面的标签）

t=3

• s=1（字符$\epsilon$）：
  从t=2的s=1转移：
  ${\alpha }_3(1)={\alpha }_2(1)\times y_{\text{hat},3}(\epsilon )=0.0035\times 0.02=0.00007$

• s=2（字符c）：
  ${\alpha }_3(2)=\left({\alpha }_2(2)+{\alpha }_2(1)\right)\times y_{\text{hat},3}(c)=(0.8536+0.0035)\times 0.01\approx 0.00857$

• s=3（字符(ε)）：
  ${\alpha }_3(3)=\left({\alpha }_2(3)+{\alpha }_2(2)\right)\times y_{\text{hat},3}(\epsilon )=(0.0644+0.8536)\times 0.02=0.01836$

• s=4（字符a）：
  ${\alpha }_3(4)=\left({\alpha }_2(4)+{\alpha }_2(3)+{\alpha }_2(2)\right)\times y_{\text{hat},3}(a)=(0+0.0644+0.8536)\times 0.95=0.8671$

• $s=5\sim 7$：${\alpha }_3(s)=0$

t=4

• s=1（字符$\epsilon$）：${\alpha }_4(1)={\alpha }_3(1)\times y_{\text{hat},4}(\epsilon )=0.00007\times 0.06\approx 0.000004$
• s=2（字符$c$）：${\alpha }_4(2)=\left({\alpha }_3(2)+{\alpha }_3(1)\right)\times y_{\text{hat},4}(c)=(0.00857+0.00007)\times 0.01\approx 0.000086$
• s=3（字符$\epsilon$）：${\alpha }_4(3)=\left({\alpha }_3(3)+{\alpha }_3(2)\right)\times y_{\text{hat},4}(\epsilon )=(0.01836+0.00857)\times 0.06\approx 0.001616$
• s=4（字符$a$）：${\alpha }_4(4)=\left({\alpha }_3(4)+{\alpha }_3(3)+{\alpha }_3(2)\right)\times y_{\text{hat},4}(a)=(0.8671+0.01836+0.00857)\times 0.01\approx 0.00894$
• s=5（字符$\epsilon$)）：$\alpha_4(5) = \left( \alpha_3(5) + \alpha_3(4) \right) \times y_{\text{hat},4}(ε) = (0+0.8671) \times 0.06 = 0.052026
• s=6：${\alpha }_4(6)=\left({\alpha }_3(6)+{\alpha }_3(5)+{\alpha }_3(4)\right)\times y_{\text{hat},4}(t)=(0+0+0.8671)\times 0.90=0.78039$
• s=7：${\alpha }_4(7)=0$

t=5

• s=1（字符$\epsilon$）：${\alpha }_5(1)={\alpha }_4(1)\times y_{\text{hat},5}(\epsilon )=0.000004\times 0.10\approx 0.0000004$
• s=2
• s=3
• s=4
• s=5
• s=7

通过这种方式，每帧只需要计算 7 个状态（扩展标签长度），每个状态最多依赖 3 个前序状态，高效递推。

步骤 3：计算总概率P(y|x)

总概率是最后一帧匹配扩展标签最后两位（$t$或$\epsilon$）的概率之和：

• 对任意真实标签y（长度U），扩展标签的长度是$2U+1$，总概率的计算规则是：$P(y|x)={\alpha }_T(2U)+{\alpha }_T(2U+1)$
  • $T$：输入帧的数量（比如 “cat” 的(T=5)）；
  • $2U$：扩展标签的倒数第二位（对应真实标签的最后一个字符）；
  • $2U+1$：扩展标签的最后一位（对应结尾的空字符$\epsilon$）。

总概率验证$P(y|x)={\alpha }_5(6)+{\alpha }_5(7)\approx 0.7167+0.07804\approx 0.7947$
通过完整递推可以看到：前向变量${\alpha }_t(s)$通过 “状态转移 + 约束”，自动覆盖了所有有效路径的概率，无需枚举，且只保留对总概率有贡献的状态。

步骤 4：计算 CTC 损失

CTC 损失是 “总概率的负对数”（负对数能将 “概率最大化” 转化为 “损失最小化”，符合梯度下降的优化逻辑）：

$CT{C}_{\text{Loss}}=-\log (P(y|x))=-\log (0.7947)\approx 0.23$

这个损失值（≈0.230）表示：

• 模型当前的匹配度：模型的 5 帧预测序列与真实标签cat的匹配置信度约为 79.47%（总概率），损失越小说明匹配度越高；
• 模型需要优化的方向：损失 > 0，说明模型还有优化空间（比如让 t=3 帧a的概率更集中、t=4 帧t的概率更高）。

步骤7：模型更新过程（反向传播）

得到 CTC 损失后，通过反向传播算法调整模型所有参数（前三层全连接层、双向 RNN、输出层的权重和偏置）

CTC 损失的梯度需要反向传播到输出层→双向 RNN→前三层全连接层，核心是计算 “损失对输出层概率y_hat_t©的梯度”，再逐层传递。

步骤 1：计算损失对输出层的梯度输出层的输出是 “每个时刻的字符概率分布”，损失对输出层第t时刻字符c的梯度为：
$\frac{\partial \text{Loss}}{\partial p(c|t)}=-\frac{1}{P(y|x)}\times \text{该字符在有效路径中的总贡献概率}$

步骤 2：梯度从输出层向 RNN 层反向传播输出层的梯度会传递到双向 RNN 层，计算损失对 RNN 输出的梯度，再进一步分解为 “前向 RNN” 和 “后向 RNN” 的梯度，调整 RNN 的权重$W_{\text{xf}}、W_{\text{hf}}、W_{\text{xb}}、W_{\text{hb}}$等参数。
步骤 3：梯度向全连接层反向传播RNN 层的梯度继续传递到前三层全连接层，计算损失对全连接层权重（$W_1、W_2、W_3$）和偏置（$b_1、b_2、b_3$）的梯度。
步骤 4：梯度下降更新参数用梯度下降法（如 SGD、Adam）调整所有参数：${\theta }_{\text{new}}={\theta }_{\text{old}}-\alpha \times \frac{\partial \text{Loss}}{\partial {\theta }_{\text{old}}}$
其中$\alpha$是学习率（控制参数更新的步长）。