简略信息熵

1.信息量

发生概率越小，信息量越大；发生概率越大，信息量越小

2.熵

熵(entropy):上面的Ⅰ(x)是指在某个概率分布之下,某个概率值对应的信息量的公式.那么我们要知道这整个概率分布对应的信息量的平均值.这个平均值就叫做随机变量x的熵 

基于图来看

1.当p=0或者p=1的时候,随机变量可以认为是没有不确定性.
2.当p=0.5的时候,H(p)=1,随机变量的不确定性最大.

2. 相对熵

相对熵又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度（即KL散度）等。
设p(x)和q(x)是取值的两个概率概率分布，则p对q的相对熵为: 

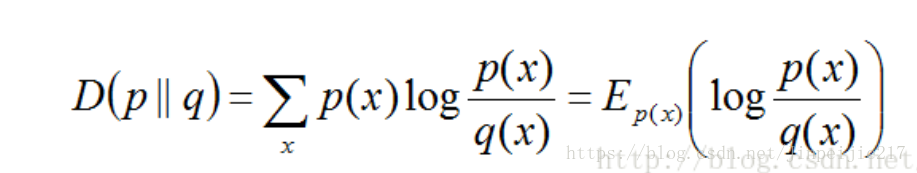
3. 互信息

互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不确定性。
两个随机变量X,Y的互信息，定义为X,Y的联合分布和独立分布乘积的相对熵。 

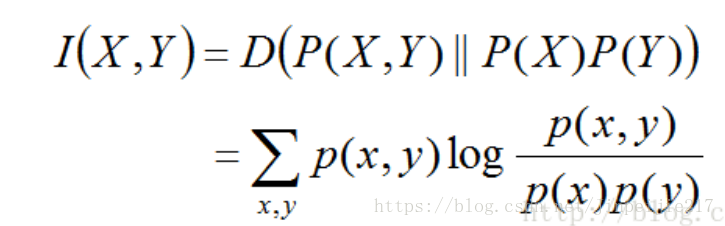
从这个公式可以知道，X的熵减去X和Y的互信息之后，可以得到在Y给定的情况下X的熵。