白话理解熵、信息量、信息熵、决策树思想

---

一、熵是什么？

如果你说高中的理科生，或者学过化学的同学，很简单，熵描述的就是一个混乱程度的概念。
什么是混乱？

这些都是很抽象的概念，白话理解就是，我随机地做一件事，被你猜到的难度有多大。
来一个有趣的例子：
小时候你们家有没有丢过钥匙？

假设你们家现在要去一起出门去玩。为了谨防小偷，那必须先锁门。于是你们要先找钥匙来开门。此时，你会发现你们家的钥匙历史期间落在很过个地方。它们分别是：

• A.爸妈卧室的枕头底，
• B.电视机的下面柜子第二格，
• C.客厅的水果盆后面，
• D.爸妈房间的门上挂着，
• E.沙发椅的角落里，
• F.在你的手里就拿着钥匙去找钥匙。（大无语事件）

现在只有一次机会去以上的任意一个地方找钥匙：
那么：
“你一次找到这个钥匙的难度有多大” 等价于 这个钥匙的历史落在地方的混乱程度，等价于钥匙落在地方这个事件的信息熵的大小。

1. 试想一下，这个问题中，什么情况下是最难一次找到这个钥匙的？
   那就是过往中你们家的钥匙几乎落在上述的 A、B、C、D、E、F 的6个地方的次数基本是完全一样的。（是不是感慨一句，你们家到底有多乱）这时候钥匙摆放就是最乱的，相对地理解就是你一次找到钥匙的事件可能性是最低的，也就是你很难一次就找到你的钥匙。
   以上上述的是字面的理解日常生活的难度，混乱程度等概念。
   那么如果要做一个科学研究的话，那就是一个有公式，有指标的概念。
   这个熵，就是熵/香农熵。

二、信息量与信息熵

信息量是什么？我们日常生活中，其实经常用到。
2. 周杰伦饿了会吃饭的哟。（废话，人饿了都会去吃饭，基本没什么信息量）
3. 小明放学回家被狗咬了。（有点信息量，村里的狗太多了，被狗咬也不为怪）
4. 小明今天把狗咬了。（信息量很大，小明竟把狗给咬了，一般人不会这样做）
5. 抛一枚硬币，是正面。
6. …
以上就是日常用语。归根到底就是那句话“狗咬人算不上什么新闻，人咬狗才是新闻。”
这其实就是信息量的概念。
一个事件的出现概率本来是很低的，但是它出现了，则说明这个事件的信息量很大。新闻的价值很大！
来看三个要点：

1. 概率越低则信息量越大，我们想想这应该是一个单调递减的函数。
2. 并且这个事件概率的范围是0-1。
3. 当我们知道这个事件是百分百会出现的时候，它就等于没有信息量。（在在日期2022年7月11日）太阳从东方升起。也就是必然过一个定点（1，0）

符合以上的条件有什么呢？

底数a取值范围为（0，1）的对数函数！

几分之几好麻烦，我们通常把底数换做一个大于1的数，怎么办？底数必然是一个0-1 的负数，怎么办？换底公式！


以上描述了这个信息量：出现的概率越大则信息量越小
（关于底数的取值：底数为2 ，单位为bit /比特，底数为自然对数e,则单位是nat/奈特）
信息量=信息熵？
错！信息熵是信息量的加权平均。就是整个事件出现的情况的期望。
譬如：抛硬币有2种情况
正面、反面朝上的信息量为：

那么整个抛硬币的事件中信息熵是1+1=2？
错！信息熵是一种加权的平均，应为1，与下图计算判断题一样，信息熵描述的是整个事件的本身的混乱程度（来把握这个事件的难易程度），信息量是描述一个事件的一种情况出现难易程度。

信息熵的公式为：

你会发现去考试的时候出选择题的（ABC）三个选项的比判断题（对错）的难，但又比选择题（ABCD）四个选项的简单。下面假设上述的所有选项都是等概率出现。那么来算一下这几个事件的信息熵。

• 选择题ABC：
  
• 选择题ABCD：
  
• 判断题：
  
  可见用信息熵来描述做选择题ABCD难度>选择题ABC>判断题

计算信息熵为什么是对数函数？

来回忆下上面说的三个计算信息量的条件：

1. 概率越低则信息量越大，我们想想这应该是一个单调递减的函数。
2. 并且这个事件概率的范围是0-1。
3. 当我们知道这个事件是百分百会出现的时候，它就等于没有信息量。（2022年7月11日）太阳从东方升起。也就是 必然过一个定点（1，0）
   符合信息量的就算还有很多函数：
   

如:

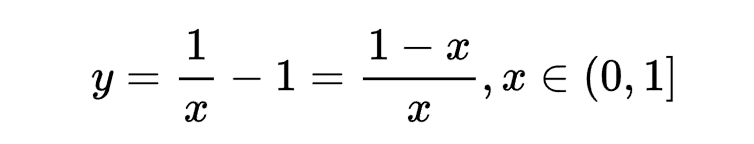
具有描述信息量的性质，但是不符合信息熵种描述的信息量之间的关系！

这是描述信息量的条件。因为除了描述信息量之外，我们还要定义一种事件信息量与信息量之间的关系。

譬如说，做对一道等概率出现的选择题（ABCD）的难度与做对等概率出现的两道判断题（对错）是等价的。

证明：
将两道判断题稍微做个类似编码的东西即可：
两道选择题的答案转化为一道四个选项的判断题：
A，对对；B，对错，C，错对，D对对
证毕

在对数函数可以体现出这种信息量之间的关系，因为对数的定义：

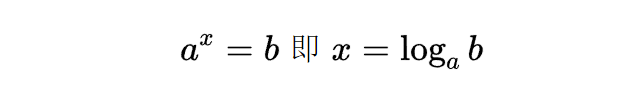
在上面的计算信息熵例子里也知道了，选择题ABCD的信息熵为2，判断题的为1，他们是一种两倍的关系。在这里可以体现出来了。
还有一点，有一个无穷接近但是不等于0的概率(x,p)约束，对于线性函数或者简单的幂函数是不可以描述。概率可能是一个无穷小的正数，此时信息量为无穷大。例如：夏天广州下雪。
再看看对数的泰勒展开：

是无穷多项高阶幂函数叠加的函数。

三、决策树思想

决策树是机器学习的一种重要的监督学习方法。它的思想和信息有什么关系？本文以ID3 决策树为例。讲述决策树的思想。

还是回到找钥匙的例子：

 - A.爸妈卧室的枕头底， 
 - B.电视机的下面柜子第二格，
 - C.客厅的水果盆后面， 
 - D.爸妈房间的门上挂着， 
 - E.沙发椅的角落里，

• F.在你的手里就拿着钥匙去找钥匙。（大无语事件）
  假如现在有一批数据，记录的是过往之中你们家找钥匙的情况。每次找到钥匙你都总结了下原因。分别是
• “刚刚有没有搞卫生”，
• “今天是不是周末”，
• “刚刚有没有看电视”，
  假设搞清楚这几个问题就能搞明白钥匙在哪。
  

决策树的思想

就是：
通过按照一定的先后顺序地询问你问题特征，来预测/判断问题标签。
在这里就是通过一定的顺序来询问，然后得出判断的结果。

如何确定特征属性（询问问题的顺序）？是决策树的关键。
现在从信息熵来理解觉得树。
当你要出去找钥匙的那一刻开始，你头脑空白，特征属性都不知道是怎么样的，你只知道以往中，在ABCDE五个位置的次数，那么很简单可以用信息量的期望----信息熵来描述这个钥匙摆放的混乱程度！这就是最初的信息熵。
但是你想想当你知道一个特征属性的任意一个问题的钥匙摆放后，是不是对这个钥匙摆放更加清楚了，也就是钥匙摆放的混乱程度降低了。
比如说“你知道今天是周末，爸妈拿钥匙的概率就很大”，你能有小小的头绪来把握了这个事件了 <等价于 > 这个钥匙的摆放混乱程度降低了。也就是知道一个特征属性后的信息熵是降低了。
那么知道一个特征属性的钥匙摆放情况，会给问题的信息熵减少，减少越多的特征属性，说明它是最关键的特征属性（是要找钥匙首先想起的第一个问题）

通过比较信息增益的大小，确定特征的询问决策顺序，信息增益越大，就越靠前询问决策分类，这就是ID3 决策树的核心思想。

这个思想就像你期末考试，老师给你划重点了，你是不是觉得不那么慌了，因为你知道考试的范围了，会考什么内容了，对考试把握的程度提升了。
换一句话说就是老师划的重点就是一个特征属性，你知道了，比没划重点之前更能把握期末考试了。在信息熵里面描述就是，划重点之前比划重点之后信息熵减少了，对未知的东西把握的程度提高了。

---

总结

信息量、信息熵的概念看懂后，用日常生活中例子去理解其实不并难。科学是派生出来的，是领会出来的形式化表达。