第六次CCF计算机软件能力认证 送货 (找欧拉路径)

分析

本题是判断一个无向图是否具有欧拉路径，或者欧拉回路(起点和终点相同的欧拉路径)
对于无向图：

1. 欧拉路径存在的充分必要条件：度数为奇数的点个数为2个或0个
2. 欧拉回路存在的充分必要条件：度数为奇数的点个数为0个

度数为奇数的点有2个时，起点的度数不能是偶数：

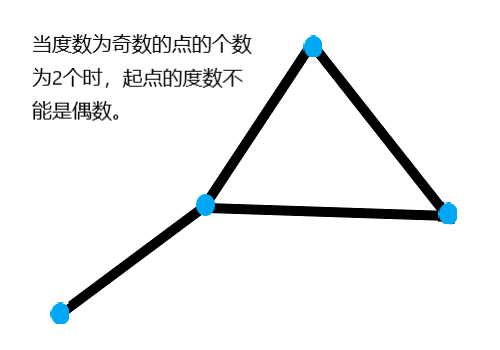
由于本题要求求出字典序最小的路口顺序(点集合)，所以需要将所有点加入到一个数组中进行排序，保证能得到最小字典序。

C++ 代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N = 1e4+10,M = 2e5+10;
int h[N],e[M],ne[M],idx;
int d[M],ans[M / 2],cnt;
int n,m;
bool used[M];
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
    vector<PII> v;  //数组v存储所有可以走的边
    for(int i=h[u];~i;i=ne[i])
    {
        if(!used[i])    //此边没有被用过
            v.push_back({e[i],i});
    }
    sort(v.begin(),v.end());    //排序，让点按大小顺序进行排列(最小字典序)
    for(auto &t :v)
    {
        if(used[t.second]) continue;
        used[t.second]=used[t.second^1]=1;  //该边和该边的反边都标记用过
        dfs(t.first);       //向下一个点j进行搜索
    }
    ans[++cnt]=u;   //当前点加入到答案中
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int a,b;
    for(int i=0;i<m;i++)
    {
        cin>>a>>b;
        add(a,b);
        add(b,a);
        d[a]++,d[b]++;  
    }
    
    int co=0;
    for(int i=1;i<=n;i++)   //计算每个点的度数
    {
        if(d[i]%2) co++;
    }
    
    //co==0位欧拉回路,co==2为欧拉路径，当co==2时，要确保起点的度数不等于偶数，不满足条件，直接输出-1
    if(co!=0 && co!=2 || (co == 2 && d[1] % 2 == 0) ){
        puts("-1");
        return 0;
    }
    dfs(1);  //根据题意，从起点1开始走
    
    if(cnt<n) {  //最终不能将所有的点走到，则输出-1
        puts("-1");
        return 0;
    }
    
    for(int i=cnt;i;i--)    //由于dfs是最后再加入当前点u的，所以最小字典序应该为逆序，所以倒着输出
        cout<<ans[i]<<" ";
    return 0;
}