PTA 7-1 最大子列和问题（C语言实现）

最新推荐文章于 2022-07-07 15:06:40 发布

原创最新推荐文章于 2022-07-07 15:06:40 发布 · 834 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #分治 #C语言

C语言同时被 2 个专栏收录

5 篇文章

订阅专栏

分治算法

2 篇文章

订阅专栏

本文解析了一种求解最大子列和问题的算法，通过分治思想在O(NlogN)的时间复杂度内找到给定序列中连续子列的最大和。介绍了算法的基本原理、递归实现方式及代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：给定K个整数组成的序列{ N1, N2 , …, NK }，“连续子列”被定义为{ Ni , Ni+1 , …, Nj }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

数据1：与样例等价，测试基本正确性；
数据2：102个随机整数；
数据3：103个随机整数；
数据4：104个随机整数；
数据5：105个随机整数；

输入格式：输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。
输出格式：在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例：
6
-2 11 -4 13 -5 -2
输出样例：20

算法解析：本题采用分治的思想进行实现。对于一个序列，我们可以将其从中间分成两个子序列，分别求左右子序列的最大子序列和，以及以分割点为基础向左右两边扩展的最大子序列和。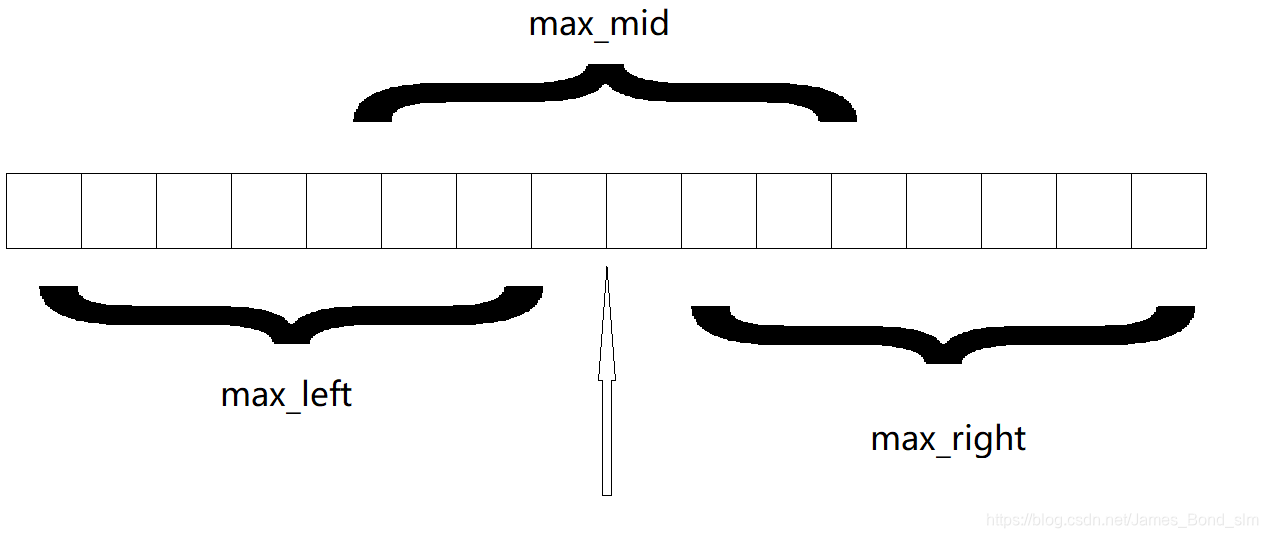只需要比较三个最大子序列和的最大值即可
那么不停的递归下去，知道左右序列都为1个，再进一步计算，求三个最大子列和的最大值返回。利用奇妙的递归和分治就能在O(NlogN)之内完成本题了

AC代码：

#include<stdio.h>

int a[100000];
int MaxSub(int a[], int begin, int end);
int max3(int a, int b, int c) 
{
	if (a>b&&a>c)
		return a;
	if (b>a&&b>c)
		return b;
	if (c>a&&c>b)
		return c;
}


int main()
{
	int k,i;
	scanf("%d",&k);
	for (i=0;i<k;i++)
	{
		scanf("%d",&a[i]);
	}
	printf("%d",MaxSub(a,0,k-1));
}


int MaxSub(int a[], int begin, int end)
{
	int mid = (begin+end)/2;
	int leftsum = 0,rightsum = 0,midsum = 0, sum = 0;
	int i;
	if (begin==end)
	{
		return a[begin];
	}
	else
	{
		// midsum
		for (i=mid;i>=begin;i--)
		{
			sum += a[i];
			if (sum>midsum) midsum = sum;
		}
		for (i=mid+1; i<=end; i++)
		{
			sum += a[i];
			if (sum>midsum) midsum = sum;
		}
		
		//leftsum
		leftsum = MaxSub(a, begin, mid);
		//rightsum
		rightsum = MaxSub(a, mid+1, end);
	}
	return (max3(leftsum, rightsum, midsum));
}