人工智能笔记08 聚类算法

简介

将数据集中的样本划分为若干个通常不相交的子集（“簇”，cluster）.

形式描述

假定样本集合D={x1，……,xm}D=\{x_1，……,x_m\}D={x1​，……,xm​}包含m个无标记样本，每个样本xi={xi1……xin}x_i=\{x_{i1}……x_{in}\}xi​={xi1​……xin​}十一i个n维得特征向量，聚类算法将样本集D划分为k个不相交的簇

{Cl∣l=1,2……k}\{C_l|l=1,2……k\}{Cl​∣l=1,2……k}
其中$C_{l^{\prime }}{\cap }_{l^{\prime }\ne l}{C}_l=\varnothing$并且$D={\cup }_{l=1}^k{C}_l$

相应地，用λj∈{1,2,……k}\lambda_j\in\{1,2,……k\}λj​∈{1,2,……k}表示样本$x_j$的簇标记（cluster label)
$x_j\in C_{\lambda }$,于是聚类结果可以用包含$m$个元素的簇标记向量λ={λ1,……λm}\lambda=\{\lambda_1,……\lambda_m\}λ={λ1​,……λm​}

• 单独过程：
Ø 用于找寻数据内在的分布特征，exploratory data analysis
• 前驱过程：
Ø 作为分类等其他学习任务的数据预处理，feature pre-processing
• 应对大数据的有效方式：
Ø 无监督方

聚类类别

按照聚类算法的主要思路
Ø 划分法（Partitioning Methods）：基于一定标准构建数据的划分。
• 属于该类的聚类方法有：k-means、k-modes、k-prototypes、kmedoids、PAM、CLARA、CLARANS等。

Ø 层次法（Hierarchical Methods）：对给定数据对象集合进行层次分解

Ø 密度法（density-based Methods）：基于数据对象的相连密度评价

Ø 网格法（Grid-based Methods）：将数据空间划分成为有限个单元（
Cell）的网格结构，基于网格结构进行聚类。

Ø 模型法（Model-Based Methods）：给每一个簇假定一个模型，然后
去寻找能够很好的满足这个模型的数据集。

Ø 基于距离的聚类算法
• 用各式各样的距离来衡量数据对象之间的相似度，如k-means、k-medoids、BIRCH、CURE等算法。

Ø 基于密度的聚类算法
• 相对于基于距离的聚类算法，基于密度的聚类方法主要是依据合适的密度函数等。如DBSCAN

Ø 基于互连性(Linkage-Based)的聚类算法
• 通常基于图或超图模型。高度连通的数据聚为一类，如复杂网络中的社团发现。

划分聚类算法

给定数据集D={x1,……,xm}D=\{x_1,……,x_m\}D={x1​,……,xm​}，k均值算法针对聚类所得的簇划分C={C1,……Ck}C=\{C_1,……C_k\}C={C1​,……Ck​}最小化平方误差

$$E=\sum _{i=1}^k\sum _{x\in C_j}||x-{\mu }_i|{|}_2^2$$
其中${\mu }_i$是簇$C_i$的均值向量
E值在一定程度上刻画了簇内样本围绕均值向量的紧密程度，E值越小，簇内样本相似度越高

1.从D中随机选择k个样本作为初始的均值向量{mu1....muk}
2.		令Ci = ∅（ 0 < i < k+1)
3.	 	for j in range(1,m+1):
4. 		计算xj到均值向量mui的距离：dji = ||xj-mui||
5. 		跟距离最近均值确定xj的簇值：lambdaj = arg min{dji}
6. 		样本 xj 划入相应的簇 C_{lambda_j} += xj(把xj放进去）
7. 	end for
8. 	
9. 	for i in range(1, k+1)
10. 		计算新均值向量 mui' = sum{x} / |Ci|				(x in Ci)
11.		if ui' != ui
12.			ui = ui'
13.		else
14.			保持
15.		end if
16.	end for
17.until  当前均值向量未更新
18.return 簇划分结果

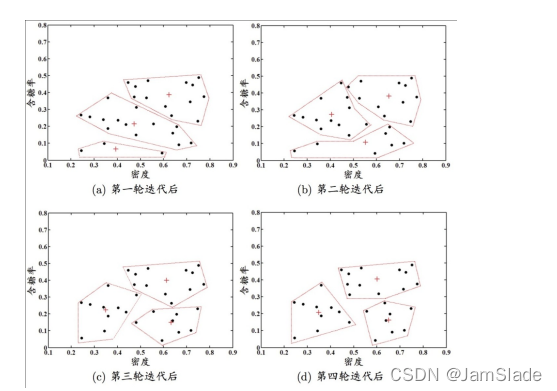
西瓜例子：
Ø 接下来以的西瓜数据集4.0为例，来演示k均值算法的学习过程。将编号
为$i$ 的样本称为 $x_i$.



• 最优性：
Ø NP难问题
Ø 贪心，依赖初始值
• 耗时：
Ø 较快停止
Ø 某些情况下复杂度高
• K值选择：
Ø Loss-k曲线
标准k-means（1957）不足：
Ø 依赖初始值、计算复杂度过高
k-means++（SODA 2007）：
Ø 初始化环节，添加seed节点迭代随机筛选
Ø 效果：
• 极大降低时间复杂度
• 提高准确度

密度聚类

• 适用场景：
Ø 聚类结构能通过样本分布的紧密程度来确定。
• 主要过程：
Ø 从样本密度的角度来考察样本之间的可连接性，
Ø 基于可连接样本不断扩展聚类簇来获得最终的聚类结果
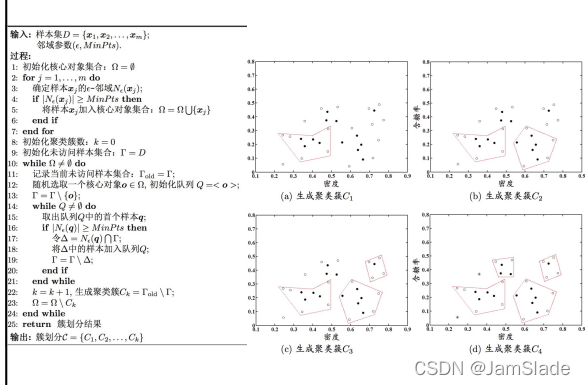
代表算法：DBSCAN

基本概念

$ϵ$邻域，对于样本$x_j\in D$他的$ϵ$邻域包含样本集D中与$x_j$的距离不大于$ϵ$的样本

核心对象：若样本$x_j$的$ϵ$邻域至少包含MinPts个样本，该样本点为一个核心对象

密度直达：若样本$x_j$位于样本$x_j$的$ϵ$邻域中，$x_j$是一个核心对象，称样本$x_j$由$x_i$密度直达

密度可达：对样本$x_i$和$x_j$，若存在样本序列$p_1,\dots \dots p_n$其中$p_1=x_i，p_n=x_j$ 并且$p_{i+1}$由$p_i$密度直达，则这两个密度可达

密度相连：对样本$x_i$和$x_j$，若存在样本$x_k$与他们密度可达，则xixj密度相连

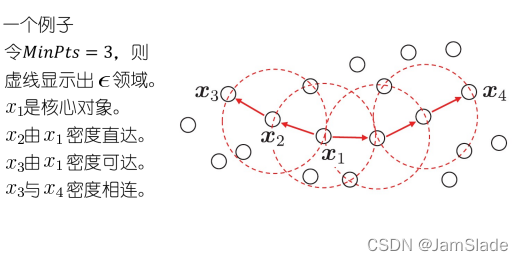
由密度可达关系导出最大密度相连样本集合

给定领域参数，簇是满足以下性质的非空样本子集
连接性：
$$x_i\in C,x_j\in C\Rightarrow x_i和x_j密度相连$$
最大性
$$x_i\in C,x_i和x_j密度可达\Rightarrow x_j\in C$$
实际上若x为核心对象，由x密度可达的所有样本组成的集合记为X={x′∈D∣x′由x密度可达}X=\{x'\in D|x'由x密度可达\}X={x′∈D∣x′由x密度可达}则X是满足连接性和最大性的簇

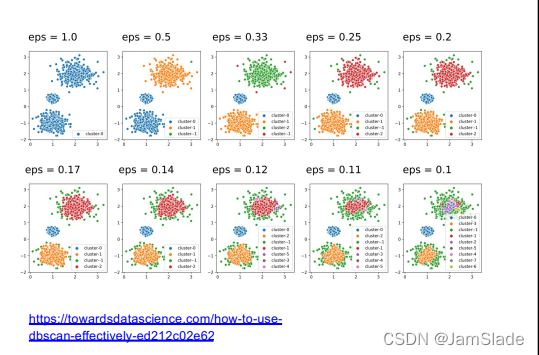
• 经典工作：
Ø KDD 1996
Ø O（n logn）复杂度
• 理论复杂度争议：
Ø SIGMOD 2015 Best Paper
Ø 实际：O（n^2) 时间复杂度
Ø Grid网格划分新方法
• 实践建议平反：
Ø TODS 2017
Ø 理论复杂度现实较为罕见
Ø 结合高效索引一起使用，
在大规模数据上，经典方
法更有优势

层次聚类

• 主要思路：
Ø 在不同层次对数据集进行划分，从而形成树形的聚类结构。
Ø 数据集划分既可采用“自底向上”的聚合策略，也可采用“自顶向下”
的分拆策略

代表算法，AGNES算法

两个聚类簇的距离度量方式
最小距离
$$d_{min}(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\min }dist(x,z)$$

最大距离
$$d_{max}(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\max }dist(x,z)$$

平均距离
$$d_{ave}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum _{x\in C_i}\sum _{z\in C_j}dist(x,z)$$

Ward距离
$$\Delta (A,B)=\sum _{i\in A\cup B}||\overrightarrow{x_i}-\overrightarrow{\underset{A}{m}}|{|}^2-\sum _{i\in B}||\overrightarrow{x_i}-\overrightarrow{\underset{B}{m}}|{|}^2=\frac{n_A{n}_B}{n_B+n_A}||\overrightarrow{\underset{A}{m}}-\overrightarrow{\underset{B}{m}}|{|}^2$$

K_means

程序主体如下所示。

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>

using namespace std;

const double eps = 1e-6;

struct Point {
    vector<double> coordinate;
    int groupId;
    /**
     * @brief 计算两个 Point 之间的欧氏距离的平方,
     *          要求两个 Point coordinate 长度相等
     */
    double distance(const Point &other) const {
        // 采用欧氏距离平方作为指标.
        double ans = 0;
        int sz = max(coordinate.size(), other.coordinate.size());
        for (int i = 0; i < sz; ++i)
            ans += (coordinate[i] - other.coordinate[i]) * (coordinate[i] - other.coordinate[i]);
        return ans;
    }
    /**
     * @brief 将另一个 Point 赋值给当前 Point
     */
    Point &operator=(const Point &other) {
        if (this == &other) return *this;
        coordinate = other.coordinate;
        groupId = other.groupId;
        return *this;
    }
    /**
     * @brief 按 coordinate 顺序比较两个 Point 的大小,
     *          要求两个 Point coordinate 长度相等
     */
    bool operator<(const Point &other) const {
        auto sz = max(coordinate.size(), other.coordinate.size());
        for (auto i = 0; i < sz; ++i)
            if (fabs(coordinate[i] - other.coordinate[i]) > eps)
                return coordinate[i] < other.coordinate[i];
        return false;
    }
};

// 你的代码会被嵌入在这

bool vectorIsEqual(const vector<Point> &centers, const vector<Point> &temp) {
    auto v1 = centers;
    sort(v1.begin(), v1.end());
    auto v2 = temp;
    sort(v2.begin(), v2.end());
    auto k = max(v1.size(), v2.size());
    for (auto i = 0; i < k; ++i)
        if (v1[i] < v2[i] || v2[i] < v1[i])
            return false;
    return true;
}

vector<Point> kMeans(vector<Point> &points, const int k) {
    vector<Point> centers(k);
    vector<Point> temp;
    for (auto i = 0; i < k; ++i)
        centers[i] = points[i];
    do {
        temp = centers;
        centers = update(points, temp);
    } while (!vectorIsEqual(centers, temp));
    return centers;
}

double score(const vector<Point> &points, const vector<Point> &centers) {
    auto n = points.size();
    auto ans = 0.0;
    for (auto i = 0; i < n; ++i)
        ans += points[i].distance(centers[points[i].groupId]);
    return ans;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    vector<int> target(n);
    vector<Point> points(n);
    for (int i = 0; i < n; ++i) {
        points[i].coordinate.resize(m);
        for (int j = 0; j < m; ++j) {
            scanf("%lf", &(points[i].coordinate[j]));
        }
        scanf("%d", &target[i]);
    }
    auto centers = kMeans(points, 2);
    printf("%f\n", (double)score(points, centers));
    return 0;
}

代码

vector<Point> update(vector<Point> &points, const vector<Point> &last)
{
    vector<Point> newest(last);
    vector<int> count;

    int lenl = last.size();
    int lenp = points.size();
    int cor_l = last[0].coordinate.size();

    //进行迭代
    //修改分组
    for(int i = 0; i < lenp; i++)
    {
        double dis = 0xffffffff;
        int id = 0;
        for(int j = 0; j < lenl; j++)
        {
            double temp = points[i].distance(last[j]);
            if(temp < dis)
            {
                dis = temp;
                id = j;
            }
        }
        points[i].groupId = id;

    }//一开始只进行迭代 就能获得6分
    //记录新的组的情况
    //清零
    
    int* cnt = new int[lenl];
    for(int i = 0; i < lenl; i++)
    {
        cnt[i] = 0;
        for(int j = 0; j < cor_l; j++)
        {
            newest[i].coordinate[j] = 0;
        }
    }//完成归零这一步能上到35分

    //更新最近点
    //每个点都加进去，并计算一个集合的数量
    for(int i = 0; i < lenp; i++)
    {
        cnt[points[i].groupId] ++;
        for(int j = 0; j < cor_l; j++)
        {
            int id = points[i].groupId;
            newest[id].coordinate[j] += points[i].coordinate[j];
        }
    }
    //相除
    for(int i = 0; i < lenl; i++)
    {
        for(int j = 0; j < cor_l; j++)
        {
         //   if(cnt[i])
                newest[i].coordinate[j] /= cnt[i];
        }
    }
    delete[] cnt;
    
    return newest;
}