线性代数(17)——坐标转换

空间的基与坐标系

坐标系是理解空间的基的一个视角，如果只到了一个坐标系也相当于知道了空间中的一组基向量。

之前的笔记中提及过，对于同一个点，在不同的基向量构成的坐标系中，其表示形式是不同的，如下图所示，

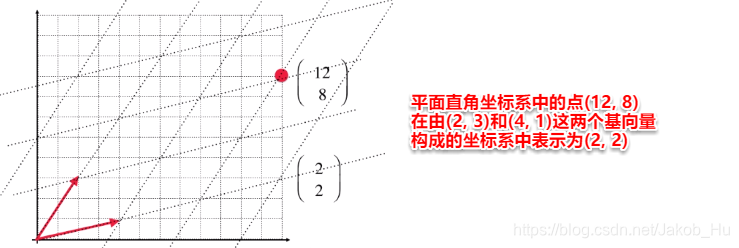
故对空间的基和坐标系之间的关系作出如下定义，

如果给定向量空间$V$在的一组基 B = { b 1 ⃗ , b 2 ⃗ , b 3 ⃗ , . . . b n ⃗ } B=\{\vec{b_1},\vec{b_2},\vec{b_3},...\vec{b_n}\} B={ b1​ ​,b2​ ​,b3​ ​,...bn​ ​}以及$V$中的一个向量$\vec{x}$，则$\vec{x}$一定可以被这组基线性表示。假设：$\vec{x}=c_1\overrightarrow{b_1}+c_2\overrightarrow{b_2}+c_3\overrightarrow{b_3}+...+c_n\overrightarrow{b_n}$，则称$\vec{x}$在这组基$B$下的坐标为$(\begin{array}{cc}{c}_1& c\end{array}$