AcWing 1073. 树的中心（树形dp）

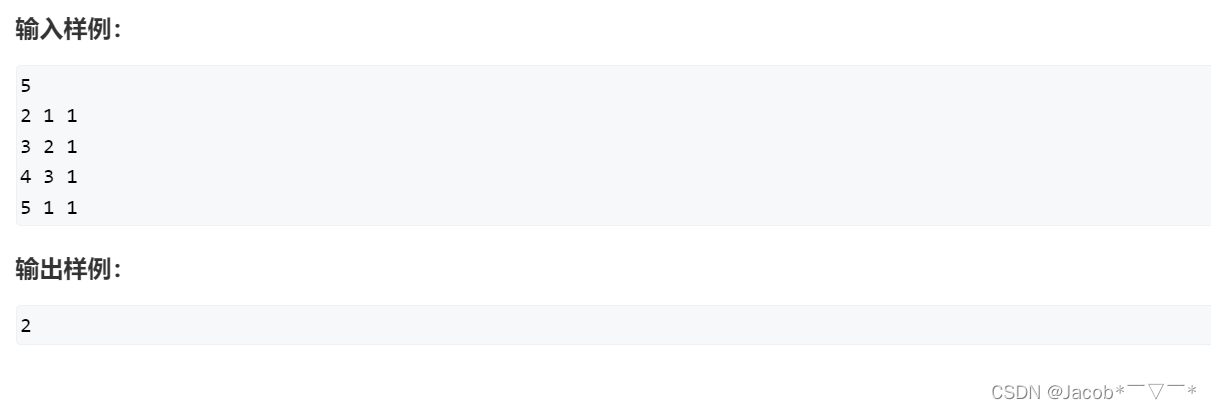
题意：

给定一棵树，树中包 含 n 个结点（编号1~n）和 n−1 条 无向边，每条边都有一个正权值。

在树中找到一个点，使得 该点到树中其他结点的最远距离最近。

思路：

我们以题目给出的样例构建一棵树：

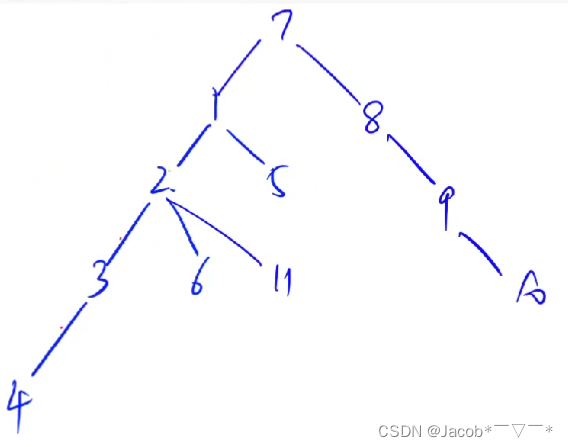
分别求出每个点到其它所有点的最长距离，在 所有距离之中取最小值

考虑一下 每个点到其它所有点距离 分为哪几类

我们可以分为 两大类，

• 第一大类：从 当前点开始往子节点走 的距离（往下）
• 第二大类：从 当前点开始往父节点走 的距离（往上）

其中第一大类可以用 上一题：AcWing 1072. 树的最长路径（树形dp） 的思路求解，我们可以先求出每个点向下走的 最大距离down1[i] 和 次大距离down2[i]

对于 第二大类情况最大值 该如何求解呢？

我们还是从 集合角度 进行分析，不妨 以树中第 2