AcWing 1294. 樱花（推公式阶乘分解运用约数个数）

Brightess

已于 2022-02-10 15:19:06 修改

阅读量459

点赞数

CC 4.0 BY-SA版权

分类专栏：数学知识文章标签：数学

于 2022-02-10 15:11:56 首次发布

本文链接：https://blog.youkuaiyun.com/Jacob0824/article/details/122861421

数学知识专栏收录该内容

38 篇文章

订阅专栏

该博客主要介绍了如何利用阶乘分解的方法解决大数模幂的问题，通过初始化素数表，进行质因数分解，然后计算每个质因数的指数并取模，最后得到结果。代码实现中，使用了O(n)的时间复杂度，适用于不超过10^6的整数范围。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述

微信图片_20220210145954.png
在这里插入图片描述

故可以利用 AcWing 197. 阶乘分解的模型了。
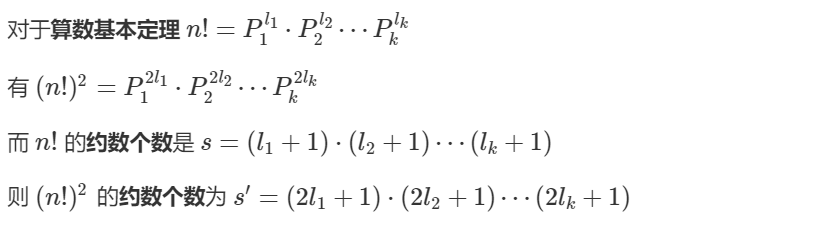
微信图片_20220210150012.png
上图转自：彩色铅笔

时间复杂度：O(n)，推导过程见AcWing 197. 阶乘分解

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int N = 1e6 + 10, mod = 1e9 + 7;

int n;
bool st[N];
int primes[N], cnt;

void init(int n) 
{
    for (int i=2; i<=n; ++i) 
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j=0; primes[j]*i<=n; ++j) 
        {
            st[primes[j]*i] = true;
            if (i%primes[j]==0) break;
        }
    }
}

signed main() 
{
    cin >> n;
    init(n);

    int res = 1;
    for (int i=0; i<cnt; ++i) 
    {
        int t = n;
        int p = primes[i];
        int s = 0;
        while(t>=1) s += t/p, t /= p;
        res = (2*s+1)*res%mod;
    }
    cout<<res<<endl;
    return 0;
}