海明码和奇偶校验码

最新推荐文章于 2025-04-20 17:00:00 发布

J_Hom832

最新推荐文章于 2025-04-20 17:00:00 发布

阅读量2.9k

点赞数 1

CC 4.0 BY-SA版权

文章标签：学习

本文链接：https://blog.youkuaiyun.com/J_Hom/article/details/126925291

海明码

能够纠正一位比特的错误。一个长度为m的数据中增

加k位冗余位，构成一个 n=m+k 位的码字，然后用 k 个监督关系式产生的 k 个校正因子来检测和纠正错误。为了能够纠正一个比特的错误，数据长度和冗余位的数目必需满足公式\ref{eq:hamming1}，海明码的编码效率效为： R=m/(m+k) 。

2k≥m+k+1 (1)

公式(1)中， m 是数据的长度， k 是海明码校验位的个数。

海明码利用监督公式对数据进行交叉校验，利用监督公式的特性可以直接定位出错数据的位置。因为二进制数据中数据的取值只有两种状态0和1，因此只要知道出错的位置，修改就变得非常的容易，只要对出错位置的数据取反就可以达到纠正的目的。例如接收端收了一串二进制数据101011，经过海明码计算后得到的数字是3，说明数据中的第3位的数据出现了错误，纠正时只需要把第三位的1取反变成0即可，纠正后的二进制串是100011。

公式(1)中海明码虽然可以实现数据的纠错，但是只能实现一个比特数据的纠错。如果数据中有多个比特同时出现错误，就必须使用更加复杂的海明公式。海明码的纠错能力和最小码距有关。

码距是编码系统中两个编码之间不同的二进制的位数，例如数据1010和数据1111的码距就是2，因为它们的第2和第3位数据不同，数据不同的位数是2，因此码距是2。最小码距（用 D 表示）是编码系统中码距的最小值。码距和纠错的能力如下：

如果要检测 e 个错误，最小码距应该满足： D>=e+1
如果要纠正 t 个错误，最小码距应满足： D>=2t+1
如果要检测 e 个错误同时纠正 t 个错误，最小码距应该满足： D>=e+t+1 , (e>=t)

本节主要讨论检测一位错误且纠正一位错误的情况，因此最小码距码距$D>=3$，需添加的冗余位的数目需满足公式(1)

校验位计算示例

已知原始数据为1001011,采用Hamming Code编码后，求实际发送的数据？

求解过程如下：

计算需要的校验位数目。从题目中可知数据为的长度为7，即 m=7 ，带入公式 m+k+1≤2k
后得到 k>=4 ，为了减少冗余$k$取最小值4。最后实际发送的数据长度为 7+4=11 位。
重新排列数据。定义4个校验位分别是 a1,a2,a3,a4 。根据海明码原则组合排列7为数据和4位校验码。校验码的位置分别是 1=20,2=21,4=22,8=23 。排列后的顺序如表1.4所示。

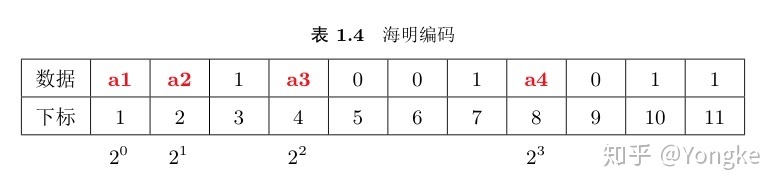
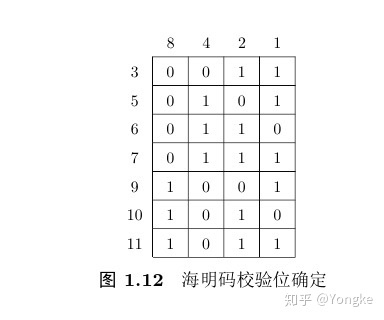
4. 计算每个校验位的值。根据图1.12所示，位置1（ 20 )，2（ 21 ），4（ 22 ），8（ 23 ）存放校验数据。在图1.12中的最后一列，列名称是1，数字3，5，7，9，11的二进制数在该列的数据为1，因此位置1对这些位置进行监督，同理，列名为2，4，8的位置对二进制数在该列为1的位置进行校验。公式1.7是海明码计算的具体公式，公式中的 X3 为表1.4中序号/下标为3的数据， X5 为表1.4中序号/下标为5的数据，其它以此类推。符号 ⊕ 表示异或运算。把表1.4中的数据带入公式(1.7)中可以得到：

a1=X3⊕X5⊕X7⊕X9⊕X11=1⊕0⊕1⊕0⊕1=1a2=X3⊕X6⊕X7⊕X10⊕X11=1⊕0⊕1⊕1⊕1=0a3=X5⊕X6⊕X7=0⊕0⊕1=1a4=X9⊕X10⊕X11=0⊕1⊕1=0 (1.7)

5. 带入校验数据得到发送数据。把 a1,a2,a3,a4 分别带入表1.4中，得到一个新的数据序列 10110010011，这个新序列就是发送端发送出去的数据，也是线路上传输的数据。如果数据没有发生冲突，这也将是接收方收到的数据。