[課程筆記] 機器學習基石 - W6. Theory of Generalization

目录

Video1: Restriction of Break Point

The Four Break Points 

Restriction of Break Point

Video2: Bounding Function: Basic Cases

Bounding Function

Table of Bounding Function

Video3: Bounding Function: Inductive

Achieving Dichotoies of B(4, 3)

Reorganized Dichotomies of B(4,3)

Putting It All Together

Bounding Function: The Theorem

Video4: A Pictorial Proof

Bad Bound for General H

Step 1、把 E_out 换掉

Step 2. Decompose H by Kind

Step 3. Use Hoeffding without Replacement

That's All

参考

---

Video1: Restriction of Break Point

The Four Break Points 

• 在上一节课中，找到了4种 hypothesis 的 break point
• 当 k 是 break point，则 k+1 也会是 break point

Restriction of Break Point

• 此处试图找出一些 break point 的特性
• 以任意的 hypothesis 为例
  • N=1 : 
  • N=2 : 
  • N=3 :  (可以透过随意取两个点无法 shatter 推导出来)
•  发现 break point 的存在，大大降低  增长速度

Video2: Bounding Function: Basic Cases

Bounding Function

• 定义 Bounding Function, B(N,k) 为:
  • 在 break point=k 时，最大的 
• Bounding Function 只与 N, k 有关，与 hypothesis 种类无关，可套用至任何 H 上

Table of Bounding Function

• 根据目前已知，填写 B(N,k) 表格:
  • B(N, k) = 1 当 k = 1
  • B(N, k) = 2 当 N = 1
  • B(N, k) = 当 N = k
• 剩下一半还无法填入，后面课程会说明

Video3: Bounding Function: Inductive

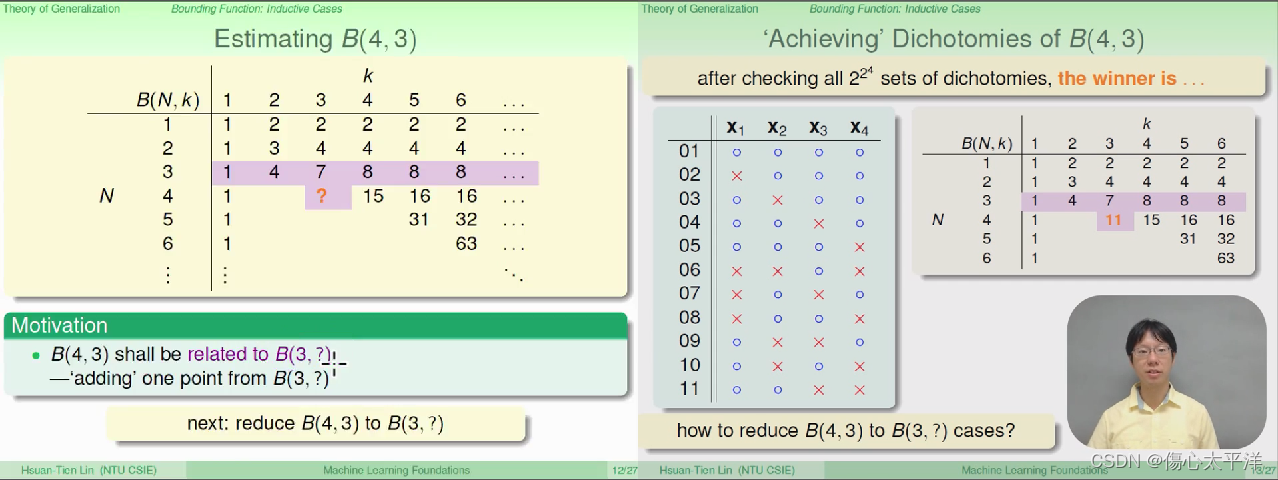
Achieving Dichotoies of B(4, 3)

• 推测 B(4, 3) 可能可以从 B(3, 3) 计算得出
• 首先使用程式自动计算 B(4, 3) = 11

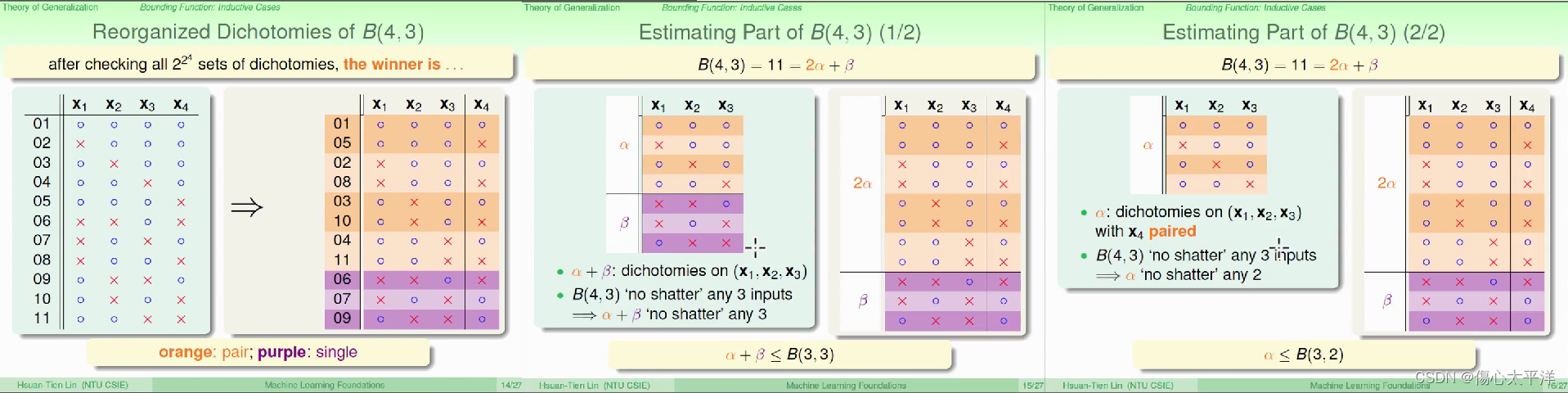
Reorganized Dichotomies of B(4,3)

• 把 B(4,3) 中所有的 dichotomies 列出来，按解的前四个结果是否成对，分成  两类
• 如果把 x1, x2, x3 取出
  • 则 dichotomies 必须满足 k = 3 的限制，也就是 
• 如果把  中的 x1, x2, x3 取出
  • 则 dichotomies 必须满足 k = 3 的限制，也就是 

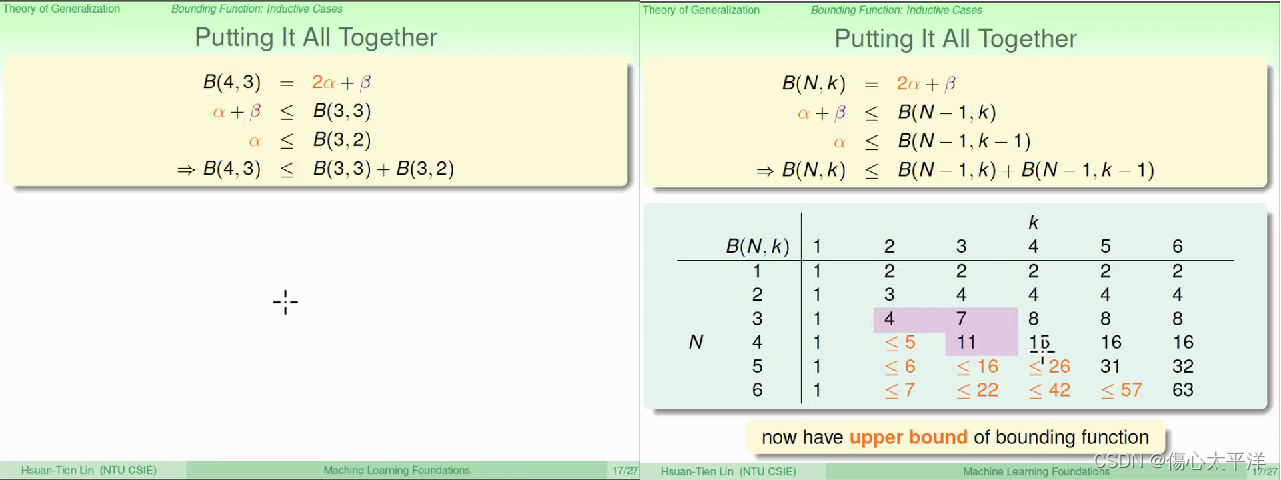
Putting It All Together

• 获得了 Bounding Function 的上限
  • 从前面的结果，可以拓展至  B(N, k) ≦ B(N-1, k) + B(N-1, k-1)
• 刚刚填到一半的表，虽然不知道值，但能知道其上限

Bounding Function: The Theorem

• 可以证明当 break point 存在时， Bounding Function 有上限 (详细证明课堂中没说明，可以自己试试看)
• 上限形式是 N 的多项式 ​​​​

Video4: A Pictorial Proof

Bad Bound for General H

• 在前面的课程，介绍了 growth function，并且知道其上限为 bounding function
• 事实上，并无法直接将霍夫丁不等式中的 M 替换成 growth function，需要进行一些修正
• 详细证明不细讲，接下来只说明这些修正的来源

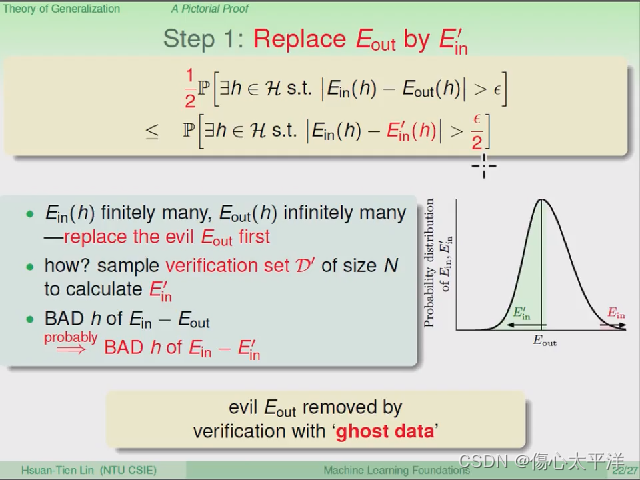
Step 1、把 E_out 换掉

• 以一个 h 的情况下来看坏事发生的几率
•  的输出集合是有限大小，但  的输出集合是无限大小
• 可以用验证集 D' 计算 ，并用 取代  得到一个上限

Step 2. Decompose H by Kind

• 现在考虑存在多种 h 的情况，坏事发生的几率
• 因为数据数量为 2N，所以最多只有  种 dichotomies
• 使用 Union bound，得到在多种 h 的情况下的上限

Step 3. Use Hoeffding without Replacement

• 在 h 数量有限的条件下，必须使用另一种 Hoeffding Inequality
• 最后可以得到坏事发生的几率的上限

That's All

• 前面的式子称为 Vapnik-Chervonenkis bound (VC bound)，说明了坏事发生几率的上限
• 可以用此式子，证明对于 2D perceptron，只要取样数够大，
• PLA 是可行的，可以学习到东西

参考

1. 機器學習基石上 (Machine Learning Foundations)---Mathematical Foundations | Courser