[課程筆記] 機器學習基石 - W9. Linear Regression

目录

Video1: Linear Regression Problem

Linear Regression Hypothesis

Illustration of Linear Regression

The Error Measure

Video2: Linear Regression Algorithm

Matrix Form of Error

Optimal Linear Regression Weights

Video3: Generalization Issue

Is Linear Regression a Learning Algorithm?

Benefit of Analytic Solution

The Learning Curve

Video4: Linear Regression for Binary Classification

Linear Classification vs. Linear Regression 

参考

---

Video1: Linear Regression Problem

Linear Regression Hypothesis

• 以信用卡申請額度為例，我們可以將每個特徵乘上一個"重要性分數"來做預測
• Hypothesis 類似前面的 perceptron，但這邊我們取的不是符號，而是數值

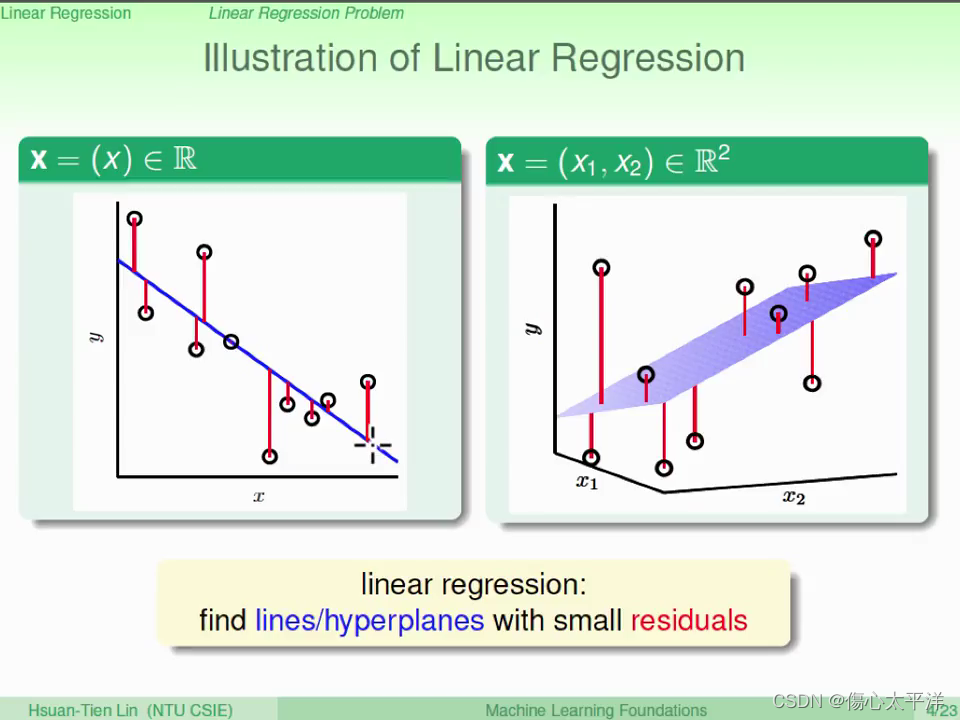
Illustration of Linear Regression

• O 代表的是實際的數據點
• 藍色線，表示的是輸入 x 得到的 y 預測值
• 目標: 找出藍色線，使數據點與線的誤差 (residual) 最小

The Error Measure

• 常用的衡量方法: squared error (SE)

---

Video2: Linear Regression Algorithm

Matrix Form of Error

• 將誤差的公式，使用矩陣形式表示，方便後續運算
• 因為誤差函數是凸函數，可以透過倒數為零來求出最佳解

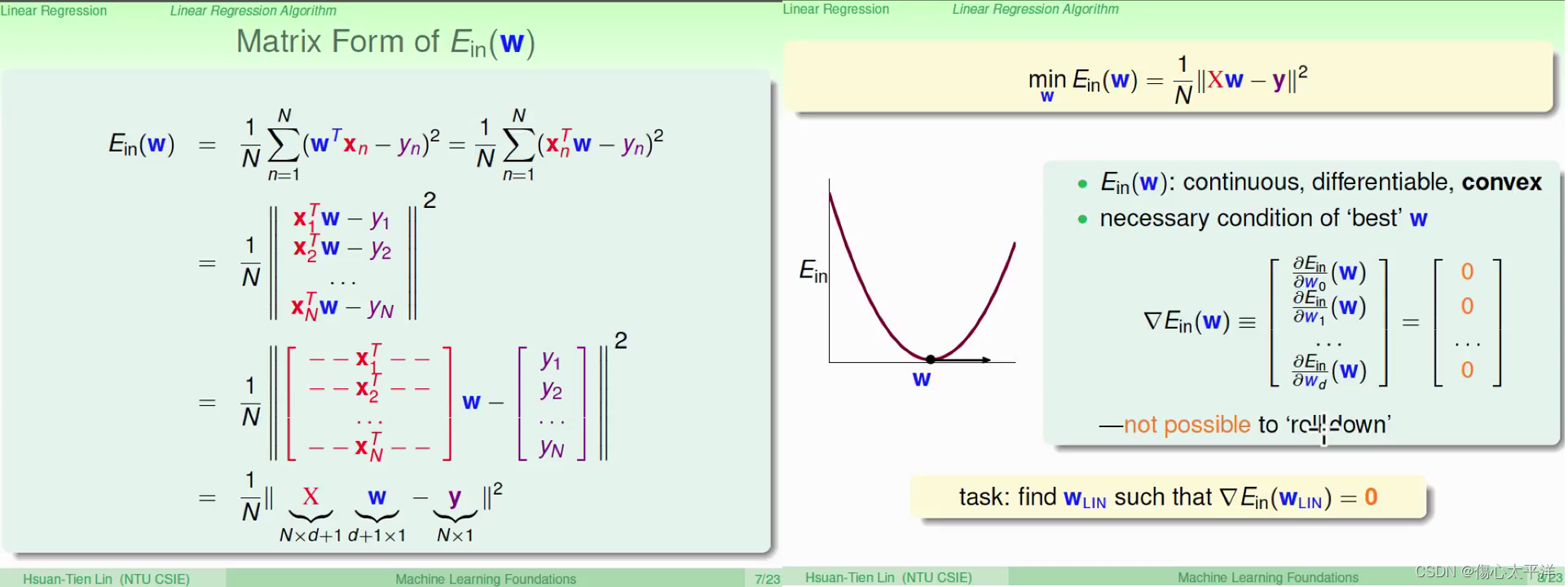
Optimal Linear Regression Weights

• 因為 N >> d+1，所以大部分情況下  是可逆的，可以計算得到 w
• 當  為奇異矩陣時，表示存在多組解，而使用 pseudo-inverse 可以得到其中一組
• 建議使用工具來求 pseudo-inverse ，而不要自己直接求解  (計算上較複雜)

---

Video3: Generalization Issue

Is Linear Regression a Learning Algorithm?

• 線性回歸俱備解析解的特性，會讓人覺得沒有學習過程
• 事實上，算法過程中包含了許多迭代計算 (如矩陣求逆等等)
• 只要  變小了，就算是有學習

Benefit of Analytic Solution

• 想知道平均樣本誤差  與那些東西有關
• Hat Matrix, H 
  • 因為 y 呈上此矩陣後等於 ，故稱為 Hat Matrix
  •  可以被視為是，令 y 在 x 的 span 中進行投影 (尋找最接近的向量)
  • (I-H) 用來計算垂於x 的 span 方向的投影
• 考慮雜訊
  • y : 輸入 x 經過理想函數 f(x) 後，加上一雜訊得到
  • 將雜訊透過 (I-H) 轉換後，會等於 

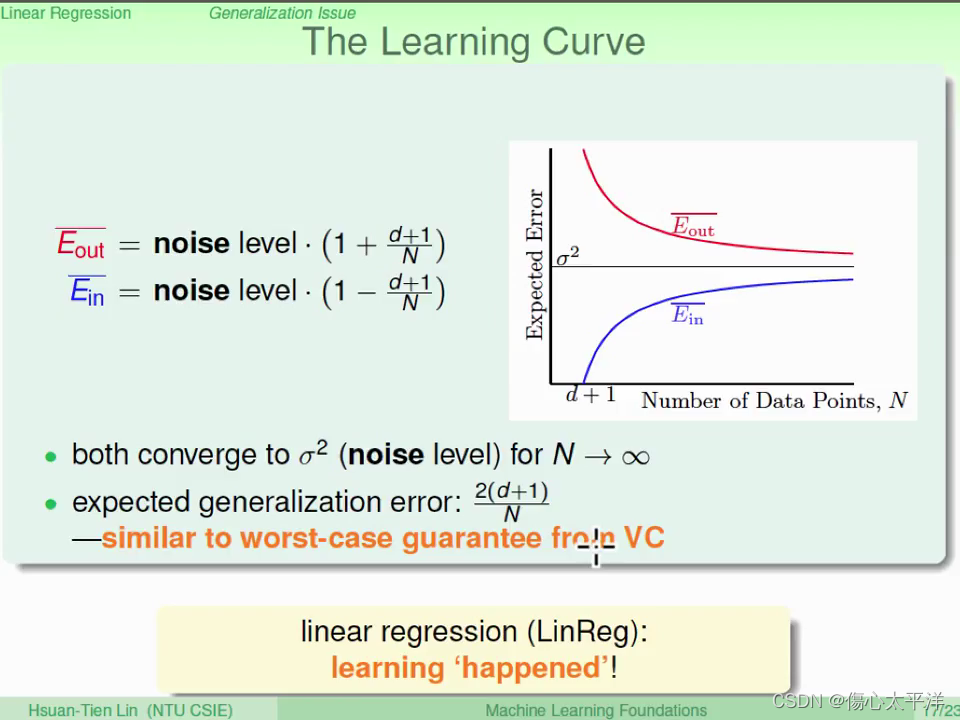
The Learning Curve

• 隨著數據量增加，平均誤差都會逐漸變小 --> 學習發生了

---

Video4: Linear Regression for Binary Classification

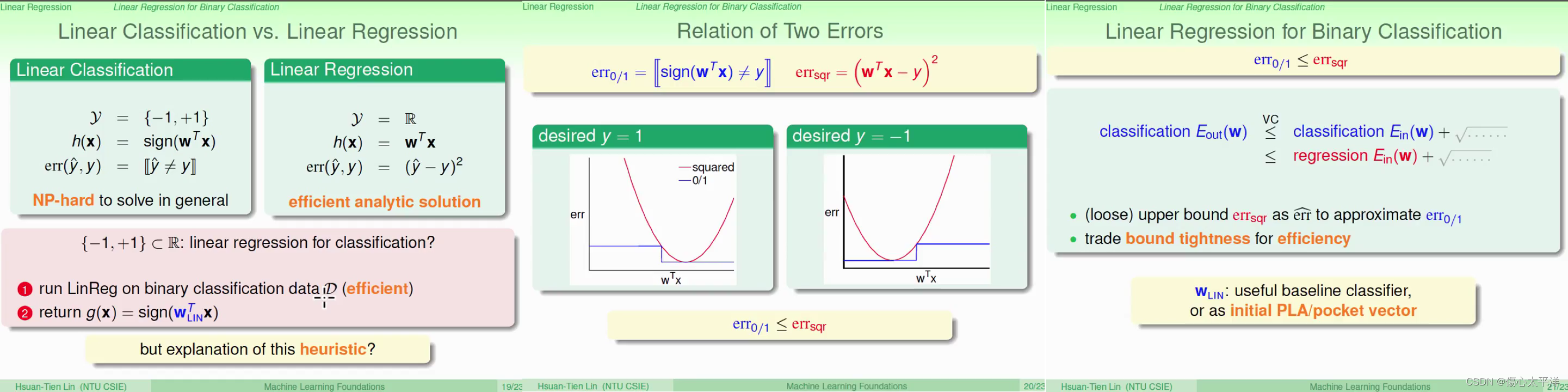
Linear Classification vs. Linear Regression 

• 兩種模型其中一個差異是誤差計算 → 
• 使用 Linear Regression 作為 Linear Classification 會發生什麼事 ?
  • Linear Regression 的樣本誤差，相較於 Linear Classification 是一個比較寬鬆的
  • 可以得到還可以的解
  • 因為求解相對有效率，所以可以用來做 PLA 的初始值

---

参考

1. 機器學習基石上 (Machine Learning Foundations)---Mathematical Foundations | Courser