Leetcode每日打卡第17天

题目

3242. 设计相邻元素求和服务

给你一个 n x n 的二维数组 grid，它包含范围 [0, n2 - 1] 内的不重复元素。

实现 neighborSum 类：

• neighborSum(int [][]grid) 初始化对象。
• int adjacentSum(int value) 返回在 grid 中与 value 相邻的元素之和，相邻指的是与 value 在上、左、右或下的元素。
• int diagonalSum(int value) 返回在 grid 中与 value 对角线相邻的元素之和，对角线相邻指的是与 value 在左上、右上、左下或右下的元素。

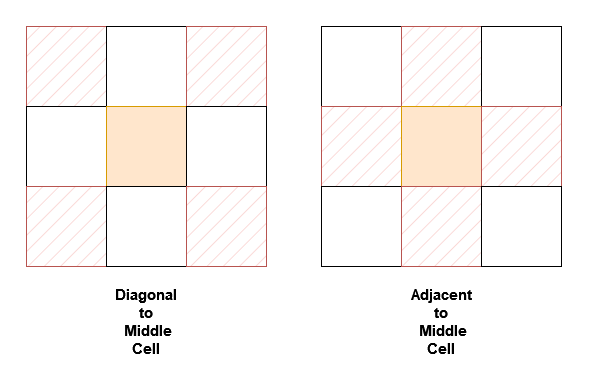
示例 1：

输入：

["neighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

输出： [null, 6, 16, 16, 4]

解释：

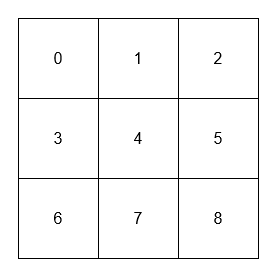
• 1 的相邻元素是 0、2 和 4。
• 4 的相邻元素是 1、3、5 和 7。
• 4 的对角线相邻元素是 0、2、6 和 8。
• 8 的对角线相邻元素是 4。

示例 2：

输入：

["neighborSum", "adjacentSum", "diagonalSum"]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

输出： [null, 23, 45]

解释：

• 15 的相邻元素是 0、10、7 和 6。
• 9 的对角线相邻元素是 4、12、14 和 15。

提示：

• 3 <= n == grid.length == grid[0].length <= 10
• 0 <= grid[i][j] <= n2 - 1
• 所有 grid[i][j] 值均不重复。
• adjacentSum 和 diagonalSum 中的 value 均在范围 [0, n2 - 1] 内。
• 最多会调用 adjacentSum 和 diagonalSum 总共 2 * n2 次。

思路

思路与算法

由于询问时给定的是元素而不是元素在二维数组中的位置，因此在初始化时，我们可以使用一个哈希表 pos 存储每一个元素所在的位置：pos 中的每个键表示一个元素，对应的值是一个二元组，表示其在二维数组中的位置。

同时，在初始化时，我们存储给定的二维数组 grid 的一份拷贝。这样一来，在查询操作 adjacentSum(value) 和 diagonalSum(value) 中，我们首先通过 pos 获取 value 的位置，随后根据查询的类型，返回四个相邻元素的和即可。

细节

为了防止重复编写代码，可以使用一个辅助函数 getSum(value,idx)，其中 idx=0 表示相邻，idx=1 表示对角线相邻。

python3代码

class NeighborSum:
    dirs = [
        [(-1, 0), (1, 0), (0, -1), (0, 1)],
        [(-1, -1), (-1, 1), (1, -1), (1, 1)],
    ]

    def __init__(self, grid: List[List[int]]):
        self.pos = dict()
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                self.pos[grid[i][j]] = (i, j)
        self.grid = grid

    def adjacentSum(self, value: int) -> int:
        return self.getSum(value, 0)

    def diagonalSum(self, value: int) -> int:
        return self.getSum(value, 1)
    
    def getSum(self, value: int, idx: int) -> int:
        x, y = self.pos[value]
        ans = 0
        for (dx, dy) in NeighborSum.dirs[idx]:
            nx, ny = x + dx, y + dy
            if 0 <= nx < len(self.grid) and 0 <= ny < len(self.grid[0]):
                ans += self.grid[nx][ny]
        return ans