神经网络：LeNet-5解析

一： 卷积神经网络（CNN: Convolutional Neural Network）

       CNN是由一个或多个卷积层和顶端的全连通层组成，同时也包括关联权重和池化层等。下图就是一个经典的神经网络。

       卷积层：卷积层是卷积神经网络的核心层，而卷积（Convoltuion）是卷积层的核心。卷积运算就是用卷积分别乘以输入张量中的每一个元素，然后输出一个代表每个输入信息的张量。其中卷积核（Kernel） 又被称为权重过滤器，简称为过滤器（Fliter）。

 

       卷积计算公式:

• H：图片高度
• W:  图片宽度
• D：原始图片通道数，也是卷积核个数
• F： 卷积核高宽大小，一般取1*1，3*3，5*5，7*7等
• P：图像边填充大小或者零填充
• S：滑动步长

      则经过本层卷积运算后的输出即下一层的输入为：

• H1 = ( H-F+2P ) / S +1
• W1= ( W-F+2P ) / S +1
• D1 = F

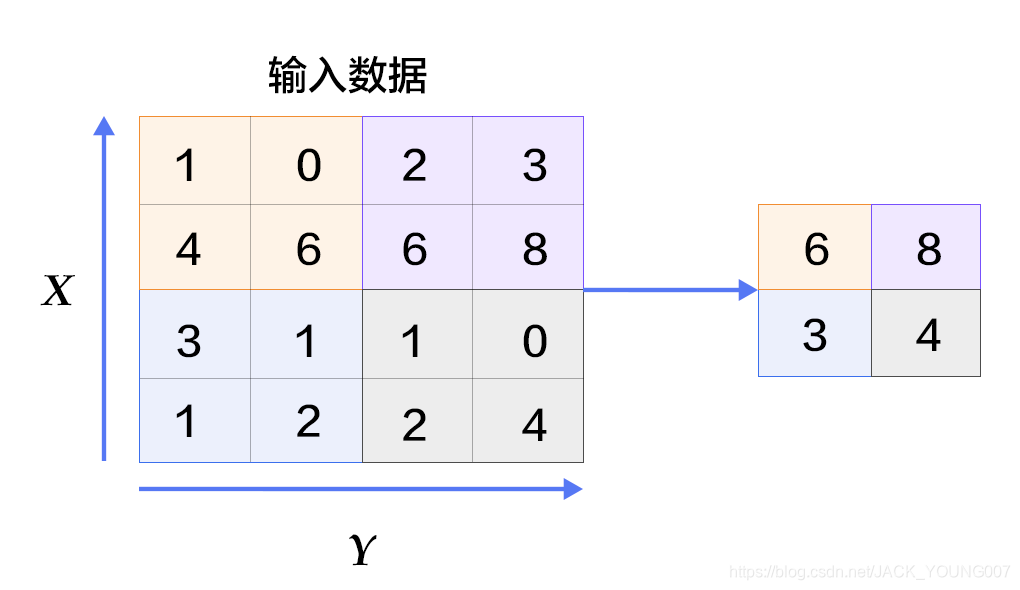
       池化层：池化（Pooling）又称下采样（Subsampling）。池化层在CNN中可用来减少尺寸、提高运算速度及减少噪声影响，让葛特征更具有健壮性。通常在卷积层的后面会加上一个池化层。池化的方式通常有三种：最大池化（MaxPooling）;均值池化（MeanPooling）;随机/概率池化。下图为最大池化示例：

Max Pooling

      激活函数：（Activation Function）就是对神经网络中某一部分神经元的非线性运算，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。激活函数一般要求可微，且不改变输入数据的维度。常见的激活函数有：Sigmoid函数、tanh函数、relu函数、softplus函数、dropout函数等。

       代价函数：代价函数是神经网络模型的效果评估及优化的目标函数，常用于监督学习中关于分类模型和回归模型中迭代优化。分类问题中常用交叉熵（cross_entropy）算法，回归问题常用误差评估（mean_squared_error）算法。

 

二 ：CNN 之 LeNet-5 模型

         CNN 模型有很多变种，LeNet-5 模型就是比较有代表性的模型。

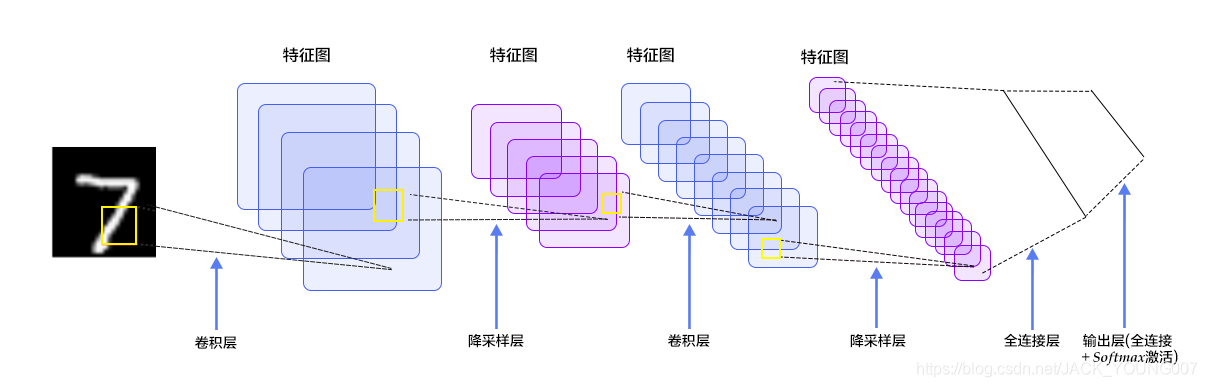
         LeNet-5 模型结构为输入层--卷积层--池化层--卷积层--池化层--全连接层--全连接层--输出层，为串联模型。如下图所示：