剑指10 - 斐波那契数列

tip

关于求余
$$(x+y)\odot p=(x\odot p+y\odot p)\odot p$$防止x+y时溢出，$\odot$是求余操作

第一种写法 ： 直接递归

int fib(int n) {
        if(n==0) return 0;
        else if(n==1) return 1;
        else return (fib(n-1)%1000000007+fib(n-2)%1000000007)%1000000007;
    }

缺点：重复计算，时间复杂度：$O(2^n)$

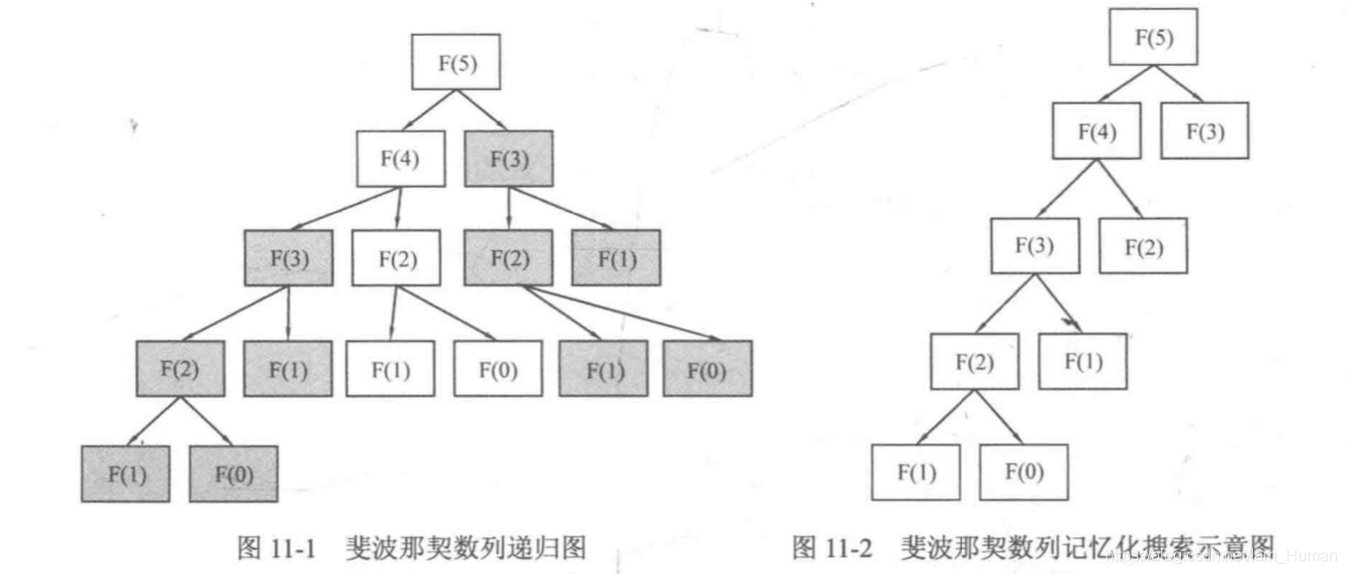
第二种写法：动态规划/记忆搜索

时间复杂度:$O(n)$, 空间复杂度:$O(n)$

int fib(int n) {
        vector<int> vi;
        for(int i=0; i<n+1; i++){
            if(i==0) vi.push_back(0);
            else if(i==1) vi.push_back(1);
            else vi.push_back((vi[i-1]%1000000007+vi[i-2]%1000000007)%1000000007); //防止溢出
        }
        return vi[n];
    } 

时间复杂度:$O(n)$, 空间复杂度:$O(1)$

int fib(int n) {
        if(n==0) return 0;
        else if(n==1) return 1;
        else{
            int p = 0;
            int q = 1;
            int temp;
            for(int i=2;i<n+1;i++){
                temp = q;
                q = (p%1000000007 + q%1000000007)%1000000007;
                p = temp;
            }
            return q;
        }
    }

第三种写法：乘方法

应用：青蛙跳台阶

考虑：设dp[n]表示跳上第n阶台阶有几种跳法，则满足动态转移方程：
$$dp[n]=dp[n-1]+dp[n-2]$$即，第n阶的跳法等于第n-1阶(再跳1阶)的跳法加上n-2阶(再跳两阶)的跳法

int numWays(int n) {
        if(n==0) return 1;
        else if(n==1) return 1;
        else{
            int p=1;
            int q=1;
            int temp;
            for(int i=2;i<n+1;i++){
                temp = q;
                q = (p%1000000007 + q%1000000007)%1000000007;
                p = temp;
            }
            return q;
        }
    }

跳台阶还可以继续延伸：一次可以跳1阶，2阶，3阶…

然后有的台阶还有破损，不能跳到上面只能跳过去…（老街）

应用2:小矩形覆盖大矩形

用21的小矩形无重叠的覆盖2n的大矩形，覆盖规律满足：
f(n)=f(n-1)+f(n-2)