#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1000;
const int INF = 10000000;
int n, m, s, G[MAXN][MAXN];//n是顶点个数,m是边数,s是起点的编号,G数组是储存两个顶点之间的边权
int d[MAXN];//存放每个节点到起点的最短距离
bool vis[MAXN] = { false };//表示这个点是否已经走过了
void Dijstra1(int s)
{
fill(d, d + MAXN, INF);
d[s] = 0;
for (int i = 0; i < n; i++)
{
int u = -1, MIN = INF;
for (int j = 0; j < n; j++)//这个循环用来寻找还没有走到过的结点中距离原点最小的点
{
if (vis[j] == false && d[j] < MIN)//如果这个点没走过并且是最短值
{
u = j;
MIN = d[j];
}
}
if (u == -1)
return;
vis[u] = true;
for (int v = 0; v < n; v++)//循环所有从上面找出来的结点u可以走到的所有结点
{
if (vis[v] == false && G[u][v] != INF && d[u] + G[u][v] < d[v])//如果这个结点还没有走过而且可以从u结点走到,并且可以进行优化
{
d[v] = d[u] + G[u][v];//优化d[v],更新这个最小值
}
}
}
}
int main()
{
int hasDirect;
cout<<"请选择有向图/无向图: 无向图:0, 有向图:1"<<endl;
cin>>hasDirect;
int u, v, w;
cout<<"请输入顶点个数,边的个数,起点编号(从0开始)"<<endl;
cin >> n >> m >> s;//顶点个数,边数,起点编号
fill(G[0], G[0] + MAXN * MAXN, INF);
cout<<"依次输入各边的权,无向图的边(u, v)与有向图的边<u, v>均按照 u v w 的格式输入:"<<endl;
for (int i = 0; i < m; i++)
{
cin >> u >> v >> w;//输入相通的两个定点u和v之间的边权
if(hasDirect==0){
G[u][v] = w;
G[v][u] = w;
}
else G[u][v] = w;
}
Dijstra1(s);
for (int i = 0; i < n; i++)
{
cout<<"从第"<<s<<"点至"<<i<<"点的最短距离(1000代表不可达)为:"<< d[i]<<endl;
}
// system("pause");
return 0;
}
无向图:
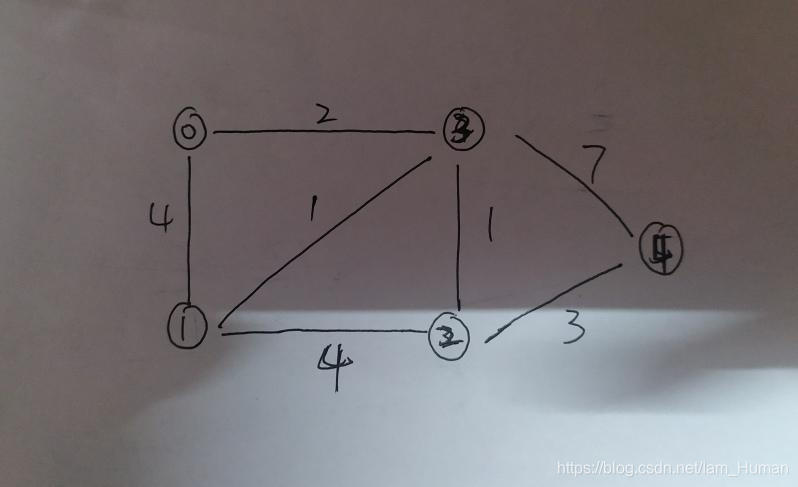

有向图:
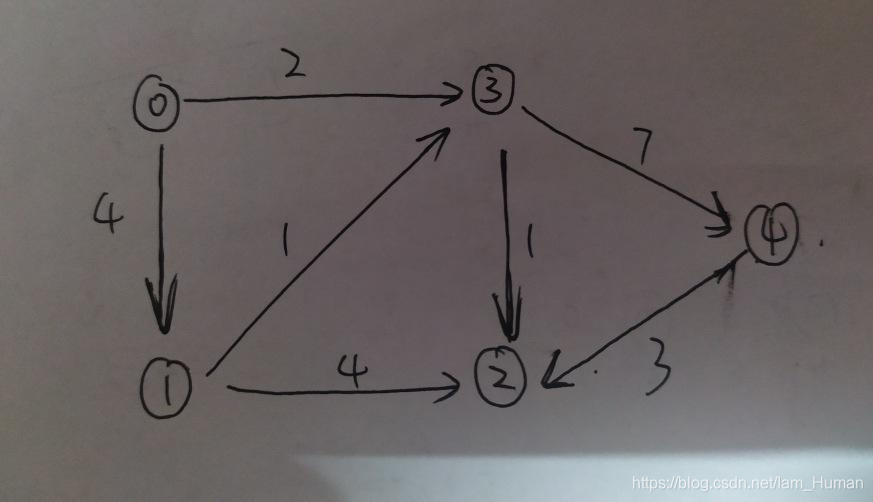






 本文深入讲解了Dijkstra算法,一种用于解决带权图中单源最短路径问题的经典算法。通过详细代码解析,展示了如何使用C++实现Dijkstra算法,包括初始化、选择最短路径节点及更新邻居节点距离的过程。适合于对图论和算法有兴趣的学习者。
本文深入讲解了Dijkstra算法,一种用于解决带权图中单源最短路径问题的经典算法。通过详细代码解析,展示了如何使用C++实现Dijkstra算法,包括初始化、选择最短路径节点及更新邻居节点距离的过程。适合于对图论和算法有兴趣的学习者。
















 4541
4541

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








