2 计算可解性与渐近阶

计算可解性

许多问题的一个共性：离散特性。它们都与大量组合可能性上的隐含搜索相关，目标将是高效率地找到一个解，而这个解满足某些被清晰描述的条件
对其中的大多数问题，都存在一个明显的蛮力搜索，即尝试所有的可能性看其中是否有合格的

效率定义1 当实现一个算法时，如果他在真实的输入实例上运行得快，那么这个算法是有效的

效率定义2 在分析的层次上，如果一个算法与蛮力搜索比较，最坏情况下达到质量上更好的性能，就说它是有效的

效率定义3 如果一个算法有多项式运行时间， 它就是有效的

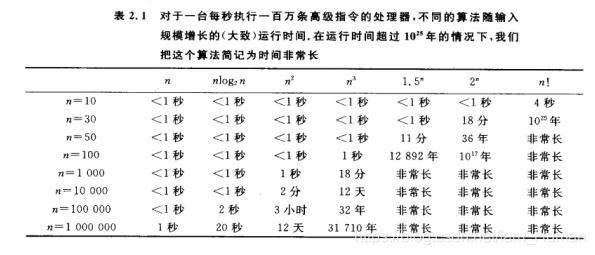
增长的渐近阶

一步： 当考察计算抽象的不同层次， 一步的概念可以增大或缩小一个常数因子

T(n): 函数-在规模为n的输入上最坏的运行时间
f(n): 函数

对充分大的n, 函数T(n)不超过f(n)的常数倍，就说T(n)是O(f(n))的，读作T(n)是f(n)阶的, f是T的渐近上界
$$T(n)=O(f(n))\iff \forall n\ge n_0,T(n)\le c\ast f(n)$$

对充分大的n, 函数T(n)至少是某个特定函数f(n)的常数倍，f是T(n)的渐近下界
$$T(n)=\Omega (f(n))\iff \forall n\ge n_0,T(n)\ge \epsilon \ast f(n)$$

一个函数可能有许多个上界
$$T(n)=O(n^2)=O(n^3)$$

f(n)即是T(n)的渐近上界， 又是T(n)的渐近下界， 则f是T(n)的渐近的紧的界
$$\begin{gathered} T(n)=\Omega (f(n))\wedge T(n)=O(f(n))\iff T(n)=\Theta (f(n)) \\ \underset{x\to 0}{\lim }\frac{f(n)}{g(n)}=c>0\iff T(n)=\Theta (f(n)) \end{gathered}$$
\\ \\ \\

渐近增长率的性质

传递性 如果f=O(g) 且 g=O(h) , 那么f=O(h) （渐近下界，渐近的紧的界同理)

函数的和 如果f=O(h) 且 g=O(h) 那么 f+g = O(h) (可推广至多个函数相加)

假设f 和g 是两个函数(取非负的值) , 满足g = O(f) , 那么f+g= (f) 换句话说f是一个关于f+g的渐近的紧的界、

多项式的渐近界 令f是一个d阶多项式， d次方的系数a是正数， 那么$$f=O(n^d)$$
底数函数的渐近界 当a>1， 对任意x>0， 有
$$lo{g}_{a}n=O(n^2)$$

指数函数的渐近界 当d>0, 对任意r>1, 有
$$n^d=O(r^n)$$