机器学习-K-Means算法

最新推荐文章于 2025-10-08 13:50:15 发布

原创

最新推荐文章于 2025-10-08 13:50:15 发布 · 1k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#聚类 #列表 #算法 #机器学习

K-Means是一种非监督学习中的聚类算法，通过迭代寻找簇的质心来实现数据划分。该算法简单易懂，目标是最小化各点到其所在簇质心的距离平方和。虽然算法时间复杂度较高，为O(nkt)，但它在许多场景下仍能有效工作。代码已上传至GitHub供测试和学习。

简介
又叫K-均值算法，是非监督学习中的聚类算法。

基本思想
k-means算法比较简单。在k-means算法中，用cluster来表示簇；容易证明k-means算法收敛等同于所有质心不再发生变化。基本的k-means算法流程如下：

选取k个初始质心（作为初始cluster，每个初始cluster只包含一个点）；  
repeat：  
        对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster；  
        重新计算k个cluster对应的质心（质心是cluster中样本点的均值）；  
until 质心不再发生变化

repeat的次数决定了算法的迭代次数。实际上，k-means的本质是最小化目标函数，目标函数为每个点到其簇质心的距离的平方和：
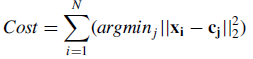
在这里插入图片描述
N是元素个数，x表示元素，c(j)表示第j簇的质心

即：
初始化选择 k 个质心 (随机选择, 或者领域知识选择), 该选择决定了聚类的速度与效果
为所有点划分簇
计算该种划分的损失
当该损失还能减小时循环以下:
对于每个质心(k个)执行:
a. 随机选择一个新的点
b. 以新的点代替这个质心
c. 重新对所有数据划分簇
d. 计算划分的损失
e. 若 新的损失小于原先的损失, 则 用新的点代替原质心

算法复杂度
时间复杂度是O(nkt) ,其中n代表元素个数，t代表算法迭代的次数，k代表簇的数目

优缺点

优点
简单、快速；
对大数据集有较高的效率并且是可伸缩性的；
时间复杂度近于线性，适合挖掘大规模数据集。
缺点
k-means是局部最优，因而对初始质心的选取敏感；
选择能达到目标函数最优的k值是非常困难的。

代码
代码已在github上实现，这里也贴出来

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt


def loadDataSet(fileName):
    '''
    加载测试数据集，返回一个列表，列表的元素是一个坐标
    '''
    dataList = []
    with open(fileName) as fr:
        for line in fr.readlines():
            curLine = line.strip().split('\t')
            fltLine = list(map(float,curLine))
            dataList.append(fltLine)
    return dataList


def randCent(dataSet, k