机器学习-多元线性回归（multiple linear regression）

最新推荐文章于 2025-08-10 22:38:56 发布
原创 最新推荐文章于 2025-08-10 22:38:56 发布 · 5.1k 阅读 · 23 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #机器学习 #深度学习 #线性代数 #算法

本文介绍了多元线性回归的概念，包括单变量、多变量及多项式回归，并通过Python进行数据导入与分析。利用数据展示了单变量线性回归的散点图，计算了相关系数，接着进行了训练集与测试集的划分，最后实施了多变量线性回归模型的训练，得出最佳拟合线。

先甩几个典型的线性回归的模型，帮助大家捡起那些年被忘记的数学。

● 单变量线性回归： h(x)=theta0 + theta1* x 1
● 多变量线性回归： h(x)=theta0 + theta1* x 1 + theta2* x 2 + theta3* x 3
● 多项式回归： h(x)=theta0 + theta1* x 1 + theta2* (x2^2) + theta3* (x3^3)

多项式回归始终还是线性回归，你可以令x2=x22，x3=x33，简单的数据处理一下就好了，这样上述多项式回归的模型就变成多变量线性回归的模型了。

数据导入
下面我们要开始用数据说话了，先来看看数据源是什么样子吧。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression

#读取文件
datafile = u'E:\\pythondata\\dhdhdh.xlsx'#文件所在位置，u为防止路径中有中文名称，此处没有，可以省略
data = pd.read_excel(datafile)#datafile是excel文件，所以用read_excel,如果是csv文件则用read_csv
examDf = DataFrame(data)
examDf.head()

运行结果：

 Call   Connect    Return

0 2.1335 1.267760 1.176615
1 2.5534 1.352941 1.978967
2 3.3361 1.872093 2.249511
3 3.3861 1.826667 2.986597
4 3.9682 1.875000 2.798570

单变量线性回归

绘制散点图
先将上述数据中的Connect（接通量）和Return（回款量）做一个单变量的线性回归，先绘制一个散点图，大致看一下分布情况。

#绘制散点图,examDf.jt为X轴，examDf.hk为Y轴
plt.scatter(examDf.Connect,examDf.Return,color = 'darkgreen',label = "Exam Data")
 
#添加图的标签（x轴，y轴）
plt.xlabel("The Connection amount of the average account")#设置X轴标签
plt.ylabel("The ratio of average return amount")#设置Y轴标签
plt.show()#显示图像

运行结果：
在这里插入图片描述
看来商业中的实际数据总是和课本上的完美数据不一样，看这零零散散的分布，线性关系很是勉强，但是大致还是有一个线性相关的样子的，那么就看看相关系数有多少吧。

相关系数R

rDf = examDf.corr()#查看数据间的相关系数
print(rDf)

运行结果：

         Call   Connect    Return

Call 1.000000 0.445870 0.441673
Connect 0.445870 1.000000 0.745338
Return 0.441673 0.745338 1.000000
Connect（接通量）和Return（回款量）的相关系数为0.745338，还不错。

相关系数是用以反映变量之间相关关系密切程度的统计指标，对于相关性强度来说，我们一般认为：

0~0.3 弱相关

0.3~0.6 中等程度相关

0.6~1 强相关

在数学中，相关系数的计算一般是这样的，给数学狂人看：

R(相关系数) = X和Y的协方差 / (X的标准差 * Y的标准差) == cov（X,Y）/ σX * σY （即person系数）

拆分训练集和测试集
Connect（接通量）和Return（回款量）属于强相关，可以进行线性回归训练，那么我们先来拆分训练集和测试集吧。

#拆分训练集和测试集（train_test_split是存在与sklearn中的函数）
X_train,X_test,Y_train,Y_test = train_test_split(examDf.Connect,examDf.Return,train_size=0.8)
#train为训练数据,test为测试数据,examDf为源数据,train_size 规定了训练数据的占比
 
print("自变量---源数据:",examDf.Connect.shape, "；  训练集:",X_train.shape, "；  测试集:",X_test.shape)
print("因变量---源数据:",examDf.Return.shape, "；  训练集:",Y_train.shape, "；  测试集:",Y_test.shape)
 
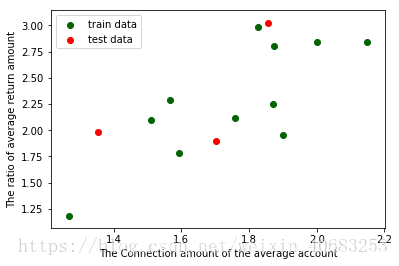
#散点图
plt.scatter(X_train, Y_train, color="darkgreen", label="train data")#训练集为深绿色点
plt.scatter(X_test, Y_test, color="red", label="test data")#测试集为红色点
 
#添加标签
plt.legend(loc=2)#图标位于左上角，即第2象限，类似的，1为右上角，3为左下角，4为右下角
plt.xlabel("The Connection amount of the average account")#添加 X 轴名称
plt.ylabel("The ratio of average return amount")#添加 Y 轴名称
plt.show()#显示散点图

运行结果：

自变量—源数据: (14,) ； 训练集: (11,) ； 测试集: (3,)
因变量—源数据: (14,) ； 训练集: (11,) ； 测试集: (3,)
在这里插入图片描述
回归模型训练

#调用线性规划包
model = LinearRegression()
 
#线性回归训练
model.fit(X_train,Y_train)#调用线性回归包
 
a  = model.intercept_#截距
b = model.coef_#回归系数
 
#训练数据的预测值
y_train_pred = model.predict(X_train)
#绘制最佳拟合线：标签用的是训练数据的预测值y_train_pred
plt.plot(X_train, y_train_pred, color='blue', linewidth=2, label="best line")
 
#测试数据散点图
plt.scatter(X_train, Y_train, color='darkgreen', label="train data")
plt.scatter(X_test, Y_test, color='red', label="test data")
 
#添加图标标签
plt.legend(loc=2)#图标位于左上角，即第2象限，类似的，1为右上角，3为左下角，4为右下角
plt.xlabel("The Connection amount of the average account")#添加 X 轴名称
plt.ylabel("The ratio of average return amount")#添加 Y 轴名称
plt.show()#显示图像
 
print("拟合参数:截距",a,",回归系数：",b)
print("最佳拟合线: Y = ",round(a,2),"+",round(b[0],2),"* X")#显示线性方程，并限制参数的小数位为两位

运行结果：
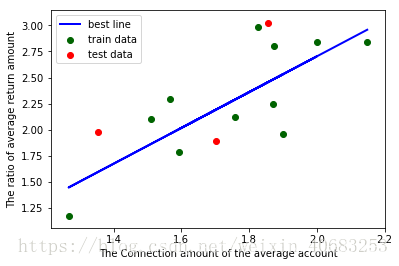
在这里插入图片描述
拟合参数:截距 -0.7291766860887745 ,回归系数： [1.71584366]
最佳拟合线: Y = -0.73 + 1.72 * X
补充一句，有博友说单变量线性回归上面的这段代码中，加一个reshape就能运行出来了，可能是版本不同，我没加也能运行出来，所以分享在下面给大家参考一下，如果有和博友一样的情况，可以试试增加下面一段代码（谢谢博友 dsy23 的分享）：

#调用线性规划包
model = LinearRegression()
 
 
#在这里加一段
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
 
 
 
#线性回归训练
model.fit(X_train,Y_train)#调用线性回归包
 
a  = model.intercept_#截距
b = model.coef_#回归系数

多变量线性回归
在单变量线性回归中，我们将每一步都讲解的极其详细，所以在多变量线性回归中，我们不会重复讲那些简单的部分了，但是为了防止python小白迷失自己，所以在这部分该有的代码还是会甩出来，该有的备注也都有，只不过不会一点一点分步骤来了。

上面我们提到多变量线性回归的模型为h(x)=theta0 + theta1* x 1 + theta2* x 2 + theta3* x 3，下面，我们还是使用单变量线性回归中的数据，单变量线性回归中，我们只用到了Connect（接通量）和Return（回款量），既然是多变量回归模型，那么我们就多加一个变量Call（拨打量）。

数据检验（判断是否可以做线性回归）

#-*- coding:utf-8 -*- 
 
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
 
#读取文件
datafile = u'E:\\pythondata\\dhdhdh.xlsx'#文件所在位置，u为防止路径中有中文名称，此处没有，可以省略
data = pd.read_excel(datafile)#datafile是excel文件，所以用read_excel,如果是csv文件则用read_csv
examDf = DataFrame(data)
 
#数据清洗,比如第一列有可能是日期，这样的话我们就只需要从第二列开始的数据，
#这个情况下，把下面中括号中的0改为1就好，要哪些列取哪些列
new_examDf = examDf.ix[:,0:]
 
#检验数据
print(new_examDf.describe())#数据描述，会显示最值，平均数等信息，可以简单判断数据中是否有异常值
print(new_examDf[new_examDf.isnull()==True].count())#检验缺失值，若输出为0，说明该列没有缺失值
 
#输出相关系数，判断是否值得做线性回归模型
print(new_examDf.corr())#0-0.3弱相关；0.3-0.6中相关；0.6-1强相关；
 
#通过seaborn添加一条最佳拟合直线和95%的置信带，直观判断相关关系
sns.pairplot(data, x_vars=['Call','Connect'], y_vars='Return', size=7, aspect=0.8, kind='reg')  
plt.show()

运行结果：

        Call    Connect     Return

count 99.000000 99.000000 99.000000
mean 3.153649 1.967779 2.591121
std 1.027607 0.470364 0.790172
min 1.280100 1.014208 0.941292
25% 2.373528 1.596610 2.044147
50% 3.040000 1.913472 2.476091
75% 3.835980 2.253994 3.035603
max 5.851181 3.234977 5.160840
Call 0
Connect 0
Return 0
dtype: int64
Call Connect Return
Call 1.000000 0.837052 0.744792
Connect 0.837052 1.000000 0.844640
Return 0.744792 0.844640 1.000000
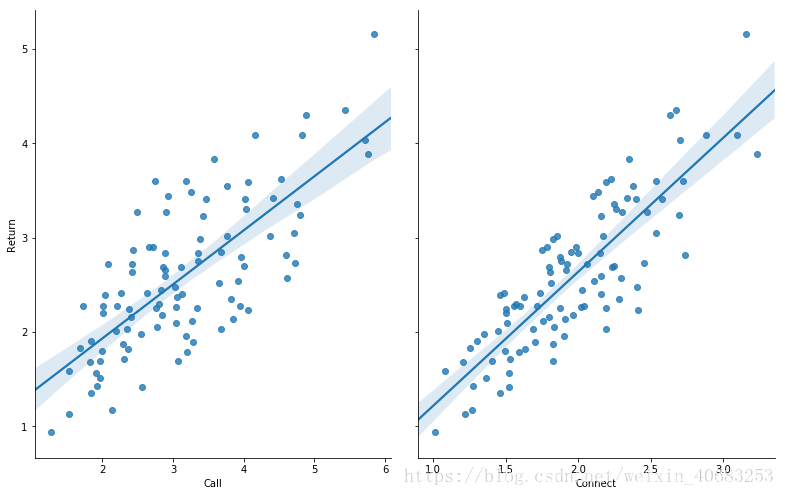
在这里插入图片描述
判断是否可以做线性回归：

异常值：通过最值或者平均数或者中位数等判断，或者直接通过查看是否有游离在大部队之外的点来判断是否有异常值；
空值：这个没办法，你必须看运行结果的10-12行是否等于0，是0则无空值，如果不是0，就要看看是删掉空值呢？还是用其他值代替呢？不同情况不同对待；
相关性：要么通过相关系数的大小判断，要么看散点图中的最佳拟合直线和95%的置信带，直观判断相关关系；

训练线性回归模型

#拆分训练集和测试集
X_train,X_test,Y_train,Y_test = train_test_split(new_examDf.ix[:,:2],new_examDf.Return,train_size=0.8)
#new_examDf.ix[:,:2]取了数据中的前两列为自变量，此处与单变量的不同
 
print("自变量---源数据:",new_examDf.ix[:,:2].shape, "；  训练集:",X_train.shape, "；  测试集:",X_test.shape)
print("因变量---源数据:",examDf.Return.shape, "；  训练集:",Y_train.shape, "；  测试集:",Y_test.shape)
 
#调用线性规划包
model = LinearRegression()
 
model.fit(X_train,Y_train)#线性回归训练
 
a  = model.intercept_#截距
b = model.coef_#回归系数
print("拟合参数:截距",a,",回归系数：",b)
 
#显示线性方程，并限制参数的小数位为两位
print("最佳拟合线: Y = ",round(a,2),"+",round(b[0],2),"* X1 + ",round(b[1],2),"* X2")
 
Y_pred = model.predict(X_test)#对测试集数据，用predict函数预测
 
plt.plot(range(len(Y_pred)),Y_pred,'red', linewidth=2.5,label="predict data")
plt.plot(range(len(Y_test)),Y_test,'green',label="test data")
plt.legend(loc=2)
plt.show()#显示预测值与测试值曲线

运行结果：

自变量—源数据: (99, 2) ； 训练集: (79, 2) ； 测试集: (20, 2)
因变量—源数据: (99,) ； 训练集: (79,) ； 测试集: (20,)
拟合参数:截距 -0.006540954521370601 ,回归系数： [0.08624344 1.19029593]
最佳拟合线: Y = -0.01 + 0.09 * X1 + 1.19 * X2
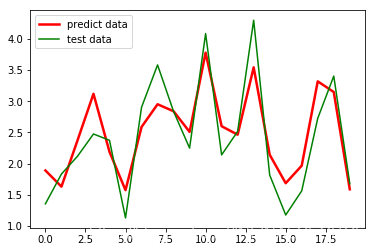
在这里插入图片描述
效果勉强满意，毕竟才用了80个数训练的模型，要求高的话多用一些数据就好。

原文链接：https://blog.youkuaiyun.com/weixin_40683253/article/details/81109129

Python实现多元线性回归(Multiple Linear Regression)
优快云 精品推荐
03-27 4014
多元线性回归是一种用于建立多个自变量与因变量之间关系的统计学方法。在多元线性回归中，我们可以通过多个自变量来预测一个因变量的值。每个自变量对因变量的影响可以用回归系数来表示。
多元线性回归（Multiple Linear Regression）吴恩达老师课程笔记
qq_71173859的博客
06-10 1123
​ 在线性回归的原始版本中，只有一个特征x，也就是房屋的大小，我们依据x来预测y，也就是房屋的价格，该模型是fwb​xwxb​ 但是现在我们在预测房屋价格的时候，并不仅仅考虑房屋的大小，还要考虑卧室的数量，楼层的数量和房屋的使用年限，那会怎么样呢？​ 由于多了几个特征，之前的模型也要做进一步的修改fwb​xw1​x1​w2​x2​w3​x3​w4​x4​b。
机器学习-多元线性回归
weixin_44208433的博客
02-10 1052
多元线性回归 多元线性回归尝试通过一个线性方程来适配观测数据，这个线性方程是在两个以上（包括两个）的特征和响应之间构建的一个关系。多元线性回归的实现步骤和简单线性回归很相似，在评价部分有所不同。你可以用它来找出在预测结果上哪个因素影响力最大，以及不同变量是如何相互关联的。 前提：想要有一个成功的回归分析，确认这些嘉定很重要 1、线性：自变量和因变量的关系应该是线性的（也即特征值和预测值是线性相关...
机器学习（多元线性回归）
zoinsung_lee的博客
11-14 5532
1.与简单线性回归的区别 多个自变量（x）2.多元回归模型 y= β0+ β1*x1+ β2*x2+……..+ βp*xp+e 其中 β1， β2，… βp, β0是参数 e是误差值3.多元回归方程 E（y）= β0+ β1*x1+ β2*x2+……..+ βp*xp4.估计多元回归方程 y=b0+b1*x1+b2*x2+……+bp*xp代码实现： 自变量只为数值型：数据文件： #
机器学习：多元线性回归
10-08
1. 样本大小为47，自变量为房间的面积和卧室个数，因变量为房间的价格。 2. 用梯度下降方法实现多变量的回归问题。 3. 选择learning rate α，范围是0.001≤α≤10。将通过初始选择、运行梯度下降和观察代价函数相应地调整学习速率。在该初始学习率下运行50次梯度下降迭代，并存储在相应的vector J中，并将所有的J画在同一副图中进行比较。做出与实验指导书中相同的图，选择最优α值，并回答以下问题： （1） 观察α值变化对cost function的影响，当α值过大或过小时会发生什么？ （2） 通过线性回归预测当面积为1650和卧室数为3个时，对应的房子价格。 4. 使用normal equation方法，使用这个公式不需要任何特征缩放，在一个计算中你会得到一个精确的解决方案：梯度下降之前没有“循环直到收敛”。计算出θ值以及预测当面积为1650和卧室数为3个时，对应的房子价格，并与上述值比较。
【机器学习】多元线性回归
Mount256的博客
02-18 2382
其中，第一项称为均方误差（mean squared error），第二项称为正则化项（regularization term），使。的标准差（Standard Deviation，std），即。将原有特征值通过组合或转化等方式变成新特征值。的平均值（mean），即。
精选资源
Multiple-Linear-Regression-ML:多元线性回归机器学习
04-01
本项目名为"Multiple-Linear-Regression-ML"，显然主要关注的是如何使用Python编程语言实现多元线性回归模型。 Python作为一种强大的数据科学工具，拥有丰富的库支持机器学习任务，如NumPy用于数值计算，Pandas用于...
精选资源
机器学习之多变量线性回归(Linear Regression with Multiple Variables).md
01-12
机器学习： 3.1 矩阵和向量 3.2 加法和标量乘法 3.3 矩阵向量乘法 3.4 矩阵乘法 3.5 矩阵乘法的性质 3.6 逆、转置
精选资源
Boston-Model-Housing-prices-Multiple-Regression:使用多元回归模型从sklearn.datasets.load_boston预测房价
03-16
2. **多元线性回归（Multiple Linear Regression）**：这是一种统计方法，用于研究多个自变量与一个连续因变量之间的关系。在这个案例中，我们的目标是通过13个特征来预测房价（MEDV）。多元线性回归模型假设自变量...
【机器学习】机器学习之多元线性回归
热门推荐
YangMax1的博客
10-21 1万+
这里写目录标题一、多元线性回归基础理论二、案例分析三、数据预处理1.错误数据清洗2.非数值型数据转换四、使用Excel实现回归1.回归实现2.回归分析五、使用Sklearn库实现回归六、总结七、参考 一、多元线性回归基础理论   在研究现实问题时，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归。当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元性回归。线性回归的数学模型为： f(xi)=ωTxi+bf(\pmb x_i)=\
机器学习之多元线性回归
sz1125218970的博客
12-09 1090
ml笔记
机器学习——多元线性回归
qq1851417332的博客
08-10 2319
线性回归是统计学和机器学习中最基础、最广泛使用的预测方法之一，用于建立自变量（特征）与因变量（目标）之间的线性关系模型。
ml-regression-simple-linear 能处理多元线性回归系数么
最新发布
10-23
<think>首先，用户的问题是关于机器学习中的线性回归模型。用户问：“ml-regression-simple-linear是否能处理多元线性回归系数？” 用户指的是一个特定的模型或库，叫做“ml-regression-simple-linear”，但从上下文看，这可能是一个误解或打字错误。 回顾引用： - 引用[1]：讨论多元线性回归（multivariable linear regression）。 - 引用[2]：提到简单线性回归（Simple Linear Regression）和性能指标如R-squared。 - 引用[3]：也讨论多元线性回归，包括特征选择和多项式回归。 用户的问题中提到了“ml-regression-simple-linear”，这听起来像是来自scikit-learn库中的一个类。在scikit-learn中，线性回归模型是通过`sklearn.linear_model.LinearRegression`实现的，这个模型可以处理多元线性回归。 具体来说： - 简单线性回归（simple linear regression）处理一个自变量（特征）和一个因变量。 - 多元线性回归（multiple linear regression）处理多个自变量和一个因变量。 在scikit-learn中，`LinearRegression`类可以处理多个特征，因此它支持多元线性回归。用户提到的“ml-regression-simple-linear”可能是一个误解；或许用户指的是`sklearn.linear_model.LinearRegression`，或者是一个特定的函数。 从引用[2]中，我们看到代码使用了`from sklearn.metrics import r2_score`和`regressor.predict(X_test)`，这表明使用了scikit-learn的回归模型。 所以，关键点是：scikit-learn的LinearRegression模型可以处理多元线性回归系数。 现在，基于系统指令： - 我必须使用中文回答。 - 行内数学表达式用$...$，例如 $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon$。 - 独立公式用$$...$$，单独成段。 - LaTeX语法正确。 - 生成相关问题。 - 引用末尾添加引用标识。 - 回答结构清晰，逐步解决问题。 组织回答： 1. **澄清问题**：解释“ml-regression-simple-linear”可能指的是scikit-learn的LinearRegression模型。 2. **直接回答**：是的，它可以处理多元线性回归系数。 3. **解释原因**：描述多元线性回归模型和LinearRegression的实现。 4. **提供数学背景**：使用数学表达式展示多元线性回归公式。 5. **引用支持**：基于提供的引用，引用[1]和[3]讨论了多元线性回归。 6. **生成相关问题**：在末尾添加相关问题。 回答结构： - 开头：直接回答问题。 - 主体：解释多元线性回归模型，使用数学公式。 - 结尾：确认模型能力。 - 然后：添加相关问题。 确保LaTeX正确： - 行内：$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2$ - 独立： $$ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon $$ 生成相关问题：基于主题，如： - 多元线性回归的假设是什么？ - 如何解释多元线性回归的系数？ - scikit-learn中如何使用LinearRegression模型？ 引用末尾添加标识：[^1], [^2], [^3] 基于引用内容。 最后，确认回答可靠：基于标准机器学习知识。 </think>基于您的查询和提供的引用，我将逐步解释“ml-regression-simple-linear”是否能处理多元线性回归系数。首先澄清关键概念： - **简单线性回归（Simple Linear Regression）**：处理一个自变量（特征）和一个因变量，模型形式为 $y = \beta_0 + \beta_1 x$，其中 $\beta_0$ 是截距，$\beta_1$ 是斜率系数。 - **多元线性回归（Multivariable Linear Regression）**：处理多个自变量（特征）和一个因变量，模型形式为： $$ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n + \epsilon $$ 其中 $\beta_0, \beta_1, \ldots, \beta_n$ 是回归系数，$\epsilon$ 是误差项[^1][^3]。 ### 回答您的核心问题 **是的，“ml-regression-simple-linear”通常可以处理多元线性回归系数。** 具体说明如下： 1. **模型名称澄清**： - “ml-regression-simple-linear”听起来像是指 scikit-learn（Python 机器学习库）中的 `LinearRegression` 类（通常在代码中导入为 `from sklearn.linear_model import LinearRegression`）。 - 虽然名称包含 “simple”，但 scikit-learn 的实现支持多元回归。在训练时，如果输入特征矩阵 $X$ 有多个列（即多个特征），模型会自动估计多元回归系数 $\beta_0, \beta_1, \ldots, \beta_n$[^2][^3]。 2. **技术细节**： - scikit-learn 的 `LinearRegression` 使用梯度下降或正规方程（normal equation）求解多元系数，目标是最小化代价函数（cost function）： $$ J(\beta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\beta(x^{(i)}) - y^{(i)})^2 $$ 其中 $m$ 是样本数，$h_\beta(x)$ 是假设函数，对应多元模型[^1]。 - 在代码中（如引用[2]所示），当使用 `regressor.predict(X_test)` 时，`X_test` 可以包含多个特征列，模型会输出基于多元系数的预测值。 3. **验证示例**： - 假设您有数据集包含两个特征 $x_1$ 和 $x_2$，模型训练后会返回系数 $\beta_0$（截距）、$\beta_1$（对应 $x_1$）、$\beta_2$（对应 $x_2$）。 - 在 scikit-learn 中，系数可通过 `model.coef_` 属性获取，例如： ```python from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X_train, y_train) # X_train 有多个特征列 print(model.coef_) # 输出多元系数数组，例如 [β1, β2, ...] ``` 这证明它能处理多元场景[^2][^3]。 4. **限制与注意**： - 如果模型名称严格指代“一元线性回归”（只一个特征），则不能处理多元系数。但在实践中，库的实现通常是通用的。 - 多元回归需满足假设（如线性、独立同分布误差），否则系数估计可能不准确[^1][^3]。 总之，基于 scikit-learn 的标准实现，“ml-regression-simple-linear” 能有效处理多元线性回归系数。更多细节可参考官方文档或引用资源[^1][^2][^3]。
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值