机器学习-逻辑（logistic）回归

来自吴恩达老师的机器学习课程作业，参考ladykaka007的讲解视频，根据西瓜书上的公式进行了修改。

任务：

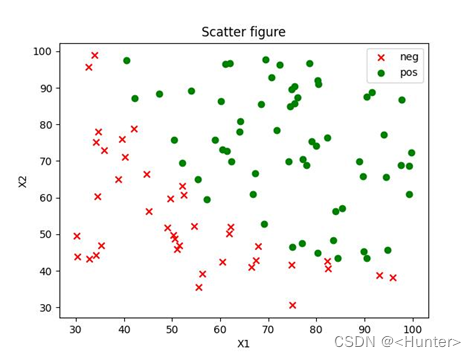
根据两个数据维度分类（数据可视化后如下图，具体数据见文件末尾），判断是正例还是反例。

一、数据预处理

首先读入数据，在X中插入一行X0方便后续的矩阵运算。然后绘制出数据的散点图（如图1），分正例和反例，发现数据线性可分，可以使用逻辑回归的方法进行分类。

def read_data(path):#读入数据并命名
    data=pd.read_csv('data_nonreg.csv',header=None)
    label=['X'+str(i+1) for i in range(data.shape[1]-1)]
    label.append('Y')
    data.columns=label
    data['X0']=1
    label=['X'+str(i) for i in range(data.shape[1]-1)]
    m=len(data)
    X=np.array(data[label].values)
    y=np.array(data['Y'].values.reshape(m,1))
    return data,X,y

#读入数据
data,X,y=read_data('data_nonreg.csv')
#画是散点图，数据可以做一个超平面，使用逻辑回归
Ndata=data[data['Y']==0]#negative data
Pdata=data[data['Y']==1]#pos.. data
#绘图P->go,N->ro
plt.figure('oral_picture')
plt.scatter(Ndata['X1'],Ndata['X2'],c='r',marker='x',label='neg')
plt.scatter(Pdata['X1'],Pdata['X2'],c='g',marker='o',label='pos')
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Scatter figure')
plt.legend()
plt.savefig('oralscatter.jpg')
plt.show()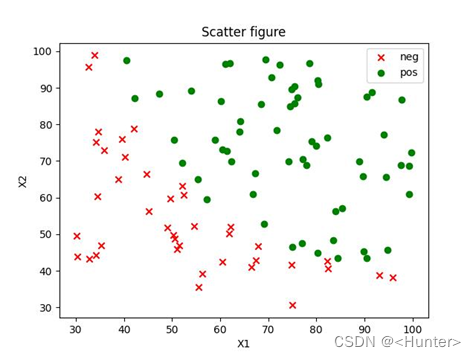

图1 原始数据散点图

 二、模型训练

根据西瓜书上的公式，进行训练，主要用到的有：

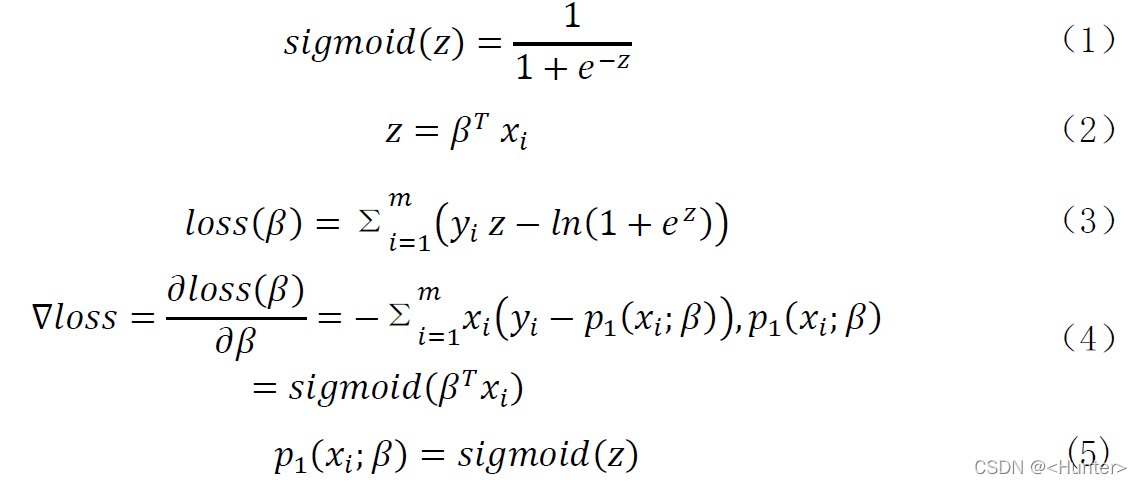
对于公式（4）结合矩阵乘法的运算特性，可以化简为（6）方便程序中的运算：

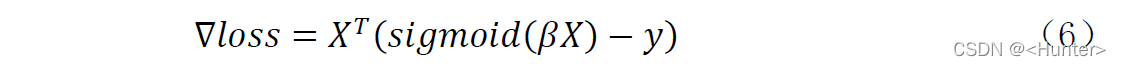
 主要要达到的目的是使得loss最大，即（7）。

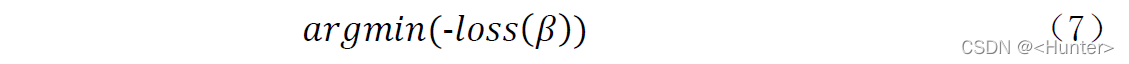
采用梯度下降策略，主要流程的伪代码为：

 

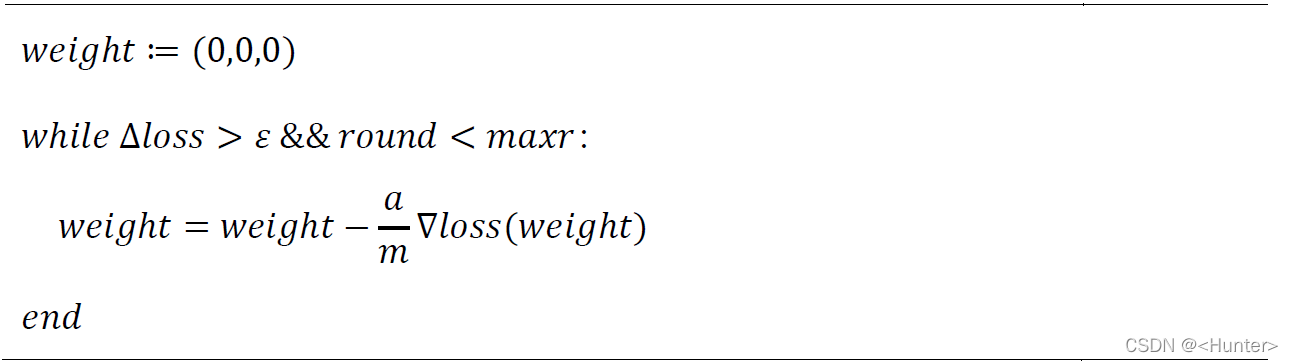
其中a为学习率,maxr为最大轮数限制，代码中采用0.001作为学习率进行训练，最终训练10824693后结束，训练的loss变化曲线如图2。 

对应的代码为：

def sigmoid(z):#激活函数
    return 1/(1+np.exp(-z))

def solloss(X,y,weights):#求解loss
    z=np.dot(X,weights)
    m=len(y)
    return (y*z-np.log(1+np.exp(z))).sum()/m#/m防止overflow

def solweights(X,y,a,maxr=10000000000000000,outlim=10000,weights=np.zeros([3,1])):
    '''
        maxr:迭代最大轮数
        outlim：输出限制
        weight:权重，默认(0,0,0)
    '''
    m=len(y)
    eci=0.00000000001
    loss=solloss(X,y,weights)
    preloss=1000000#inf
    r=0
    allloss=[]
    while(abs(preloss-loss)>eci and r<maxr):#两次loss差别不大时退出,收敛条件
        preloss=loss
        sigz=sigmoid(np.dot(X,weights))
        weights=weights-a/m*np.dot(X.transpose(),(sigz-y))#梯度下降
        loss=solloss(X,y,weights)
        r+=1
        allloss.append(loss)
        if(r%outlim==0):
            print('round:',r,',loss:',loss)
    print('----------FINAL:','round',r,',loss',loss,',weight[',[x[0] for x in weights],']----------')
    plt.figure('LOSS figure')
    plt.plot(allloss)
    plt.xlabel('round')
    plt.ylabel('loss')
    plt.title('LOSS figure')
    plt.savefig('loss.jpg')
    pl