点与坐标系
2D的情况:用两个坐标加旋转角表达
3D的情况:?
在描述3D的情况前,可以先描述一些基本概念:
坐标系、点、向量、向量的坐标
坐标系(参考系)任何运动都是相对的,需要一个参考系。只能说哪个东西在某个参考系下看起来是怎样的运动、它位于什么位置等等。参考系一般是由三个轴组成的迁移空间的一个基,基向量,正常情况下这三个基向量都是彼此正交的。有两种不同的定义方式,左手系和右手系,除大拇指外的四个指头从x转到y,大拇指的方向如果向上就是右手系,反之左手系,两种方式没有优劣之分,在这里我们采用右手系。
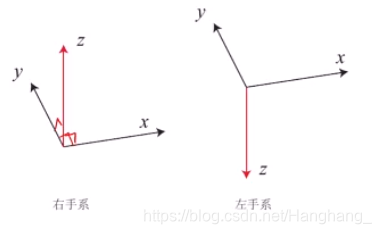
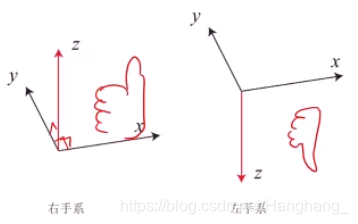
若要讨论运动,一般是在坐标系讨论的。而且往往会讨论到几个坐标系,有一些坐标系是固定的,一些坐标系是运动的,一般我们关心多少个物体就考虑多少个坐标系。
比如一个相机在世界当中运动,这时候建立两个坐标系。一个是世界坐标系,一个是相机坐标系。
我们要关心的是这两个坐标系之间的变换是怎么样子的。
例如:建立一个点P,这个点在两个坐标系的位置是不一样的,已知P在世界坐标轴的位置,如何去变换到相机坐标轴下的坐标?
如果是一个机器人的话,那这样会更加复杂,比如机器人本体需要建立一个坐标系,机械臂也需要建立一个坐标系,激光雷达也会有一个坐标系。如果知道每一个坐标系的位置坐标关系,就可以很方便地讨论某一个数据在一个坐标系下的运动情况,在另一个坐标系下的运动情况。
在世界坐标系中,由于坐标系由三个互相正交的向量基组成,向量P可以由三个基的线性组合所构成,且唯一。向量表示为: P = a 1 x + a 2 y + a 3 z = ( a 1 a 2 a 3 ) T ( x y z ) P=a_1x + a_2y + a_3z = \left(\begin{array}{ccc}{a_1} & {a_2} & {a_3} \\ \end{array}\right)^{T} \left(\begin{array}{ccc}{x} & {y} & {z} \\ \end{array}\right) P=a1x+a2y+a3z=(a1a2a3)T(xyz) 然后我们就可以讨论同样的一个P,它在另一个坐标系下是如何表示的,这几个坐标之间是如何 这是本节所要讨论的问题。
向量的运算可由坐标运算表达
加法和减法
其中两向量的加法和减法,可以使用平行四边形法则来表示。
内积 : 点乘
a ⋅ b = a T b = ∑ i = 1 3 a i b i = ∣ a ∥ b ∣ cos ⟨ a , b ⟩ \boldsymbol{a} \cdot \boldsymbol{b}=\boldsymbol{a}^{T} \boldsymbol{b}=\sum_{i=1}^{3} a_{i} b_{i}=|\boldsymbol{a} \| \boldsymbol{b}| \cos \langle\boldsymbol{a}, \boldsymbol{b}\rangle a⋅b=aTb=i=1∑3aibi=∣a∥b∣cos⟨a,b⟩
外积 : 叉乘
a × b = [ i j k a 1 a 2 a 3 b 1 b 2 b 3 ] = [ a 2 b 3 − a 3 b 2 a 3 b 1 − a 1 b 3 a 1 b 2 − a 2 b 1 ] = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] b ≜ a ∧ b \boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc}{i} & {j} & {k} \\ {a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}}\end{array}\right]=\left[\begin{array}{c}{a_{2} b_{3}-a_{3} b_{2}} \\ {a_{3} b_{1}-a_{1} b_{3}} \\ {a_{1} b_{2}-a_{2} b_{1}}\end{array}\right]=\left[\begin{array}{ccc}{0} & {-a_{3}} & {a_{2}} \\ {a_{3}} & {0} & {-a_{1}} \\ {-a_{2}} & {a_{1}} & {0}\end{array}\right] b \triangleq a^{\wedge} b a×b=⎣⎡ia1b1ja2b2ka3b3⎦⎤=⎣⎡a2b3−a3b2a3b1−a1b3a1b2−a2b1⎦⎤=⎣⎡0a3−a2−a30a1a2





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








