二维差分问题----个人学习总结(C++)

题目描述：

输入一个 n 行 m 列的整数矩阵，再输入 qq 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1)和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c 表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

二维差分思想：

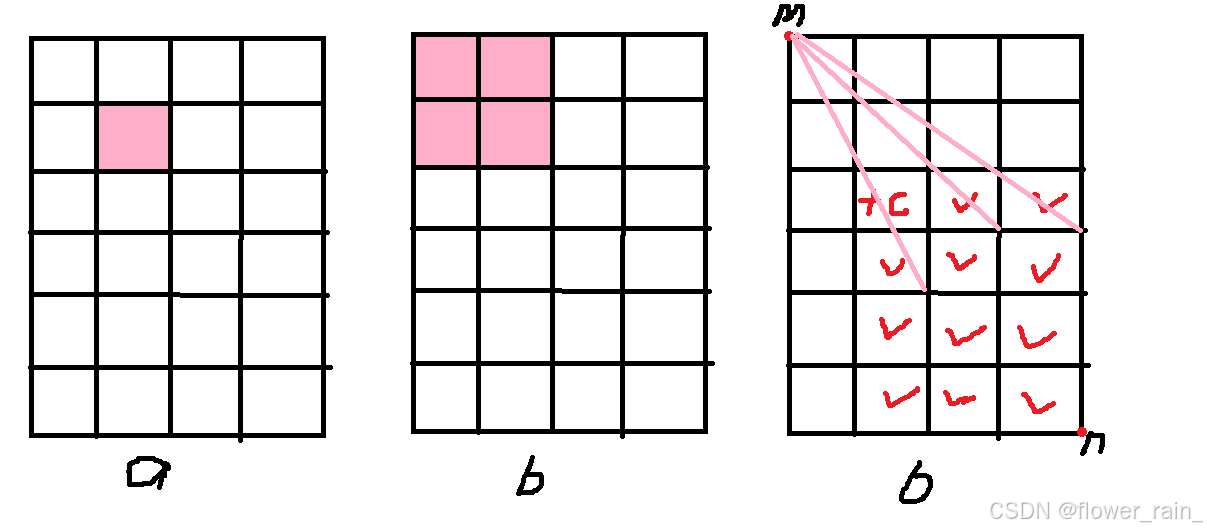
1.差分数组的含义。

我们把给定数组看为前缀和数组，类比二维前缀和的做法，构造一个差分数组b，使得 a [ i ] [ j ] 是 b [ i ] [ j ] 到左上角连线的矩阵中的所有数之和。如图上粉色方块所示。

2. 构造这样的差分数组 b 该如何利用。

我们看到上图第三个矩形，如果在所示位置加 c ，那么最后在求  b 数组的前缀和的时候，会让打对号的位置都加上 c ( 因为它们和左上角的连线的矩形中都会包含 +c 的那个数，可以先回忆一下二维前缀和怎么求，基本公式是s [ i ] [ j ] = s [ i - 1] [ j ] + s[ i ] [ j - 1] - s [ i - 1] [ j - 1] + a [ i ] [ j ] ) 理解了这个性质我们就可以很好地降低时间复杂度了。

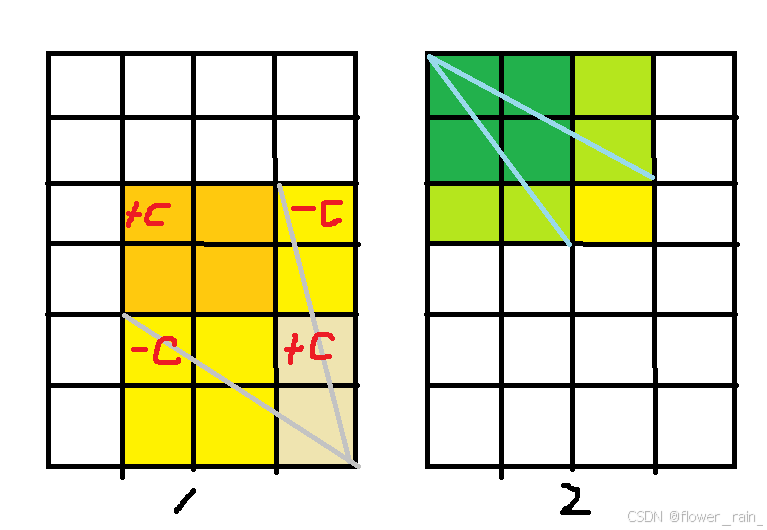
如图，我们想让橙色部分加上c，但是我们并不想让后面所有数都加，因此需要打几个补丁，图上标的很清楚，由于浅棕色的地方被减了两次，所有我们还要再加一次。据此，我们就可以编写一个insert函数，帮助我们插入

 

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

3. 如何根据已知数组 a ，构造出差分数组 b

这里我们需要类比前面插入 c 的方式，把 a 数组里面的数看成插入 c ，我们具体看代码分析一下

代码呈现：

#include <iostream>

using namespace std;

const int N = 1010;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    int n,m,q;
    scanf("%d %d %d",&n,&m,&q);
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            scanf("%d",&a[i][j]);
        }
    }
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            insert(i,j,i,j,a[i][j]);
        }
    }
    while(q--){
        int x1,y1,x2,y2,c;
        scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            b[i][j] += b[i - 1][j] + b[i][j - 1] -b[i - 1][j - 1];
        }
    }
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            printf("%d ",b[i][j]);
        }
        printf("\n");
    }
}

 我们看到第二个双层for循环这里，这样的操作会让人一时之间以为是把 a 数组中的每一个数拷贝到了 b 数组，但其实不是这样的，这里只是 ( x1,y1 ) 与 ( x2,y2 )这两个点重合了而已，底层逻辑是不变的。这里我自己输入输出了一下，当给定这样的矩阵：

1 2 2 1
3 2 2 1
1 1 1 1

最后 b 数组会是这样：

1 1 0 -1 
2 -2 0 0 
-2 1 0 1 

可以加一下发现是满足我们之前规定的性质的，还是挺神奇的。