二维前缀和_子矩阵的和问题————个人学习总结(C++)

题目描述：

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q行，每行包含四个整数 x1,y1,x2,y2表示一组询问。

输出格式

共 q行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000
1≤q≤200000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤矩阵内元素的值≤1000

思路简析：

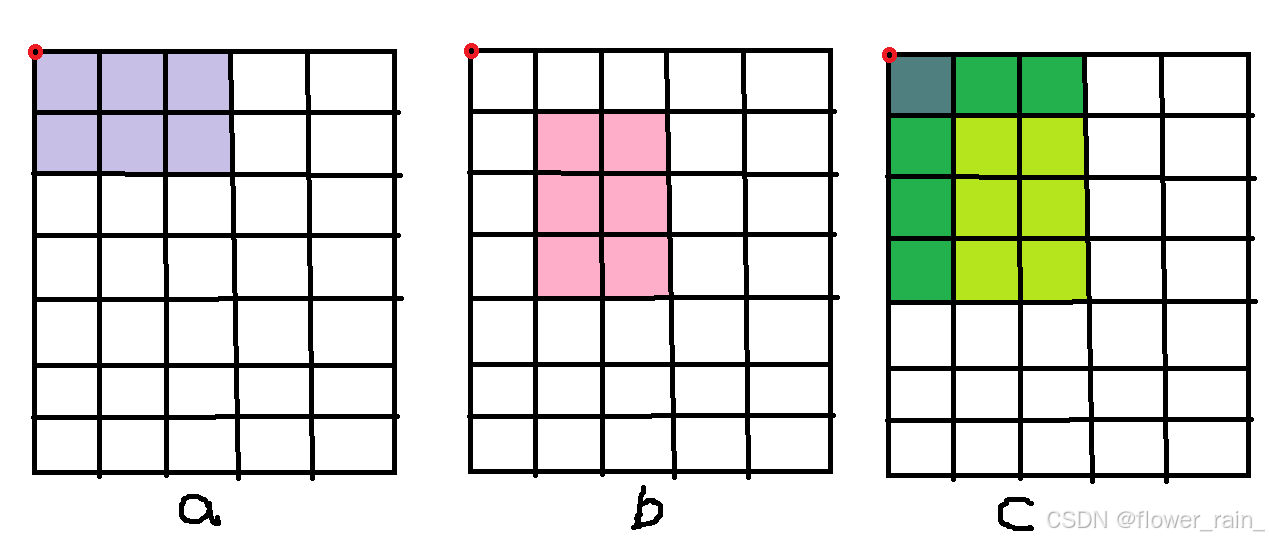
1.前缀和数组如何规定。首先前缀和一般都是从 1 开始计数，二维也不例外，已知第 i 行第 j 列，我们规定前缀和数组 s [ i ] [ j ] 表示其到原点所作对角线的矩形中所有小方框的和，如图a.

2.如何从题目中的数组过渡为前缀和数组。首先我们是从左到右一行一行处理的，当只处理一行的时候其实是一位的前缀和数组，但关键是到第二行如何处理。可以以图a为例求这个浅紫的方块。分析归纳后，基于前面的情况，基本公式为 s [ i ] [ j ] = s [ i - 1] [ j ] + s[ i ] [ j - 1] - s [ i - 1] [ j - 1] + a [ i ] [ j ]。因为是从1开始计数的，第0行和第0列的数都是0，所以这