二分算法模板解决数的范围问题----个人学习总结(C++)

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 482 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #学习 #c++

整数二分模板引入：

1.首先要明白二分与单调性的关系

有单调性一定可以二分，但是能二分的不一定必须有单调性，二分的本质是找到边界，当这个数可以分为两个性质并且每个性质都统一分布在左右两边时，我们就可以找到这个边界点。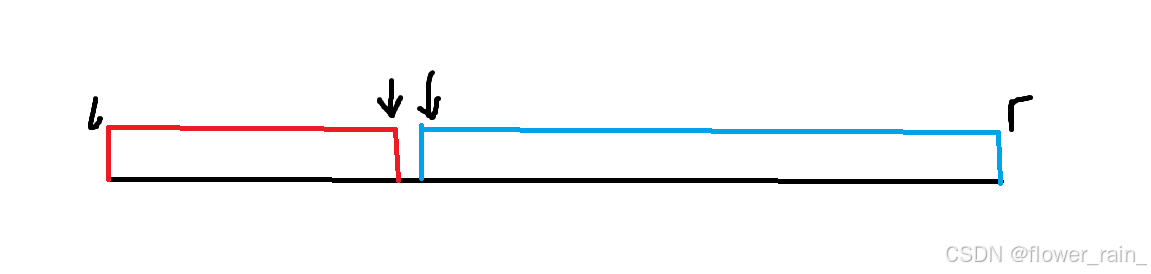

我们将数组大致想象成这样一个图，分为符合红色性质和符合蓝色性质，注意这并不是数轴，因此红蓝中间的空隙里并不存在整数。二分重要的是更新方式，我们先设一个mid.

2.求左半区的右边界点

当满足 l < r 的条件时我们进行如下操作，判断处于mid位置的数是否符合左半区的性质，如果符合说明它在红色区域且有可能位于边界点，那么我们就更新区间为 [ mid , r ]，否则便处于蓝色区域，那么我们就更新区间为 [ l , mid -1 ]。这里需要注意mid的求取，如果 l 和 r 仅相差 1 ，令mid = ( l + r ) / 2 时由于整型数据除法在计算机上是下取整，这里就相当于 mid = l ，带入第一种更新区间的方式就相当于没更新，会进入死循环，因此在这种情况下需要令 mid = (l + r + 1) / 2 噢。后面的蓝色边界点则不需要。

经过分析于是可以写出代码：

//性质在右半区不符合，而左半区符合，并找到符合性质的左半区的右边界点，像upper_bound
int bsearch_1(int l,int r)
{
    while(l<r){
        int mid = l + r + 1 >> 1;
        if(check(mid))
            l = mid;
        else
            r = mid - 1;
    }
    return l;
}

3.求右半区的左边界点

当满足 l < r 的条件时我们进行如下操作，判断处于mid位置的数是否符合右半区的性质，如果符合说明它在蓝色区域且有可能位于边界点，那么我们就更新区间为 [ l , mid ]，否则便处于红色区域，那么我们就更新区间为 [ mid + 1 , r ]。这里我们 mid 正常取 ( l + r ) / 2，因为不会出现更新后区间不变的情况，也就不会出现死循环。

经过分析于是可以写出代码：

//性质在右半区符合，而左半区不符合的，并找到符合性质的右半区的左边界点,像lower_bound
int bsearch_2(int l,int r)
{
    while(l<r){
        int mid = l + r >> 1;
        if(check(mid))
            r = mid;
        else
            l = mid + 1;
    }
    return l;
}

这里 mid 的设置有个巧记法，当你分析过判断为 true 时更新的是 l = mid ，就需要+1，类似于数学的左加右减，只不过去掉了减。

acwing789.数的范围问题解决：

1.代码呈现：

#include <iostream>

using namespace std;

const int N = 1e5+10;
int n,m;
int q[N];

int main()
{
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)
        scanf("%d",&q[i]);
    while(m--){
        int k;
        scanf("%d",&k);
        int l=0,r=n-1;
        while(l<r){
                int mid = l + r >> 1;
                if(q[mid]>=k)
                    r = mid;
                else
                    l = mid + 1;
            }
        if(q[l] != k)
            printf("-1 -1\n");
        else{
            printf("%d ",l);
            int l = 0,r = n-1;
            while(l<r){
            int mid = l + r + 1 >> 1;
            if(q[mid]<=k)
                l = mid;
            else
                r = mid - 1;
        }
            printf("%d\n",l);
        }
    }
    return 0;
}

如果理解透彻前面的二分算法，这道题的代码也不需要解释很多了，直接套模板就好了