【洛谷】P3387 【模板】缩点（Kosaraju 算法）

【洛谷】P3387 【模板】缩点（Kosaraju 算法）

---

洛谷专栏：模板，图论
洛谷模板：P3387 缩点
算法竞赛：图论，有向图的连通性问题
缩点算法：Kosaraju 算法
题目链接：洛谷 P3387

题目描述：
给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

---

缩点（Contraction of Strongly Connected Components）

是图论中对有向图进行简化的重要操作，其核心是将图中的强连通分量（SCC）合并为单个节点。

强连通分量（Strongly Connected Component, SCC）

在有向图中，如果两个顶点 $v$ 和 $u$ 之间有一条从 $v$ 到 $u$ 的有向路径，同时也有一条从 $u$ 到 $v$ 的有向路径，即两个顶点 $v$ 和 $u$ 之间存在双向路径，则称这两个顶点强连通，这些强连通的顶点之间构成强连通分量。有向图的极大强连通子图称为强连通分量。

本题做法是将一张有向图的强连通分量缩成一个点，这个点的点权为原来环上点的点权之和。

强连通分量和有向图相关基础知识可见 OI-WiKi。

缩点大致过程如下图。

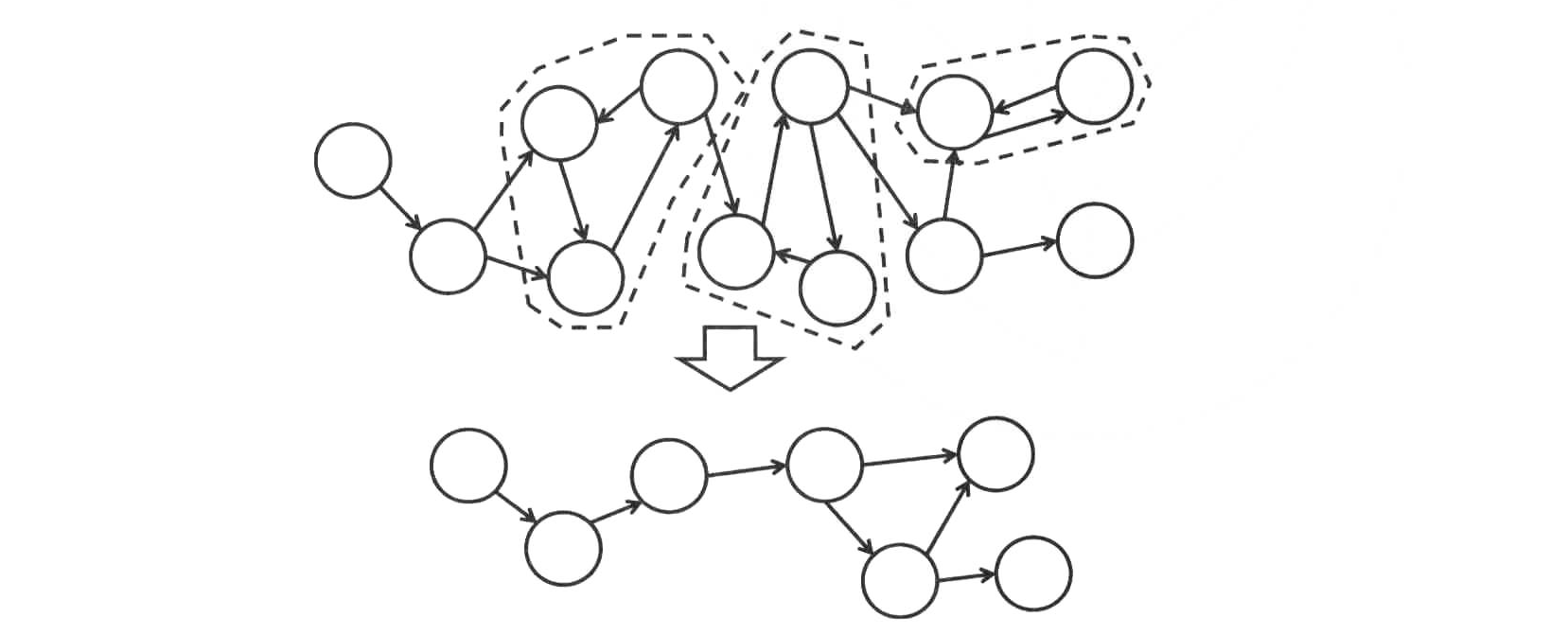
缩点步骤

1. 使用动态数组正反存图。
2. 正向 dfs 遍历图并存到存点数组里（图不一定联通；dfs 递归得到的数组顺序是从后往前）
3. 倒序 dfs 遍历存点数组，$ccnum $ 计组数（单点算一组，一个环算一组），$c_i=ccnum$ 表示编号为 $i$ 的点属于 $ccnum $ 组，$w_{ccnum}=w_{ccnum}+va{l}_i$ 将每组中的点求和，其中 $va{l}_i$ 表示点 $i$ 的点权，$w_{ccnum}$ 表示 $ccnum$ 组的组权。
4. 创建新图：循环遍历每个点的边，如果 $c_i\ne c_j$ 就存下这条点 $j$ 到点 $i$ 的有向边，其中 $i,j$ 为原图一条从点 $j$ 到点 $i$ 的有向边的两个顶点，$c$