内容来源:
崔希璋, 於宗俦, 陶本藻,等. 广义测量平差(新版)[M]. 武汉测绘科技大学出版社, 2001.
贴在这里以备不时之需,自己抄一边,也就理解个七七八八了😜
一、引子
为了说明动态系统的数学模型,我们首先举一个例子。卫星在空间飞行,在地球各地的卫星观测站对卫星的瞬时位置——角位置偏差进行观测,可以通过这些观测值来求定和预报卫星飞行轨道的偏差。由于卫星在飞行过程中受大气阻力的影响,要产生阻力加速度,其主要影响是改变卫星沿轨道切线方向的运动,使卫星轨道产生偏差,而不能按标称轨道运行。



二、数学模型
1、符号含义

2、连续线性系统
上述连续线性系统的状态方程是线性微分方程(为什么说是微分方程呢?过去平差求的不是一个参数向量吗,它应该是个值啊。这里是动态的系统,所要求的参数向量是随时间变化的,所以它可以看成是时间的函数,我们要求的状态向量就是一个关于时间的函数,所以这是一个微分方程!),它的通解等于它所对应的齐次方程的通解和非齐次方程的特解之和。为此,先求齐次状态方程



3、离散线性系统
如果仅在确定的瞬间来研究系统的性能,把这样的系统叫做离散时间系统. 一般来说,它包括两种情况:
- (1)系统本身就是一个离散的系统,对于这种系统,只能在离散的瞬间来研究系统的状态,而在这些时刻之间,系统的状态是没有意义的.
- (2)本身是连续的系统,但为了研究方便,仅在离散时间内研究其性能.
一个离散线性系统,通常是用一个具有随机初始状态,并带有动态噪声的线性差分方程和离散观测方程来描述。对于上述第二种情况,可以由相应的连续线性系统的状态方程和观测方程离散化得到。

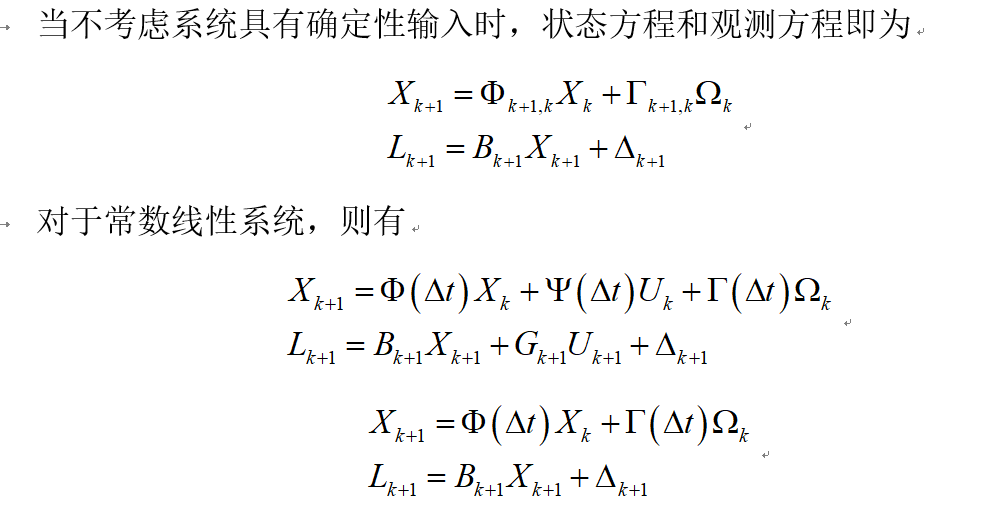

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










