[kuanbin带我飞]简单搜索

最新推荐文章于 2025-08-10 21:28:09 发布

原创最新推荐文章于 2025-08-10 21:28:09 发布 · 3.7k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#[kuanbin带我飞] #简单搜索 #算法 #POJ

算法题目练习专栏收录该内容

9 篇文章

订阅专栏

本文解析了三道简单搜索题目：FindTheMultiple、CatchThatCow和Fliptile，介绍了使用队列实现的算法思路，包括如何寻找能整除特定数字且仅由0和1组成的数，如何在二维平面上最少步骤捕获奶牛，以及如何翻转瓷砖以达到统一颜色的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

今天做了三道简单搜索的题目

Find The Multiple POJ - 1426

在这里插入图片描述
这道题看上去很唬人，我在集训总结赛的时候看到了这题，但那会被唬住了，也没看懂题目的意思，所以那会就没做，后面也没有做(黑脸)。
这道题的意思是给你一个200以内的数，让你找出可以整除这个数，而且数字只有0和1的数，这道题我们就用队列来做就好了。
先将1压入栈，然后不断地将它的10倍和10倍加1压入栈，因为题目要求是只有0和1，所以我们可以通过这个方法实现，然后不断出栈，直到找到可以整除它的数。

#include<iostream>
#include<cstdio>
#include<iostream>
#include<queue>
# define LOCAL
using namespace std;
typedef long long ll;
void bfs(int n){
	queue<ll> q;
	q.push(1);
	while(!q.empty()){
		ll temp = q.front();
		q.pop();
		if(temp%n == 0){
			cout << temp << endl;
			return;
		}
		q.push(temp*10);
		q.push(temp*10+1);
	} 
}
int main(){
std::ios::sync_with_stdio(false);
#ifdef LOCAL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
#endif
	int n;
	while(cin >> n && n){
		bfs(n);
	}
	return 0;
}

Catch That Cow POJ - 3278

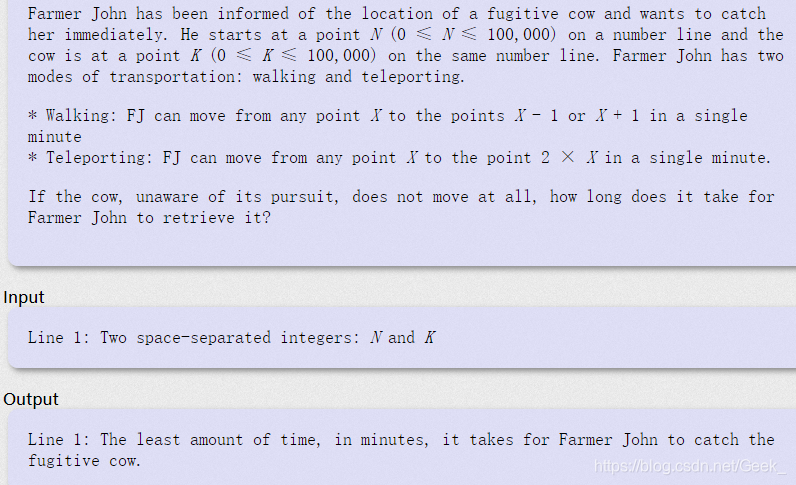
在这里插入图片描述
这道题是讲抓奶牛的故事，就是农民FJ每一次可以前进或者退后一步，或者直接跳当前位置的两倍，一开始我想用dfs来解决，但最后没有实现，这里就留一个疑问吧，或许以后就看到就知道怎么解决了。
所以这里我换了另一种方法，也是和上面那题一样，利用队列实现。这里代码相对详细一些，思路也和上面的类似，所以就略讲了，在判断是否入栈的时候，我们将三种情况都进行判断，如果没有越界并且没有走过的话，我们就把它压入栈。再读入数据之后我们需要对答案进行特判，就是当农民在奶牛前面或者同一位置的时候，我们就只能往回走，所以也就不需要用到队列。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
const int maxn = 2e5;	//大一些，否则会runtime error 
const int inf = 0x3f3f3f3f;
int n,k,ans=inf;
int d[maxn];//存储步数，下标是位置
int vis[maxn];//判断是否走过
/*void dfs(int cur,int step){
	int temp = cur;
	vis[temp] = 1;
	if(temp<0 || temp>k+n)
		return;
	else if(temp == k){
		if(step < ans)
			ans = step-1;
		return;
	}
	if(!vis[2*temp])
		dfs(2*temp,step+1);
	if(!vis[temp-1])
		dfs(temp-1,step+1);
	if(!vis[temp+1])
		dfs(temp+1,step+1);
}*///BUG

int bfs(){
	queue<int> q;
	q.push(n);
	vis[n] = 1;
	d[n] = 0;
	while(!q.empty()){
		int temp = q.front();
		q.pop();
		if(temp == k)
			break;
		int nx;
		for(int i=0;i<3;i++){
			if(i==0)
				nx = temp - 1;
			else if(i==1)
				nx = temp + 1;
			else
				nx = temp * 2;
			if(nx<0 || nx>k+n)
				continue;
			if(!vis[nx]){
				q.push(nx);
				vis[nx] = 1;
				d[nx] = d[temp] + 1;
			}
		}
	}
	return d[k];
}

int main(){
	std::ios::sync_with_stdio(false);
	while(cin >> n >> k){
		memset(vis,0,sizeof(vis));
		int ans;
		if(n < k)
			ans = bfs();
		else
			ans = n - k;
	//	dfs(n,0);
		cout << ans << endl;
	}
	return 0;
}

Fliptile POJ - 3279

在这里插入图片描述
这道题做的时候没有看懂，后来看了别人的题解才知道是咋回事，题目大概意思是说有黑白两面的瓷片，给定特定的瓷片摆放，然后需要翻转瓷片使得最后全部都是白色在上，其中翻转的时候，和它同边的也是同样被翻转。其中1表示黑色在上，0表示白色在上
这道题我们就用三个数组，一个存入初始数据，一个递归不断改变的数组，还有一个是答案数组，因为题目要求需要是最小的翻转次数，所以我们需要维护答案数据。我们从第一行开始不断地选择是否翻转瓷片，最后判断最后一行是否全部为0，如果是的话，就说明这个方案最后可以实现全部白色面在上，此时就判断是否要更新答案数据。
在dfs函数中，我们先通过判断当前的翻转数是否大于最小方案数，如果是的话，就没有必要往下走，算是一个剪枝操作。然后再通过判断最后一行是否符合条件，再判断是否要更新答案数据。对于每一行的瓷片决定是否要翻转，可以通过判断上一行对应瓷片是否翻转，还有相邻的瓷片是否为黑色来确定。如果满足条件，则翻转当前瓷片，并使翻转次数+1。我们通过调用getdfs函数来假设第一行是否翻转瓷片和不翻转瓷片，再调用dfs函数来对第一行每种情况进行搜索。

#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
# define LOCAL
using namespace std;
const int maxn = 17;
int mp[maxn][maxn];//存储输入的数据 
int tmp[maxn][maxn];//记录每一次改变的方案 
int ans[maxn][maxn];//最后输出的答案图 
int m,n;
int nmin = INF;//记录最小翻动方案 
inline int read(){
	char ch=getchar();int f=1,x=0;
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool judge(){
	for(int i=1;i<=n;i++){
		int t = tmp[m][i-1]+tmp[m][i]+tmp[m][i+1]+tmp[m-1][i];
		if((mp[m][i]+t)&1)
			return false;
	}
	return true;
}//判断最后一行是否全为0 
void dfs(int k,int cur){
	if(cur > nmin)//剪枝 
		return;
	if(k > m){
		if(judge() && nmin > cur){//判断是否需要更新 
			nmin = cur;
			memcpy(ans,tmp,sizeof(tmp));
		}
		return;
	}
	int t=0;
	for(int i=1;i<=n;i++){
		if((mp[k-1][i]+tmp[k-1][i]+tmp[k-1][i-1]+tmp[k-1][i+1]+tmp[k-2][i])&1){	//判断上一行是否为1 
			tmp[k][i] = 1;
			t++;
		}else
			tmp[k][i] = 0;
	}
	dfs(k+1,cur+t);
}
void getdfs(int k,int cur){
	if(k > m){
		dfs(2,cur);
		return;
	}
	tmp[1][k] = 0;//不翻转 
	dfs(k+1,cur);
	tmp[1][k] = 1;//翻转 
	dfs(k+1,cur+1);
}

int main(){	
std::ios::sync_with_stdio(false);  
#ifdef LOCAL
	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
#endif
	m=read(),n=read();
	memset(mp,0,sizeof(mp));
	memset(tmp,0,sizeof(tmp));
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			mp[i][j] = read();
	getdfs(1,0);
	if(nmin == INF)
		cout << "IMPOSSIBLE" << endl;
	else{
		for(int i=1;i<=m;i++){
			for(int j=1;j<=n;j++)
				cout << ans[i][j] << " ";				
			cout << endl;
		}
	}
	return 0;
}