关于LIS和memset()函数

LIS

关于最长上升子序列问题，有两种算法，复杂度 O（n^2） 和 O（nlogn）
导航----紫书P274，https://vjudge.net/problem/OpenJ_Bailian-2757

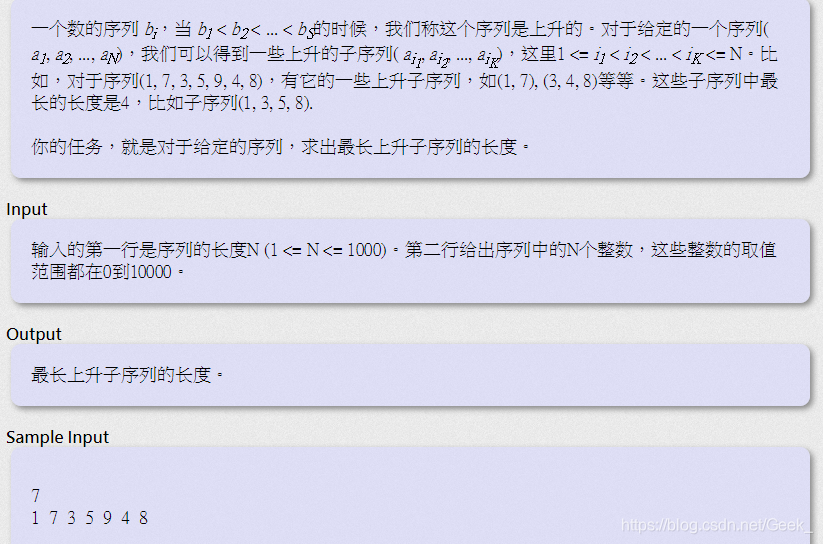
第一种

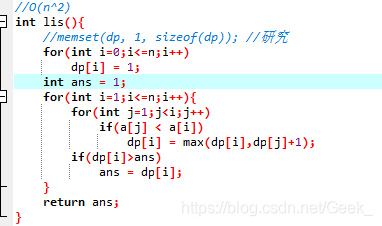
这一种，dp[i] = x 表示的是以i结尾的数的最长子序列是x，算法就是从第一个数开始遍历，再对前面的数进行遍历，再根据条件不断地更新dp[i]的值。
这个算法的主要在于内层循环浪费时间。

memset()

memset 函数是内存赋值函数，用来给某一块内存空间进行赋值的。
头文件：cstring 或 memory
话说刚开始使用memset的时候一直以为memset是对每一个int赋值的，心里想有了memset还要for循环对数组进行初始化干嘛。但其实memset这个函数的作用是将数字以单个字节逐个拷贝的方式放到指定的内存中去。

memset(dp,0,sizeof(dp))
int 类型的变量一般占用4个字节，对每一个字节赋值0的话就变成了“00000000 00000000 000000000 00000000” （即10进制数中的0）

memset(dp,1,sizeof(dp));
这样你可能以为如果你赋值1的话会让整个dp数组里的每一个int变成1，其实不然。
以上代码执行后，dp数组的内容为 00000001 00000001 00000001 00000001 转化为十进制后不为1。
所以不能直接用memset()函数对数组dp进行初始化！！！

改进算法

优化在于使用二分，让内层变成logn 的复杂度，可以利用lower_bound()函数，其复杂度是O(logn)。

思想：定义一个数组ans[i] = j; 表示长度为i时的结尾为j。初始化ans[1]=a[1]；再遍历数组，其中，对ans[]数组进行更新，如果a[i]>ans[len]的话，就长度加1，并把a[i]加入到数组ans中，当小于的时候，其实用到了贪心的思想，选择一个更小的数，让后面加入数的时候有更多的选择，因而将小的数更新大的数。