机器学习-线性回归详解
线性回归(Linear Regression)是机器学习中入门级但极其重要的算法之一。几乎所有监督学习模型,在思想或数学形式上,都能追溯到线性回归。它不仅是很多实际工程场景中的首选模型(如房价预测、销量预测、趋势分析等),也是理解损失函数、参数优化、梯度下降等核心概念的最佳切入点。本文将从直观理解 → 数学建模 → 公式推导 → 优化方法的角度,对线性回归进行系统、深入且“可读性强”的讲解
通俗的来说,我们的很多样本点分布在坐标轴上,线性回归要做的事,就是找到一条“最合适”的直线,穿过这些样本点。让更多的样本点落在这条直线上,而没有落在直线上的样本点则均匀的分布在直线两侧
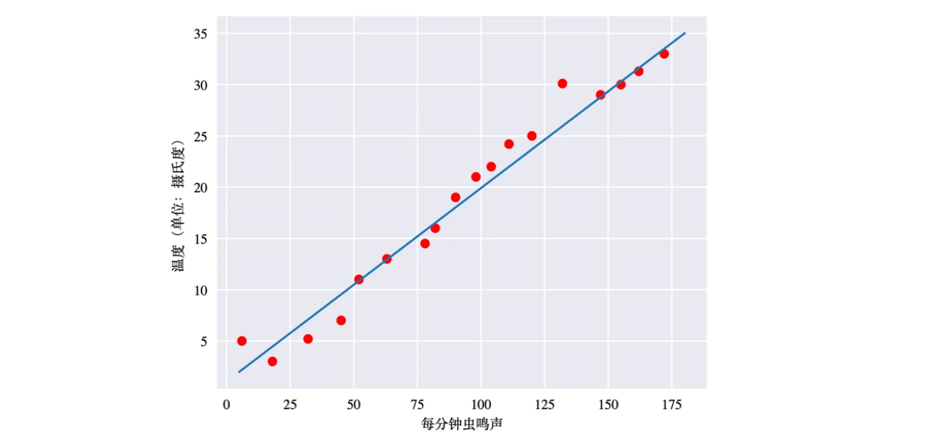
一元线性回归
所谓一元线性回归就是只有一列特征和一列标签的数据
| 身高(X) | 体重(Y) | |
|---|---|---|
| 1 | 160 | 56.3 |
| 2 | 166 | 60.6 |
| 3 | 172 | 66.4 |
| 4 | 174 | 68.5 |
| 5 | 180 | 75.0 |
| 6 | 176 | ?(预测) |
将特征写为X,预测结果为Y,就是使用一个变量 (x),预测一个结果 (y),而(y) 与 (x) 之间存在线性关系,那么就得到了一个一元函数:
y=wx+b
y = wx + b
y=wx+b
这里的w为权重,也叫斜率,决定直线的倾斜程度,而b为偏置,也叫截距,决定直线与 y 轴的交点,从几何角度看,这个模型本质上是在二维平面中拟合一条直线
以上面的数据集为例,将前五个样本代入公式中得到:
56.3 = 160w + b
60.6 = 166w + b
66.4 = 172w + b
68.5 = 174w + b
75.0 = 180w + b
通过这五条样本来计算出最合适的w和b,再通过Y = 176w + b就计算出了预测值
多元线性回归
然而在现实中,一个结果往往受到多个因素的影响。比如房价可能同时受到面积、楼层、房龄等多个特征的影响。此时我们就需要多元线性回归,即有多个特征列:
| 房子面积(x1) | 房子位置(x2) | 房子楼层(x3) | 房子朝向(x4) | 价格(y) | |
|---|---|---|---|---|---|
| 1 | 80 | 1 | 3 | 0 | 81 |
| 2 | 100 | 2 | 5 | 1 | 121 |
| 3 | 80 | 3 | 3 | 0 | 102 |
| … | … | … | … | … | … |
| n | 90 | 2 | 4 | 1 | 106 |
而每一个特征所对应的权重w是不同的,那么我们的模型可以写成:
y=w1x1+w2x2+⋯+wpxp+b=∑i=1pwixi
y = w_1 x_1 + w_2 x_2 + \dots + w_p x_p + b = \sum_{i=1}^p w_i x_i
y=w1x1+w2x2+⋯+wpxp+b=i=1∑pwixi
这里每个特征 xi 都对应一个权重 wi,表示该特征对预测结果的贡献程度;b 仍是全局偏置项。从几何角度看,一元回归是在二维空间拟合一条直线,而多元回归则是在 p+1 维空间中拟合一个超平面。
这里的特征列可以用一个向量表示:X=(x1,x2,…,xp)\mathbf{X} = (x_1, x_2, \dots, x_p)X=(x1,x2,…,xp),而所有的权重也可表示为一个向量:W=(w1,w2,…,wp)\mathbf{W} = (w_1, w_2, \dots, w_p)W=(w1,w2,…,wp),那么最终的模型函数可以表示为:
y=WTX+b
y = \mathbf{W}^T \mathbf{X} + b
y=WTX+b
如果令X=(1,x1,x2,…,xp)T\mathbf{X} = (1, x_1, x_2, \dots, x_p)^TX=(1,x1,x2,…,xp)T 为增广特征向量(加入常数项1),且W=(w0,w1,w2,…,wp)T\mathbf{W} = (w_0, w_1, w_2, \dots, w_p)^TW=(w0,w1,w2,…,wp)T 为增广权重向量,其中 w0=bw_0 = bw0=b,则多元线性回归模型可统一表示为:
y=WTX
y = \mathbf{W}^T \mathbf{X}
y=WTX
那么如何通过样本构建的模型来计算出 W 和 b 的最优组合呢?
损失函数
损失函数(Loss Function)用于衡量模型预测值与真实值之间的差距有多大,也叫代价函数、成本函数、目标函数
首先来了解误差的概念,用预测值 – 真实值就是误差:
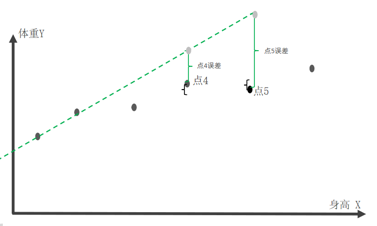
假设绿色为我们计算出来的拟合回归线,那么灰色的点就是基于模型的预测值,而黑色是数据的真实值,预测值 – 真实值就是该点的误差,而我们当然希望误差越小越好,误差越小,说明我们的拟合回归线所预测的结果更加接近真实值,那么损失函数就是基于各样本点的误差构建的函数,以便我们找到误差最小的拟合回归线,常见回归任务损失函数有:
-
均方误差(Mean Squared Error, MSE) :所有样本点误差平方和的平均值
L(y,y^)=1n∑i=1n(yi−y^i)2 L(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2 L(y,y^)=n1i=1∑n(yi−y^i)2 -
平均绝对误差(Mean Absolute Error, MAE):所有样本点误差绝对值和的平均值
L(y,y^)=1n∑i=1n∣yi−y^i∣ L(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^n |y_i - \hat{y}_i| L(y,y^)=n1i=1∑n∣yi−y^i∣ -
误差平方和(Sum of Squared Errors, SSE):所有样本点误差平方和
L(y,y^)=∑i=1n(yi−y^i)2 L(y, \hat{y}) = \sum_{i=1}^n (y_i - \hat{y}_i)^2 L(y,y^)=i=1∑n(yi−y^i)2
我们的目的就是要找到损失函数L(y,y^)L(y, \hat{y})L(y,y^)的极小值点,得到最优的权重向量W和偏置b,目前可以通过正规方程法和梯度下降法来求损失函数的极值点
正规方程法
在线性回归中,正规方程法(Normal Equation)是一种直接求解最优参数的解析方法,无需迭代(如梯度下降),核心是通过最小化损失函数,利用矩阵求导直接推导出参数的最优解
一元线性回归
以下损失函数采用误差平方和,基于一元线性回归的模型公式 y=wx+by = wx + by=wx+b,而 y^(i)\hat{y}^{(i)}y^(i)表示第i个样本预测值,y(i)y^{(i)}y(i)表示第i个样本真实值,那么损失函数可以表示为:
L(w,b)=∑i=1m(y^(i)−y(i))2=∑i=1m(wx(i)+b−y(i))2
L(w,b) = \sum_{i=1}^m \bigl(\hat{y}^{(i)} - y^{(i)}\bigr)^2 = \sum_{i=1}^m \bigl(wx^{(i)} + b - y^{(i)}\bigr)^2
L(w,b)=i=1∑m(y^(i)−y(i))2=i=1∑m(wx(i)+b−y(i))2
在数学中,寻找函数的极值点,就是令该函数求导后的值为0的点就是极值点,那么我们依次对w和b求偏导:
∂L(w,b)∂w=∑i=1m2(wx(i)+b−y(i))2−1⋅(wx(i)+b−y(i))′=∑i=1m(2wx(i)2+2bx(i)−2x(i)y(i))=0
\frac{∂L(w, b)}{∂w} = \sum_{i=1}^m 2\bigl(wx^{(i)} + b - y^{(i)}\bigr)^{2-1} \cdot \bigl(wx^{(i)} + b - y^{(i)}\bigr)' = \sum_{i=1}^m \bigl(2wx^{(i)2} + 2bx^{(i)} - 2x^{(i)}y^{(i)}\bigr) = 0
∂w∂L(w,b)=i=1∑m2(wx(i)+b−y(i))2−1⋅(wx(i)+b−y(i))′=i=1∑m(2wx(i)2+2bx(i)−2x(i)y(i))=0
∂L(w,b)∂b=∑i=1m2(wx(i)+b−y(i))2−1⋅(wx(i)+b−y(i))′ =∑i=1m(2wx(i)+2b−2y(i))=0
\frac{∂L(w, b)}{∂b}=\sum_{i=1}^m 2\bigl(wx^{(i)} + b - y^{(i)}\bigr)^{2-1} \cdot \bigl(wx^{(i)} + b - y^{(i)}\bigr)'\ = \sum_{i=1}^m \bigl(2wx^{(i)} + 2b - 2y^{(i)}\bigr) = 0
∂b∂L(w,b)=i=1∑m2(wx(i)+b−y(i))2−1⋅(wx(i)+b−y(i))′ =i=1∑m(2wx(i)+2b−2y(i))=0
将两式简化后得出:
w∑i=1mx(i)2+b∑i=1mx(i)−∑i=1mx(i)y(i)=0
w\sum_{i=1}^m x^{(i)2} + b\sum_{i=1}^m x^{(i)} - \sum_{i=1}^m x^{(i)}y^{(i)} = 0
wi=1∑mx(i)2+bi=1∑mx(i)−i=1∑mx(i)y(i)=0
w∑i=1mx(i)+bm−∑i=1my(i)=0
w\sum_{i=1}^m x^{(i)} + bm - \sum_{i=1}^m y^{(i)} = 0
wi=1∑mx(i)+bm−i=1∑my(i)=0
最后只需要带入真实样本数据,就得到了一个二元一次方程组,最终计算出w与b的最优值
多元线性回归
对于多元线性回归,已知模型公式为:y=w1x1+w2x2+⋯+wpxp+b=wTX+by = w_1 x_1 + w_2 x_2 + \dots + w_p x_p + b = \mathbf{w}^T \mathbf{X} + by=w1x1+w2x2+⋯+wpxp+b=wTX+b
数据集:D=(x1,y1),(x2,y2),...,(xn,yn)D = {(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), ..., (\mathbf{x}_n, y_n)}D=(x1,y1),(x2,y2),...,(xn,yn),其中 xi∈Rd\mathbf{x}_i \in \mathbb{R}^dxi∈Rd 是第 i 个样本的特征向量,yi∈Ry_i \in \mathbb{R}yi∈R 是标签
其中模型权重w是一个向量 w=w1,w2,w3,….wdw = {w_1, w_2, w_3, …. w_d}w=w1,w2,w3,….wd
那么第一个样本的损失为:
L1=(y^1−y1)2=(w1x11+w2x12+w3x13+⋯+wdx1d+b−y1)2=((∑j=1dwjx1j)+b−y1)2L1=(\hat{y}_1 - y_1)^2 = \bigl(w_1x_{11} + w_2x_{12} + w_3x_{13} + \dots + w_dx_{1d} + b - y_1\bigr)^2 = \left(\left(\sum_{j=1}^d w_jx_{1j}\right) + b - y_1\right)^2L1=(y^1−y1)2=(w1x11+w2x12+w3x13+⋯+wdx1d+b−y1)2=((j=1∑dwjx1j)+b−y1)2
n个样本样本损失最小: 相当于把第1个样本损失 + 第2个样本损失 + … 第n个样本的损失:
L(w,b)=∑i=1n(y^i−yi)2=∑i=1n(∑j=1dwjxij+b−yi)2
L(w,b)=\sum_{i=1}^n (\hat{y}_i - y_i)^2 = \sum_{i=1}^n \left( \sum_{j=1}^d w_j x_{ij} + b - y_i \right)^2
L(w,b)=i=1∑n(y^i−yi)2=i=1∑n(j=1∑dwjxij+b−yi)2
如果将线性预测关系转化为矩阵乘法,再用二范数表示误差平方和,并且将X和W通过上面讲到的方法变为增广特征向量和增广权重向量,(y^=WTX\hat{y} = \mathbf{W}^T \mathbf{X}y^=WTX)式子又可以表示为:
L(w)=∑i=1n(y^i−yi)2=∥y^−y∥22=∥Xw−y∥22
L(w) = \sum_{i=1}^n (\hat{y}_i - y_i)^2 = \|\hat{y} - y\|_2^2 = \|Xw - y\|_2^2
L(w)=i=1∑n(y^i−yi)2=∥y^−y∥22=∥Xw−y∥22
这里为什么写为了Xw\mathbf{X}\mathbf{w}Xw而不是wTX\mathbf{w}^T \mathbf{X}wTX,是为了矩阵乘法的维度兼容性 和 预测值向量的形式匹配。一个是单样本的向量点积形式,一个是多样本的矩阵批量计算形式,单样本是将w和x看作两个向量,而多样本时多个向量就组成了矩阵,而矩阵相乘需要遵循一定规则,因此产生了变化。
此时已知上面的损失函数,首先用二范数平方的矩阵展开损失函数:
L(w)=wTXTXw−2wTXTy+yTyL(w) = w^T X^T X w - 2w^T X^T y + y^T yL(w)=wTXTXw−2wTXTy+yTy
-
对 www 求导,应用矩阵求导的基本公式(二次项导数、一次项导数),对展开后的损失函数逐项求导,合并结果::
∂L∂w=2XTXw−2XTy\frac{\partial L}{\partial w} = 2X^T X w - 2X^T y∂w∂L=2XTXw−2XTy -
令导数为0,极值点满足导数为 0 的条件,因此将求导结果设为 0 向量,得到关于 w 的方程:
2XTXw−2XTy=02X^T X w - 2X^T y = 02XTXw−2XTy=0 -
化简得正规方程,消去方程两边的系数 2,整理得到线性回归的核心方程组(正规方程):
XTXw=XTyX^T X w = X^T yXTXw=XTy -
若 XTXX^T XXTX 可逆,在正规方程两边左乘其逆矩阵,消去左边的 XTXX^T XXTX,解得参数 w 的最优值:
w=(XTX)−1XTyw = (X^T X)^{-1} X^T yw=(XTX)−1XTy
接下来依旧是带入全部样本数据矩阵,求出最佳的www
梯度下降法
梯度下降是一种迭代式的优化算法,核心逻辑是沿着损失函数梯度下降的方向逐步更新参数,最终逼近线性回归的最优解。与直接通过矩阵求逆求解的正规方程相比,梯度下降具有显著的场景适配优势:更适合大数据与高维特征场景,正规方程需计算((XTX)−1)((X^TX)^{-1})((XTX)−1),矩阵求逆的时间复杂度为 (O(d3))(O(d^3))(O(d3)),当特征维度 d 大幅增加时计算量会呈指数级上升,而梯度下降每次迭代仅需 (O(nd))(O(nd))(O(nd)) 的计算成本,还支持小批量或随机迭代,内存占用极低
什么是梯度下降法,顾名思义:沿着梯度下降的方向求解极小值,举个例子:坡度最陡下山法
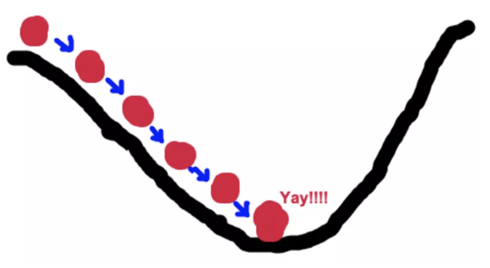
- 输入:初始化位置S;每步距离为a 。输出:从位置S到达山底
- 步骤1:令初始化位置为山的任意位置S
- 步骤2:在当前位置环顾四周,如果四周都比S高返回S;否则执行步骤3
- 步骤3: 在当前位置环顾四周,寻找坡度最陡的方向,令其为x方向
- 步骤4:沿着x方向往下走,长度为a,到达新的位置S‘S^‘S‘
- 步骤5:在S‘S^‘S‘位置环顾四周,如果四周都比S‘S^‘S‘高,则返回S‘S^‘S‘。否则转到步骤3
梯度
单变量函数中,梯度就是某一点切线斜率(某一点的导数);有方向为函数增长最快的方向
多变量函数中,梯度就是某一个点的偏导数;有方向:偏导数分量的向量方向
梯度下降公式:
循环迭代求当前点的梯度,更新当前的权重参数:θi+1=θi−α∂∂θiJ(θ)\theta_{i+1} = \theta_i - \alpha \frac{\partial}{\partial \theta_i} J(\theta)θi+1=θi−α∂θi∂J(θ)
α\alphaα 是学习率(步长) 不能太大, 也不能太小. 机器学习中:0.001 ~ 0.01,梯度是上升最快的方向, 我们需要是下降最快的方向, 所以需要加负号
一元线性回归
假如某个一元线性回归模型方程是J(θ)=θ2J(\theta) = \theta^2J(θ)=θ2
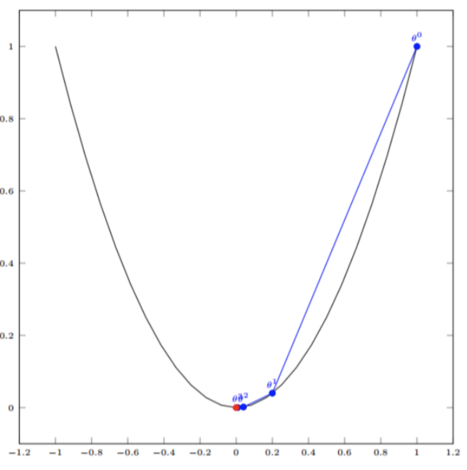
那么J(θ)J(\theta)J(θ)函数关于 θ\thetaθ 的导数为: 2θ2\theta2θ,初始化起点为1 ,学习率 α\alphaα = 0.4
们开始进行梯度下降的迭代计算过程:
- 第一步:θ\thetaθ = 1
- 第二步:θ\thetaθ = θ\thetaθ - α\alphaα * (2θ2\theta2θ) = 1 - 0.4 * (2*1) = 0.2
- 第三步:θ\thetaθ = θ\thetaθ - α\alphaα * (2θ2\theta2θ) = 0.2 - 0.4 * (2*0.2) = 0.04
- 第四步:θ\thetaθ = θ\thetaθ - α\alphaα * (2θ2\theta2θ) = 0.04 - 0.4 * (2*0.04) = 0.008
- 第五步:θ\thetaθ = θ\thetaθ - α\alphaα * (2θ2\theta2θ) = 0.008 - 0.4 * (2*0.008) = 0.0016
… - 第N步:θ\thetaθ 已经极其接近最优值 0,J(θ)J(\theta)J(θ) 也接近最小值。
多元线性回归
假如某个d多元线性回归模型方程是:J(θ)=θ12+θ22J(\theta) = \theta_1^2 + \theta_2^2J(θ)=θ12+θ22
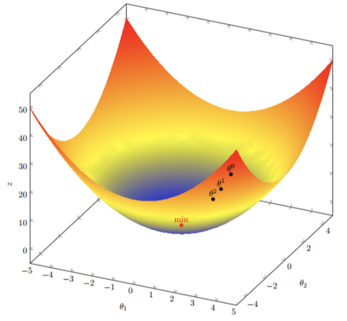
J(θ)J(\theta)J(θ)函数关于 θ1\theta_1θ1的导数为: 2θ12\theta_12θ1 ,J(θ)J(\theta)J(θ) 函数关于 θ2\theta_2θ2 的导数为: 2θ22\theta_22θ2, 则 J(θ)J(\theta)J(θ)的梯度为:(2θ1,2θ2)(2\theta_1,2\theta_2)(2θ1,2θ2) 初始化起点为: (1, 3) 学习率 α\alphaα = 0.1
- 第一步:(θ1,θ2)=(θ1,θ2)−α⋅(2θ1,2θ2)=(θ1−α⋅2θ1,θ2−α⋅2θ2)=(1−0.1⋅2,3−0.1⋅6)=(0.8,2.4)(\theta_1, \theta_2) = (\theta_1, \theta_2) - \alpha \cdot (2\theta_1, 2\theta_2) = (\theta_1 - \alpha \cdot 2\theta_1, \theta_2 - \alpha \cdot 2\theta_2) = (1-0.1 \cdot 2, 3-0.1 \cdot 6)=(0.8, 2.4)(θ1,θ2)=(θ1,θ2)−α⋅(2θ1,2θ2)=(θ1−α⋅2θ1,θ2−α⋅2θ2)=(1−0.1⋅2,3−0.1⋅6)=(0.8,2.4)
- 第二步:(θ1,θ2)=(θ1,θ2)−α⋅(2θ1,2θ2)=(θ1−α⋅2θ1,θ2−α⋅2θ2)=(0.8−0.1⋅1.6,2.4−0.1⋅4.8)=(0.64,1.92)(\theta_1, \theta_2) = (\theta_1, \theta_2) - \alpha \cdot (2\theta_1, 2\theta_2) = (\theta_1 - \alpha \cdot 2\theta_1, \theta_2 - \alpha \cdot 2\theta_2) = (0.8-0.1 \cdot 1.6, 2.4-0.1 \cdot 4.8)=(0.64, 1.92)(θ1,θ2)=(θ1,θ2)−α⋅(2θ1,2θ2)=(θ1−α⋅2θ1,θ2−α⋅2θ2)=(0.8−0.1⋅1.6,2.4−0.1⋅4.8)=(0.64,1.92)
… - 第N步: θ1\theta_1θ1、 θ2\theta_2θ2 已经极其接近最优值,J(θ)J(\theta)J(θ) 也接近最小值。





















 1507
1507

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








