机器学习基础 | KNN（K-近邻）

机器学习基础 | KNN（K-近邻）

---

KNN（K-Nearest Neighbor，K 近邻算法）是最简单、最经典的机器学习算法之一。它不依赖复杂的数学模型，而是依靠“邻居的选择”来进行分类与回归，因此非常直观易懂。本博客将从算法思想、流程、距离度量、特征工程、代码，到 KNN 在鸢尾花识别中的应用，进行全方位解析。

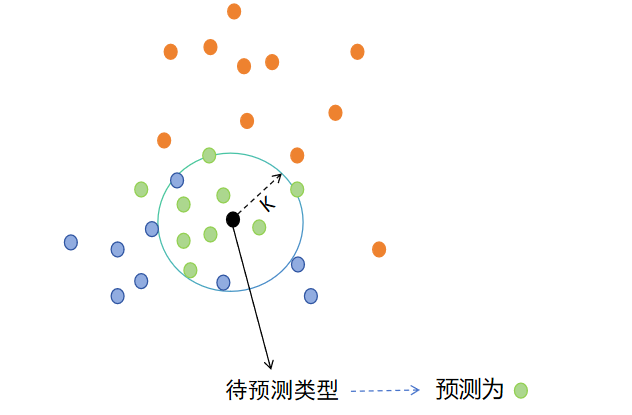
🔍KNN算法简介

它的本质是一种 基于相似度度量的监督学习方法，通过计算样本之间的“距离”来判断类别或预测数值。虽然算法看起来简单，但其背后蕴含的思想却非常深刻，并在科学研究和工业应用中仍被广泛使用。

它的核心理念可以用一句话概括：

物以类聚，人以群分——一个样本最接近的 K 个邻居是什么类别，它自己就是什么类别。

换句话说，如果你搬到一个新小区，你很可能会受到周围邻居的影响：
如果附近的人大多数喜欢健身，你可能也会去健身房；
如果周围邻居大多从事互联网行业，你可能也会被“归类”为技术从业者。

这，就是 KNN 的思想。

KNN既可以用于回归算法，也可以用于分类算法

---

👉KNN 的算法流程

1. 计算未知样本与所有训练样本的距离

2. 按距离升序排序

3. 取最近的 K 个邻居

4. 采用 多数投票法（Majority Voting）

5. 将未知样本归入出现次数最多的类别

以上是用与做分类预测，而回归模型只需要将第四步中的多数投票法变为计算平均值就可以了

那么如何计算样本之间的距离呢？

---

🎯距离计算方法

KNN 通过计算样本之间的“距离”来衡量相似度。

常见的距离计算方法有

• 欧氏距离
• 曼哈顿距离
• 切比雪夫距离
• 闵可夫斯基距离

这里讲解最常用的欧氏距离：对应维度之间的差值平方和开方

欧氏距离的公式是：
$$d(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$
这里有一份关于电影类型预测的数据集，根据不同镜头的数量来判断该电影的类型，前9个电影给出了标签值

序号	电影名称	搞笑镜头	拥抱镜头	打斗镜头	电影类型
1	功夫熊猫	39	0	31	喜剧片
2	叶问3	3	2	65	动作片
3	伦敦陷落	2	3	55	动作片
4	代理情人	9	38	2	爱情片
5	新步步惊心	8	34	17	爱情片
6	谍影重重	5	2	57	动作片
7	功夫熊猫	39	0	31	喜剧片
8	美人鱼	21	17	5	喜剧片
9	宝贝当家	45	2	9	喜剧片
10	唐人街探案	23	3	17	？

要预测第十个电影唐人街探案的电影类型，那么功夫熊猫和他的距离计算就是：
$$\sqrt{(39-23{)}^2+(0-3{)}^2+(31-17{)}^2}=21.47$$
那么这两个样本之间的距离就是21.47，将给出标签的9部电影全部计算出与其的距离，找出距离他最近的K个样本，看这K个样本中哪个类型最多，那么就对其预测为该种类型

KNN分类简单代码示例：

# 导入KNN分类算法模型
from sklearn.neighbors import KNeighborsClassifier

# 数据集
x_train = [[39, 0, 31], [3, 2, 65], [2, 3, 55], [9, 38, 2]]      # 训练集特征数据
y_train = [0, 1, 1, 2]                          				 # 训练集标签数据
x_text = [[23, 3, 17]]                               			 # 测试集特征数据

# 创建模型对象，这里传参是K值为2
estimator = KNeighborsClassifier(n_neighbors=2)

# 训练模型
estimator.fit(x_train, y_train)

# 模型预测
y_pred = estimator.predict(x_text)
print(f'预测值为: {y_pred}')

那么这个K值该如何选取呢？

• K 太小：容易受噪声干扰，过拟合

• K 太大：影响平均化，欠拟合

这个K值在机器学习中叫做超参

---

📘 交叉验证（Cross Validation）与网格搜索（Grid Search）

在机器学习任务中，模型的好坏不仅取决于数据质量和算法本身，还高度依赖于 超参数（Hyperparameters） 的选择。像 KNN 中的 K 值、距离度量方式、权重策略等，都属于超参数，而这些参数往往不能通过训练自动学习，需要人工指定。

一个模型因超参数选择不当而导致表现不佳，是非常常见的问题。因此，我们需要系统、可靠的方法来“选参数”，交叉验证和网格搜索正是解决这一问题的两大利器。

交叉验证

交叉验证是一种用于评估模型性能的可靠方法，它通过将训练数据分成若干份（如 5 份或 10 份），并让每一份数据都轮流充当一次“验证集”，其余数据用于训练，从而不断重复训练与评估，最终将多个评估结果取平均值，得到一个更稳定、更可信的模型性能评分。与单次划分相比，交叉验证避免了因数据划分偶然性导致的结果波动，减少了过拟合风险，并让每条数据都得以被充分利用，是机器学习中最常用、最科学的模型评估方式之一

交叉验证最常见的是 K 折交叉验证（K-Fold Cross Validation）。

例如：K = 5（5-fold）

整个数据集会被平均分成 5 份：

训练集	测试集
1,2,3,4	5
1,2,3,5	4
1,2,4,5	3
1,3,4,5	2
2,3,4,5	1

每一次：

用 4 份训练——>用 1 份验证——>重复 5 次——>最后把 5 次的验证精度取平均值

例如：

折数	精度
1	93%
2	95%
3	92%
4	94%
5	93%

最终模型的评分为：
$$score=93+95+92+94+935=93.4$$

这种方式得到的评估结果具有以下优点：

• ✔ 数据利用率高

  每份数据都当过训练数据，也当过验证集。

• ✔ 结果更稳定

  不再依赖单次划分而带来的偶然性。

• ✔ 泛化能力更可靠

  平均结果更反映模型的真实能力。

网格搜索

网格搜索是一种系统化的超参数搜索方法，它会把人为设定的所有参数组合列成一个“网格”，然后让模型逐一用这些参数组合进行训练，并通过交叉验证来评估每组组合的表现，从而最终找到效果最好的那一组参数。网格搜索让调参从“靠经验猜”转变为“由机器穷举验证”，是一种全面、自动、可重复的参数优化方式，尤其适用于像 KNN 这样受超参数影响较大的算法

这就像你去商场买衣服：

• 每件衣服有不同尺寸（S/M/L）
• 不同颜色（红/白/黑）
• 不同材质（棉/麻/丝）

你可能会：把所有可能的组合试一遍，再选出最满意的那一套

搭配使用，找出最优超参

例如：

param_grid = {
    "n_neighbors": [1, 3, 5, 7, 9],
    "weights": ["uniform", "distance"],
    "p": [1, 2]
}

sklearn 会依次测试：

K=1, uniform, p=1
K=1, uniform, p=2
K=1, distance, p=1
K=1, distance, p=2
K=3, uniform, p=1
...

假设共有 5 × 2 × 2 = 20 组参数
如果你设置了 5 折交叉验证

则：

20 组参数 × 5 次训练与评估 = 100 次模型训练

最终得到一组最优参数，例如：

n_neighbors = 3
weights = "distance"
p = 2

---

利用KNN算法对鸢尾花分类

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris  # 鸢尾花数据集
import seaborn as sns  #
import pandas as pd
import matplotlib.pyplot as mlb
from sklearn.model_selection import train_test_split  # 分割训练集和测试集
from sklearn.preprocessing import StandardScaler  # 特征标准化模型
from sklearn.neighbors import KNeighborsClassifier  # KNN分类算法
from sklearn.metrics import accuracy_score  # 做模型评估，计算模型预测的准确率


# 实现鸢尾花完整案例
def knn_iris():
    # 1.加载数据集
    iris_data = load_iris()

    # 2.数据预处理,这里切分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2,
                                                        random_state=13)

    # 3.特征工程
    transfer = StandardScaler()  # 创建标准化对象
    x_train = transfer.fit_transform(x_train)  # fit_transform兼具训练和转换，让标准化对象更契合数据集，一般用于处理训练集
    x_test = transfer.transform(x_test)  # transform函数只有转换，适用于测试集的标准化

    # 4.模型训练
    estimator = KNeighborsClassifier(n_neighbors=6)  # 超参
    estimator.fit(x_train, y_train)  # 模型训练

    # 5.模型预测
    # 5.1 对切分的训练集进行预测
    y_pre = estimator.predict(x_test)  # 预测
    print(f'预测结果为:{y_pre}')

    # 5.2 对新的数据集进行预测
    my_data = [[7.8, 2.5, 6.9, 0.15]]  # 自己拟写一些数据
    my_data = transfer.transform(my_data)  # 之前做了特征标准化，那么新数据也得做
    my_pre = estimator.predict(my_data)
    print(f'新数据预测为:{my_pre}')

    my_data_proba = estimator.predict_proba(my_data)  # 查看该数据集对于每种分类的预测概率
    print(f'各分类的预测概率为:{my_data_proba}')

    # 6.模型评估
    # 方式1:直接评分，基于训练集特征和训练集标签
    print(f'准确率为:{estimator.score(x_train, y_train)}')

    # 方式2:基于测试集的标签和预测结果进行评分
    print(f'准确率为:{accuracy_score(y_test, y_pre)}')  # 传入测试集的标签和预测结果


if __name__ == '__main__':
    knn_iris()