高光谱图像去噪（一）

传统的逐波段的对每个灰度图像进行去噪，如基于非局部的算法、SVD、BM3D等。忽略了不同光谱波段之间的强相关性，去噪性能差。

存在的问题：

1）不同波段的噪声强度往往是不同的，某些波段可能会倍强噪声污染，需要在对低信噪比的波段去噪的同时保护高信噪比波段；

2）噪声通常是混合存在的，如高斯噪声、条带噪声、脉冲噪声等，不同噪声的特性和分布特征也不同。

结合空间和光谱信息的去噪方法：基于变换域和基于空间域两种。

基于变换域：小波变换、PCA、傅里叶变换，性能依赖于变换函数的选择；

基于空间域：分为滤波器和正则化两种。

a、基于滤波器的方法将高光谱数据是为一个完整的三维立方体（三维张量），使用张量分解法去噪。

b、基于正则化方法通过先验知识建立模型，如稀疏表示、全变分（TV）、稀疏矩阵分解、低秩表示等。

全变分正则化（TV）可以有效保留形状边缘并增强分段平滑度，消除单一噪声效果较好。

高光谱图像的噪声退化模型：

Y=X+S+N

其中，X为纯净图像，S为稀疏噪声，N为零均值的高斯噪声。Y、X、S、N大小均为M*N*P，M*N为空间尺寸，P为波段数。

将高光谱每个波段的图像转换为具有MN个元素的列向量，即

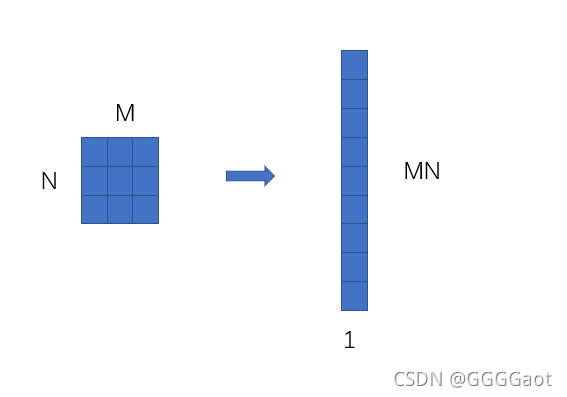
 最终得到一个大小为MN*P的二维矩阵。

高光谱图像去噪是一个从三维张量Y中分理出稀疏噪声S和高斯噪声N得到纯净图像X的过程。常用的求解思路是添加未知的高光谱图像和混合早生的先验信息。在此框架下进行去噪，最广泛应用的方法为鲁棒主成分分析法（RPCA）。

稀疏表示

稀疏表示，就是使用尽量少的基对原始信号进行表示。原始基（原子）组成的集合即为字典，字典具有高度冗余性。

对于一幅噪声图像Y=X+N，可通过

进行求解。

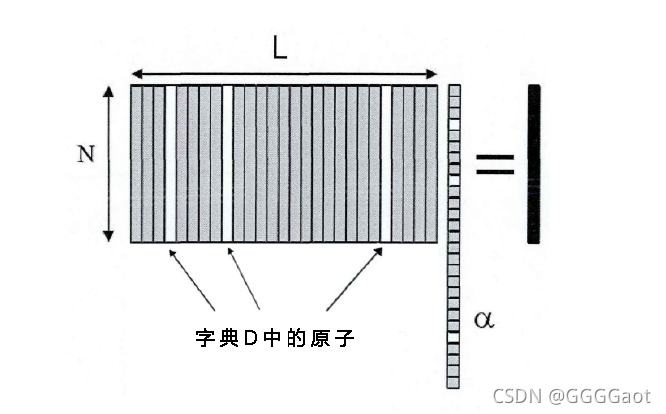
 X是由D的原子线性组合得到的，a中的绝大多数元素均为0，则X=Da。

X在D上的稀疏表示，可以通过对Y的估计得到：

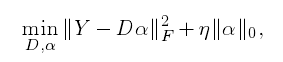
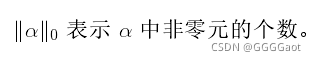
 得到D的过程被称为字典学习，得到a的过程被称为稀疏编码。

 加权核范数

基于核范数最小化的低秩刻画在图像去噪中得到了广泛研究。存在的问题是大部分基于核范数最小化的低秩刻画在求解的过程中对每一个奇异值都进行同等对待。一般地，较大的奇异值代表图像的主要特征，较小的奇异值代表噪声部分。因此在削减奇异值的过程中应削减小奇异值保留大奇异值。