最近公共祖先总结

最近公共祖先

引入

最近公共祖先简称 $LCA（LowestCommonAncestor）$。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。 为了方便，我们记某点集 S = { v 1 , v 2 , … , v n } S=\{v_1,v_2,\ldots,v_n\} S={v1​,v2​,…,vn​} 的最近公共祖先为 $\text{LCA}(v_1,v_2,\dots ,v_n)$ 或 $\text{LCA}(S)$。

对于有根树 $T$ 的两个结点 $u,v$，最近公共祖先 $LCA(T,u,v)$ 表示一个结点 $x$ ，满足 $x$ 是 $u$ 和 $v$ 的祖先且 $x$ 的深度尽可能大。在这里，一个节点也可以是它自己的祖先。——摘自百度

做法

朴素做法

过程

法一

每次找深度较大的那个点，顺着树往上跳，并在经过的路径留下标记。再找另外一个点，同样顺着树往上跳，第一次碰到有标记的节点，该节点就是两个节点的 $LCA$。

法二

找两个点，让深度较大的那个点跳到与另一个点相同的深度，然后两个点同时往上跳，两个点第一次相遇所在的节点，就是两点的 $LCA$。

性质

在同棵个树上，这两个点最后一定会在一个节点相遇，这个相遇的点就是这两个点的最近公共祖先(LCA)。

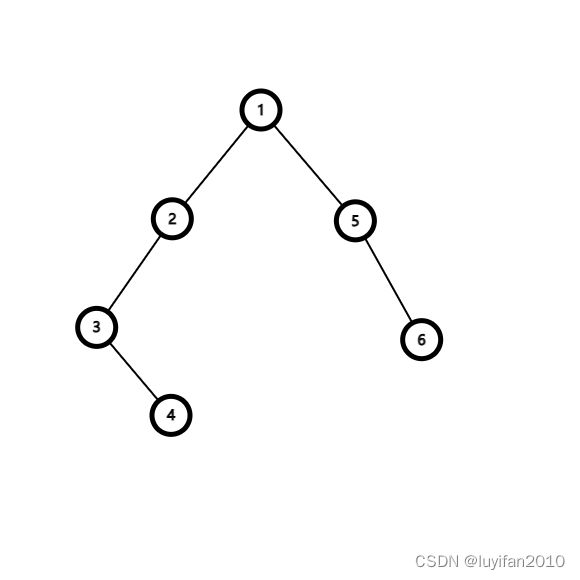
以上两种算法在遍历树时，最坏的时间复杂度是 $O(n)$，此时的树应是这样的

树上倍增

过程

倍增，即以 $1,2,4,8,16,32\dots$ 这种规律来增大，将其运用到上面的朴素算法中，就是将每次跳的步数转化为跳 $2$ 的次方步，只不过我们要将 $2$ 的次方从大到小来跳，即所跳步数为 $2^k,2^{k-1},\dots ,2^3,2^2,2^1,2^0$，一旦跳过了目标节点，就换一个更小的 $2$ 的次方步来跳，直到跳到目标节点为止。

想要将以上思路转化为算法，还需提前处理一下每个节点的深度和他们 $2$ 的次方级的祖先，其中， $dep[i]$ 表示第 $i$ 个节点的深度，$f[i][j]$ 表示第 $i$ 个节点的 $2^j$ 级的祖先的编号，我们用深搜来完成这个操作。

void dfs(int u,int fa){
	dep[u]=dep[fa]+1;
	for(int i=head[u];i;i=edge[i].next){//遍历节点u的所有孩子 
		int j=edge[i].v;
		if(j==fa)continue;
		f[j][0]=u;
		for(int k=1;(1<<k)<=dep[u];k++){//计算f数组，他最多到根节点 
			f[j][k]=f[f[j][k-1]][k-1];
		}
		dfs(j,u);//继续往下深搜 
	}
	return;
}

在预处理完各个节点所需的信息后，则可以通过倍增思想来求 $LCA$ 了

与朴素算法的法二十分相似，先让两个点处于同一个高度，然后倍增步数往上跳

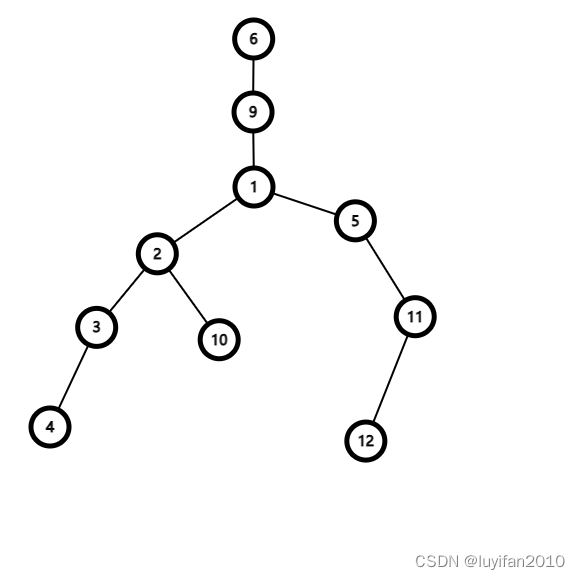
在上图中若跳到点 $2$ 和 $11$ 时，一不小心跳过了点 $1$ 到了点 $9$，虽然两点此时相同，但点 $9$ 只是两点的公共祖先，并不是 $LCA$ ，所以我们要将两点跳到 $2$ 和 $5$ ，即跳到 $LCA$ 的下面一层，最后输出两点的父节点即可。

int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);//让x成为深度最大的那个节点 
	for(int i=19;i>=0;i--){//算法关键1，用倍增让x调到和y同一层 
		if(dep[f[x][i]]>=dep[y]){
			x=f[x][i];
		}
	}
	if(x==y)return y;//两个点同一层时处于同一节点，则当前节点为其LCA，此时x是y的祖先
	for(int i=19;i>=0;i--){//如果x跳过头了，就换一个小的i重跳 
		if(f[x][i]!=f[y][i]){//目标x和y调到其最近公共祖先的下一层 
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];//返回答案 
}

性质

倍增算法的预处理时间复杂度为 $O(n\log n)$，单次查询时间复杂度为 $O(\log n)$。 倍增算法可以通过交换 $f$ 数组的两维使较小维放在前面。这样可以提高程序效率。

$Tarjan$离线算法

$Tarjan$是一种离线算法，一次性读入所有查询后再进行问题的求解，利用了并查集来储存祖先节点

做法

1. 从根节点出发对树进行遍历，将访问过的节点进行标记
2. 当某一节点 $u$ 的所有子节点被访问过之后，检查所有和 $u$ 有关的查询（已提前存入 $vec$ 数组中），若存在一个查询 $u,v$ 并且 $vis[v]==true$ ，则利用并查集查询 $v$ 的祖宗，查询到的祖宗节点就是 $u,v$ 的 $LCA$。

int find(int x){//并查集查找根节点 
	if(fa[x]!=x)fa[x]=find(fa[x]);
	return fa[x];
}
void tarjan(int u){
	vis[u]=true;//标记访问过 
	for(int i=head[u];i;i=edge[i].next){
		int j=edge[i].v;
		if(!vis[j]){
			tarjan(j);
			fa[j]=u;
		}
	}
	for(int i=0;i<vec[u].size();i++){
		int y=vec[u][i].first;
		int id_=vec[u][i].second;
		if(vis[y])res[id_]=find(y);
	}
	return;
}

一道例题

最近公共祖先
一道模板题，放一下倍增和 $Tarjan$ 的写法。

倍增法

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5e5+10;
struct Edge{
	int v,next;
}edge[maxn*2];
int head[maxn],idx=1;//邻接表储存树 
int n,m,root;//分别表示节点个数，询问个数，根节点标号 
int f[maxn][20];//f(i,j)号节点网上跳2^j步的节点编号 
int dep[maxn];//节点i的深度，规定根节点的深度为1 
void connec(int x,int y){
	edge[idx].v=y;
	edge[idx].next=head[x];
	head[x]=idx++;
	return;
}
void dfs(int u,int fa){
	dep[u]=dep[fa]+1;
	for(int i=head[u];i;i=edge[i].next){//遍历节点u的所有孩子 
		int j=edge[i].v;
		if(j==fa)continue;
		f[j][0]=u;
		for(int k=1;(1<<k)<=dep[u];k++){//计算f数组，他最多到根节点 
			f[j][k]=f[f[j][k-1]][k-1];
		}
		dfs(j,u);//继续往下深搜 
	}
	return;
}
int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);//让x成为深度最大的那个节点 
	for(int i=19;i>=0;i--){//算法关键1，用倍增让x调到和y同一层 
		if(dep[f[x][i]]>=dep[y]){
			x=f[x][i];
		}
	}
	if(x==y)return y;
	for(int i=19;i>=0;i--){//如果x跳过头了，就换一个小的i重跳 
		if(f[x][i]!=f[y][i]){//目标x和y调到其最近公共祖先的下一层 
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];//返回答案 
}
signed main(){
	int x,y;
	scanf("%lld%lld%lld",&n,&m,&root);
	for(int i=1;i<n;i++){//读入一棵树，用邻接表储存起来
		scanf("%lld%lld",&x,&y);
		connec(x,y);
		connec(y,x);
	}
	dfs(root,0);//计算每个节点的深度，并且预处理f数组 
	for(int i=1;i<=m;i++){
		scanf("%lld%lld",&x,&y);
		printf("%lld\n",lca(x,y));//计算两个点的lca 
	}
	return 0;
}

$Tarjan$法

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5e5+10;
typedef pair<int,int>pll;//第一个元素为节点编号，第二个元素为询问编号 
struct Edge{
	int v,next;
}edge[maxn*2];
int head[maxn],idx=1;//邻接表存储树 
int fa[maxn];//并查集数组 
int n,m,root;//分别表示节点个数、询问个数、根节点编号 
vector<pll> vec[maxn];//储存下来所有询问 vec[x]:代表和 x节点有关的询问，即第 vec[x].second个询问 LCA(x,vec[x].first) 
int res[maxn];//结果，把第 i次询问的结果放进 res[i]里面
bool vis[maxn];//标记数组 
void connec(int x,int y){
	edge[idx].v=y;
	edge[idx].next=head[x];
	head[x]=idx++;
	return;
}
int find(int x){//并查集查找根节点 
	if(fa[x]!=x)fa[x]=find(fa[x]);
	return fa[x];
}
void tarjan(int u){
	vis[u]=true;//标记访问过 
	for(int i=head[u];i;i=edge[i].next){
		int j=edge[i].v;
		if(!vis[j]){
			tarjan(j);
			fa[j]=u;
		}
	}
	for(int i=0;i<vec[u].size();i++){
		int y=vec[u][i].first;
		int id_=vec[u][i].second;
		if(vis[y])res[id_]=find(y);
	}
	return;
}
signed main(){
	int x,y;
	scanf("%lld%lld%lld",&n,&m,&root);
	for(int i=1;i<n;i++){//读入一棵树，用邻接表存储起来 
		scanf("%lld%lld",&x,&y);
		connec(x,y);
		connec(y,x);
	}
	for(int i=1;i<=n;i++)fa[i]=i;//并查集初始化 
	for(int i=1;i<=m;i++){//把 m次询问存下来 
		scanf("%lld%lld",&x,&y);
		vec[x].push_back({y,i});
		vec[y].push_back({x,i});
	}
	tarjan(root);//调用 tarjan算法 
	for(int i=1;i<=m;i++)printf("%lld\n",res[i]);
	return 0;
}