字典树总结

字典树 (Trie)

定义

字典树，英文名$trie$。顾名思义，就是一个像字典一样的树。

又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。——摘自百度

引入

先放一张图

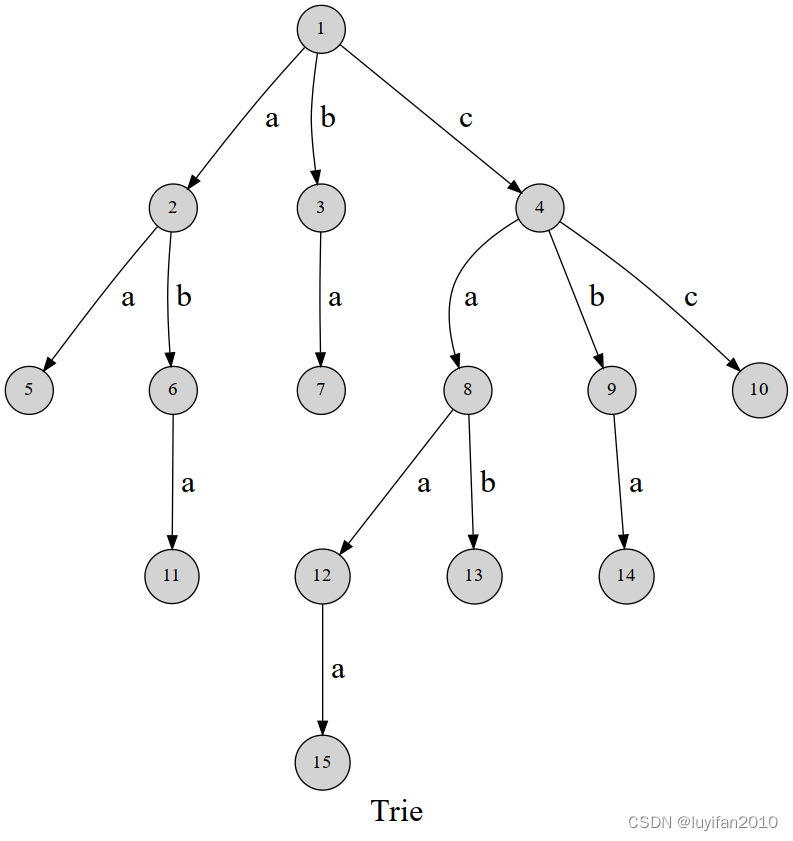
很容易在图中发现，字典树的边代表字母，从根结点到树上某一结点的路径就代表了一个字符串。

比如说，$1\to 4\to 9\to 14$ 表示的就是字符串 $cba$。

$trie$的结构非常好懂，我们用$(u,c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点，或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。（$c$ 的取值范围和字符集大小有关，不一定是 $0\sim 26$。）

有时需要标记插入进 $trie$ 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可（不一定是赋值）。

字典树例题

题面
维护一个字符串集合，支持两种操作：
$I$ $x$ 向集合中插入一个字符串 $x$；
$Q$ $x$ 询问一个字符串在集合中出现了多少次。
共有 $N$ 个操作，所有输入的字符串总长度不超过 $10^5$，字符串仅包含小写英文字母。
输入格式
第一行包含整数 $N$，表示操作数。$1\le N\le 2e4$
输出格式
对于每个询问指令 $Q$ $x$，都要输出一个整数作为结果，表示 $x$ 在集合中出现的次数。
每个结果占一行。
输入/输出例子
输入：
5
I abc
Q abc
Q ab
I ab
Q ab
输出：
1
0
1

这是一道模板题，下面的代码中有两个关键函数 $insert$ 和 $find$，其功能分别为插入字符串和查找字符串

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e5+10,maxm=26+10;
int nex[maxn][maxm],cnt[maxn],n,idx;
void insert(string s){//插入字符串 
	int p=0,len=s.size();
	for(int i=0;i<len;i++){
		int tmp=s[i]-'a'+1;
		if(!nex[p][tmp])nex[p][tmp]=++idx;//如果不存在则插入 
		p=nex[p][tmp];//继续往下查找 
	}
	cnt[p]++;//打标记 
	return;
}
int find(string s){//查找函数 
	int p=0,len=s.size();
	for(int i=0;i<len;i++){
		int tmp=s[i]-'a'+1;
		if(nex[p][tmp])p=nex[p][tmp];//存在，继续往下走 
		else return 0;//不存在 
	}
	return cnt[p];
}
signed main(){
	string op,s;
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		cin>>op>>s;
		if(op=="I")insert(s);
		else printf("%lld\n",find(s));
	}
	return 0;
}