[HackerRank]BFS Shortest Reach in a Graph

BFS: Shortest Reach in a Graph

Challenge Name: BFS: Shortest Reach in a Graph

Consider an undirected graph consisting of $n$ nodes where each node is labeled from $1$ to $n$ and the edge between any two nodes is always of length $6$. We define node $s$ to be the starting position for a BFS. Given a graph, determine the distances from the start node to each of its descendants and return the list in node number order, ascending. If a node is disconnected, it’s distance should be $-1$.
For example, there are $n = 6$ nodes in the graph with a starting node $s = 1$. The list of $edges = [[1,2],[2,3],[3,4],[1,5]]$, and each has a weight of $6$.

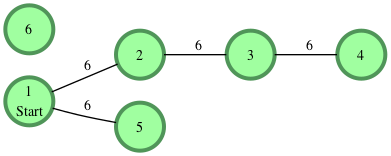
Starting from node $1$ and creating a list of distances, for nodes $2$ through $6$ we have $distances = [6, 12, 18, 6, -1]$.
Function Description
Define a Graph class with the required methods to return a list of distances.

这道题要求用广度优先遍历图，找到两个节点的最短路径。之前复习了广度优先，实现的办法是引入一个队列。至于图的实现办法，就是用一个二维矩阵，建立两点的映射，两点相连的话该值就为1，不相连为0。

在HackerRank上面做题很头疼的一点是它会给出一些巨大的测试集，无脑用vector的话很容易timeout，就像Merge Sort Counting Inversions里面经历的，这次我也经历了timeout，好在最后都解决了。这一次导致超时的地方是在bfs中，我们会检测节点是否已经经过。最开始我无脑的把整个图复制了vector<vector<int>> seen(graph)，而这显然是没有必要的，我们只需要一个长度为n的vector就足够。

做题过程中遇到的另一个问题是distances的记录，最初我用一个count变量，每pop一次就+1，但这会导致count记录的是经过的全部节点数，而不是节点的层数。

#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

class Graph {
    int n;
    vector<vector<int>> graph;
public:
    Graph(int n) {
        vector<int> tmp(n, 0);
        for (int i = 0; i < n; i++) {
            graph.push_back(tmp);
        }
        this->n = n;
    }

    void add_edge(int u, int v) {
        graph[u][v] = 1;
        graph[v][u] = 1;
    }

    int bfs(int start, int end) {
        vector<int> seen(n);
        queue<int> que;
        que.push(start);
        seen[start] = 1;
        int distances[n] = {0};
        while (!que.empty()) {
            for (int i = 0; i < n; i++) {
                if (graph[que.front()][i] == 1 && seen[i]==0) {
                    distances[i] = distances[que.front()]+6;
                    if (i == end) return distances[i];
                    que.push(i);
                    seen[i] = 1;
                }
            }
            que.pop();
        }
        return -1;
    }

    vector<int> shortest_reach(int start) {
        vector<int> res;
        for (int i = 0; i < n; i++) {
            res.push_back(bfs(start, i));
        }
        return res;
    }



};

int main() {
    int queries;
    cin >> queries;

    for (int t = 0; t < queries; t++) {

        int n, m;
        cin >> n;
        // Create a graph of size n where each edge weight is 6: 
        Graph graph(n);
        cin >> m;
        // read and set edges
        for (int i = 0; i < m; i++) {
            int u, v;
            cin >> u >> v;
            u--, v--;
            // add each edge to the graph
            graph.add_edge(u, v);
        }
        int startId;
        cin >> startId;
        startId--;
        // Find shortest reach from node s
        vector<int> distances = graph.shortest_reach(startId);

        for (int i = 0; i < distances.size(); i++) {
            if (i != startId) {
                cout << distances[i] << " ";
            }
        }
        cout << endl;
    }

    return 0;
}