基于PID控制器和卡尔曼滤波器的机器人控制（Matlab代码实现）

原创于 2025-12-04 00:38:46 发布 · 756 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#机器人 #matlab #算法 #支持向量机

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

目标是使用线性卡尔曼滤波器估计速度，并使用PID控制器控制机器人。

考虑一个在无摩擦、笔直的车道上的机器人。最初，机器人静止在位置 0。我们每 \Delta t 秒测量一次机器人的位置，但这些测量并不精确;我们希望保持机器人位置和速度的模型。

我们在这里展示如何推导创建卡尔曼滤波器的模型。由于 F、H、R 和 Q 是恒定的，因此它们的时间指数被删除。

机器人的位置和速度由线性状态空间描述：位置 ;：速度

我们假设 a（k）是未知的，并且呈正态分布，均值为 0，标准差为 \sigma_a。根据牛顿运动定律，我们得出结论：x（k） = F x（k-1） + G a（k）

我们假设 a（k）$ 项$G没有控制输入，其中 $$F = [1 \quad Δt;0 \quad 1]$$ $$G = [Δt^2/2;Δt]$$

然后，使用PID控制器生成加速度（$a$），以使用估计的加速度（$\tilde{v}$）来控制机器人的速度（v）。

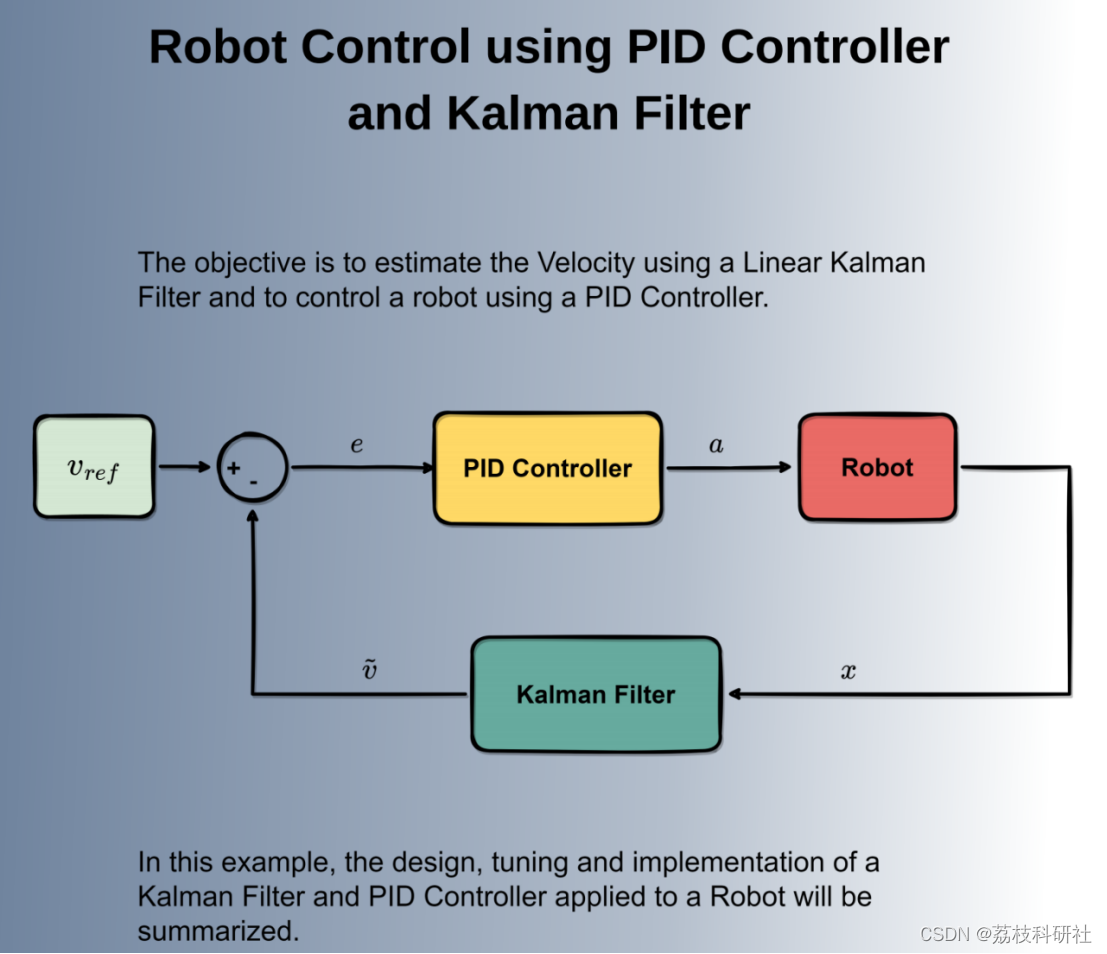
基于PID控制器与卡尔曼滤波器的机器人控制研究

一、PID控制器的基本原理与机器人应用

核心原理
PID控制器通过比例（P）、积分（I）、微分（D）三环节的组合，实现对系统误差的动态调节。其离散位置式公式为：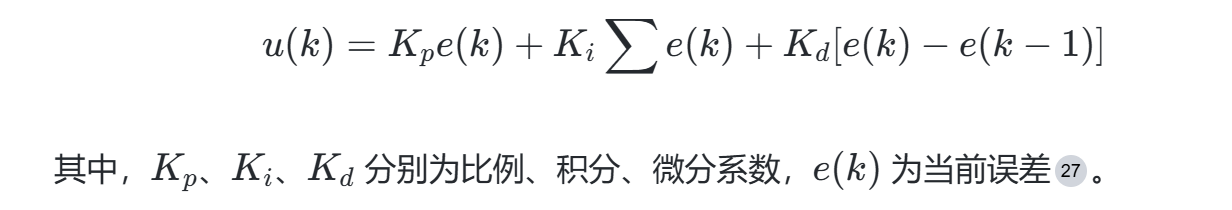
机器人控制中的应用
- 位置与速度控制：通过实时比较目标值与实际值（如编码器反馈），调整电机输入信号，实现精准运动。
- 抗干扰能力：比例环节快速响应误差，积分消除稳态偏差，微分预测误差趋势，适用于动态环境。
- 案例：PUMA560机械臂的轨迹跟踪、自平衡机器人姿态调节。
参数整定方法
- 工程法：临界比例法、反应曲线法。
- 智能优化：遗传算法（GA）通过最小化积分平方误差（ISE）自动优化参数。

二、卡尔曼滤波器的基本原理与机器人应用

核心原理
卡尔曼滤波器通过预测-更新循环实现最优状态估计：
- 预测：基于系统模型预测下一状态及协方差。
- 更新：融合传感器数据，计算卡尔曼增益以修正预测值。
- 扩展卡尔曼滤波（EKF） ：通过一阶泰勒展开处理非线性系统。
机器人控制中的应用
- 传感器融合：融合IMU、GPS、编码器数据，提升位姿估计精度。
- 噪声抑制：滤除加速度计高频噪声与陀螺仪漂移。
- 案例：SLAM中的地图构建、无人机姿态稳定。

三、PID与卡尔曼滤波器的协同控制策略

架构设计
- 分层结构：卡尔曼滤波器作为状态估计层，PID作为控制执行层。
- 数据流：传感器数据→卡尔曼滤波→状态估计→PID计算→执行器输出。
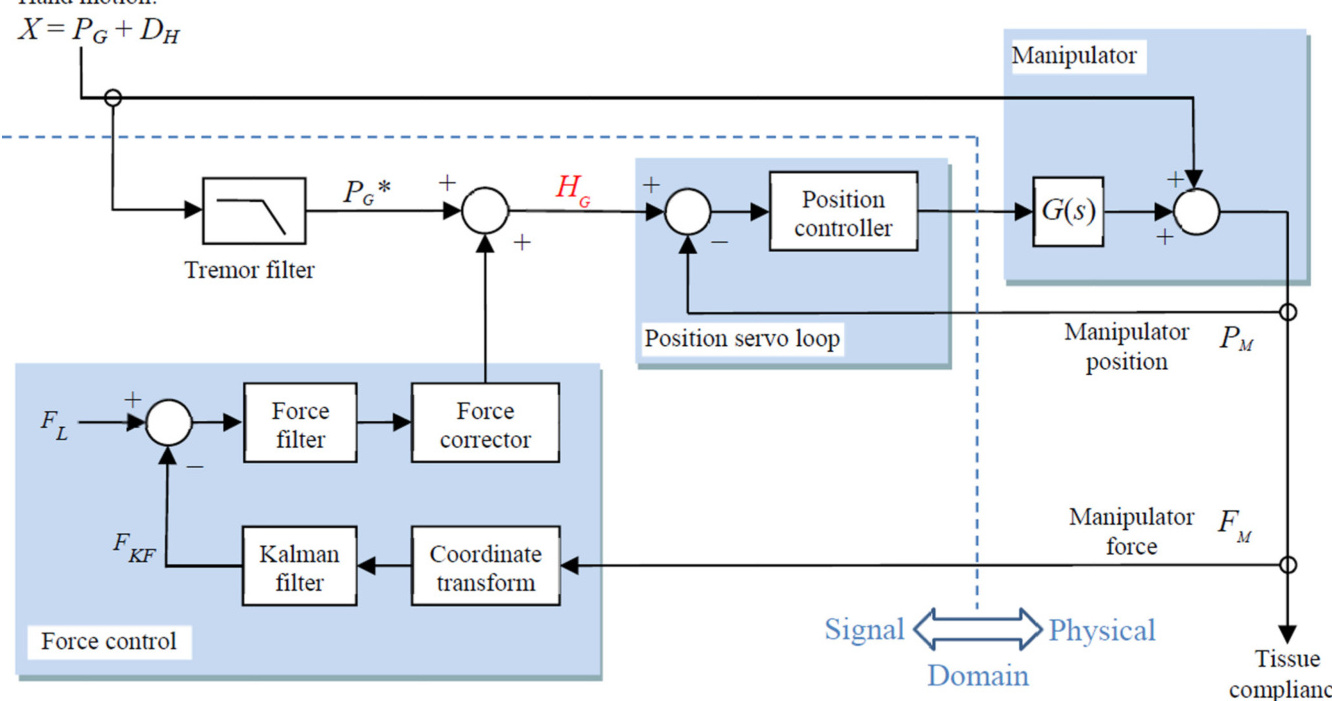
优势分析
- 鲁棒性提升：卡尔曼滤波减少传感器噪声对PID的影响，避免控制振荡。
- 动态适应性：PID参数可基于卡尔曼估计的状态动态调整。
- 案例效果：
  - 在INS/GPS导航系统中，结合PID的卡尔曼滤波器将综合误差（IAE）从60.9降至31.0。
  - 激光充电无人机中，PID-卡尔曼组合优化光束方向，充电效率提升20%。
实现方法
- 嵌入式平台：如Arduino集成MPU6050传感器，通过卡尔曼滤波输出平滑姿态角，PID调节电机PWM。
- 仿真验证：MATLAB/Simulink中对比显示，加入卡尔曼滤波后阶跃响应超调量减少50%。

四、挑战与未来方向

局限性
- 模型依赖：卡尔曼滤波需精确系统模型，非线性场景需EKF或UKF。
- 计算复杂度：嵌入式系统需优化算法实时性。
前沿探索
- 自适应滤波：结合深度学习动态调整卡尔曼参数。
- 多模态控制：PID-卡尔曼与模糊逻辑、强化学习结合。

五、结论

PID控制器与卡尔曼滤波器的结合，通过“状态估计-动态控制”的闭环架构，显著提升了机器人系统的精度与鲁棒性。未来，随着智能算法的融合与硬件算力的提升，该混合控制策略将在自主导航、精密操作等领域发挥更大潜力。

📚2 运行结果

2.1 Estimated vs Real Position

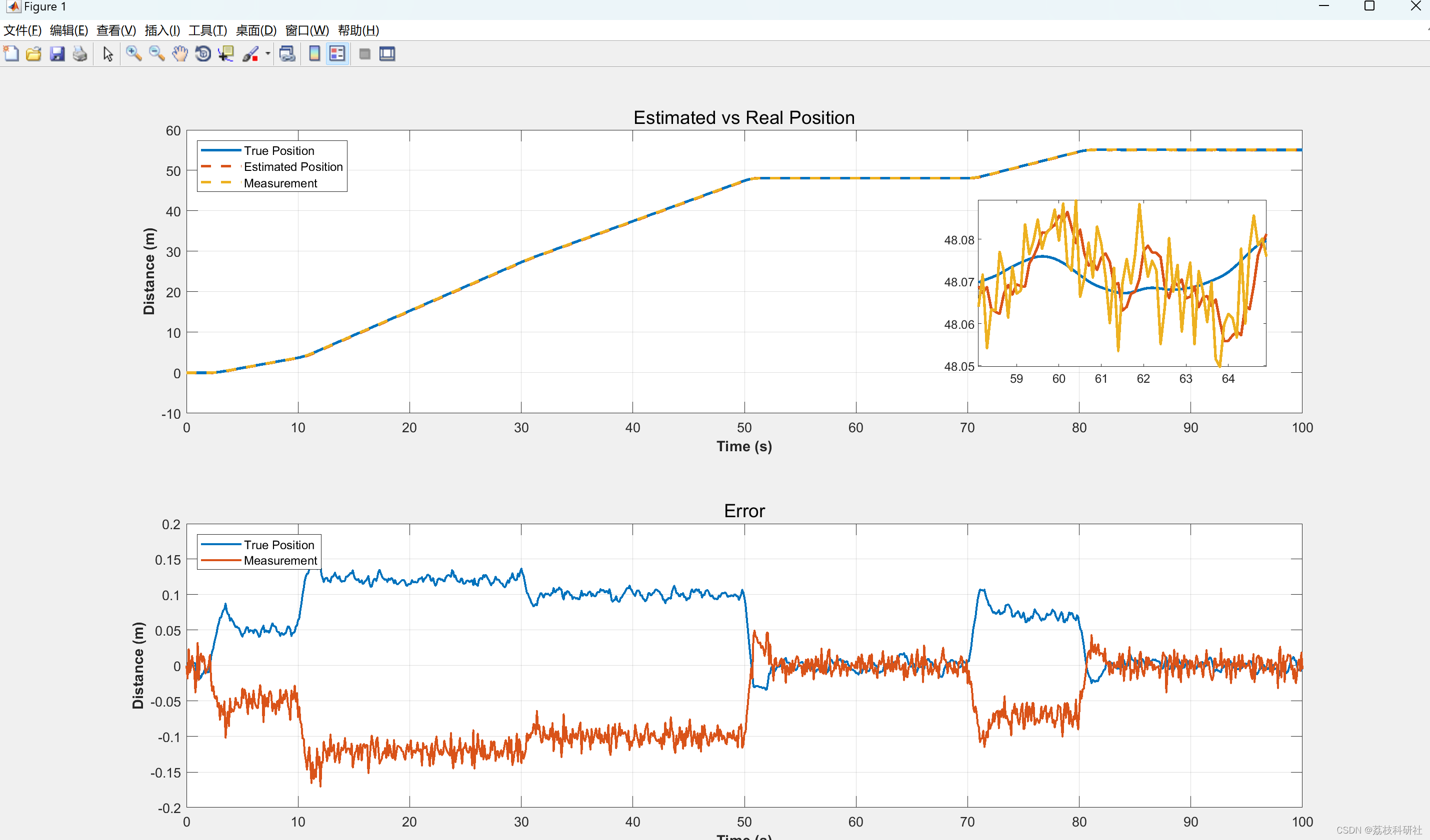
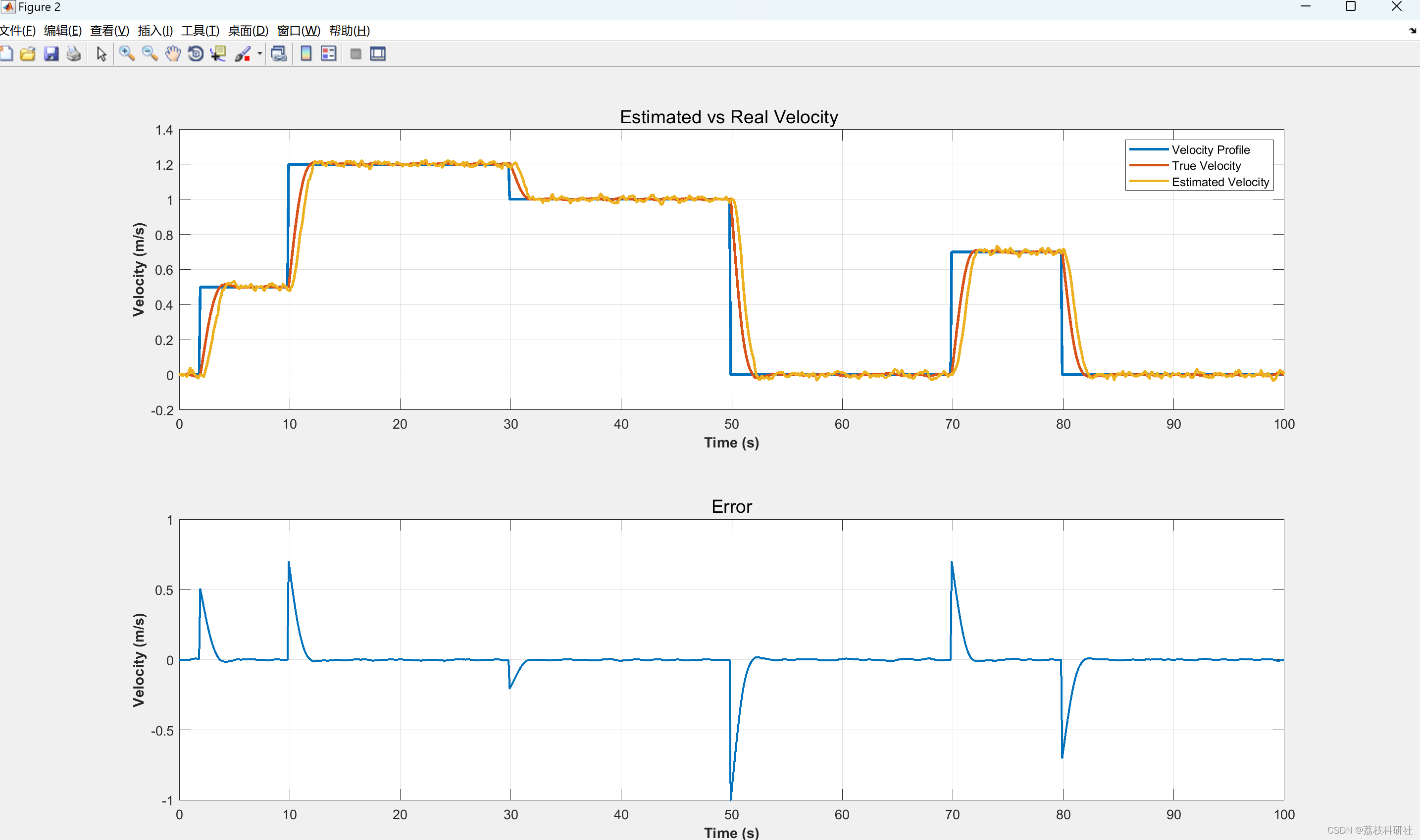
2.2 Estimated vs Real Velocity

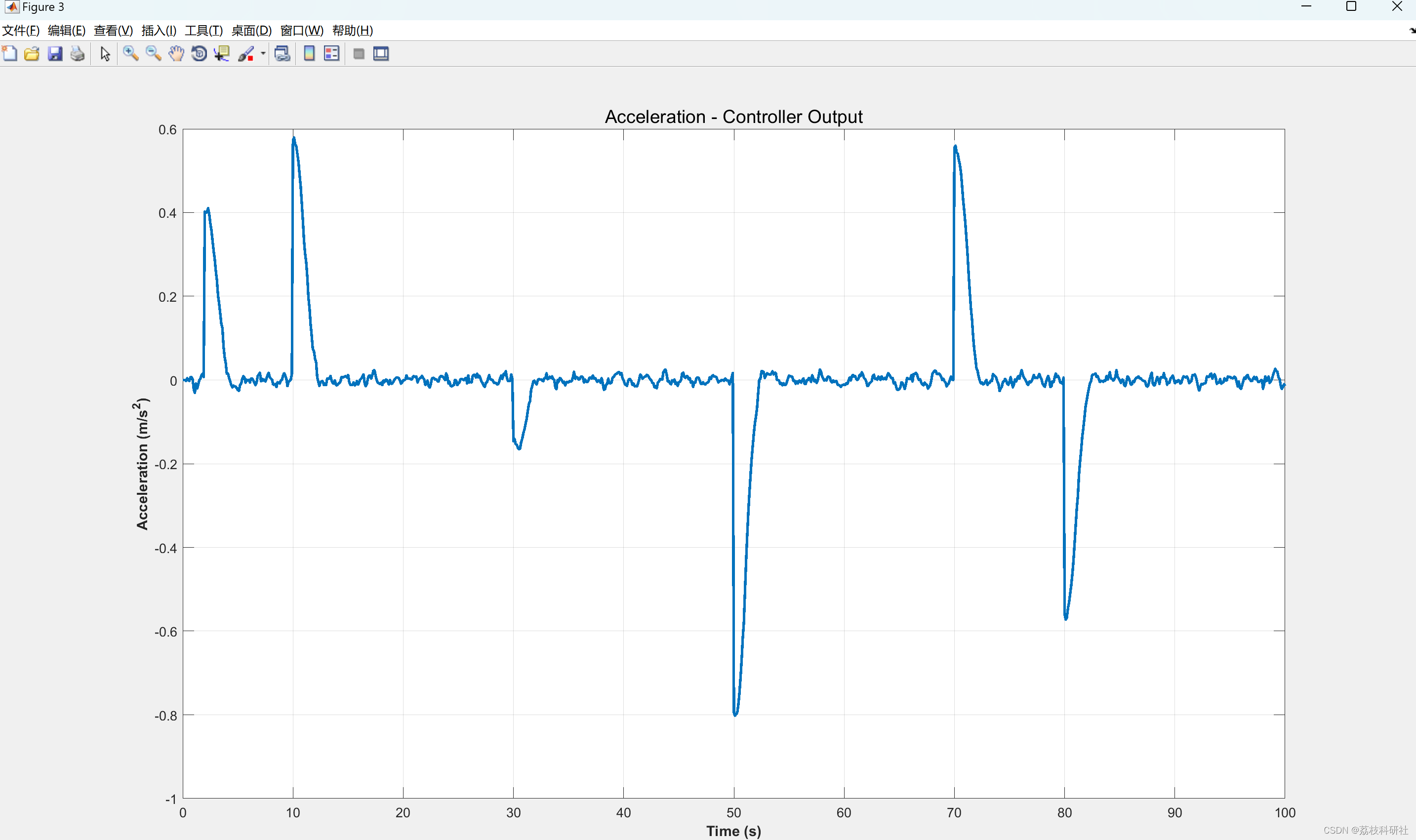
2.3 Acceleration - Controller Output

部分代码：

%% Plot Data
maxfig
subplot(2,1,1)
plot(time,x(1,:),'-',time,x_hat(1,:),'--',time, y,'--','Linewidth',2)
xlabel('Time (s)','fontweight','bold')
ylabel('Distance (m)','fontweight','bold')
grid on
legend('True Position','Estimated Position','Measurement','Location','northwest')
title('Estimated vs Real Position', 'FontSize', 14)
axes('position',[.68 .64 .2 .2])
box on
your_index = 58<time & time<65;
plot(time(your_index),x(1,your_index),time(your_index),x_hat(1,your_index),time(your_index),y(your_index),'Linewidth',2)
axis tight

subplot(2,1,2)
plot(time,x(1,:)-x_hat(1,:),time,x_hat(1,:)-y,'Linewidth',1.5)
legend('True Position','Measurement','Location','northwest')
xlabel('Time (s)','fontweight','bold')
ylabel('Distance (m)','fontweight','bold')
grid on
title('Error', 'FontSize', 14)
saveas(gcf,'Position.png')

maxfig
subplot(2,1,1)
plot(time,Velocity,time,x(2,:),time,x_hat(2,:),'Linewidth',2)
xlabel('Time (s)','fontweight','bold')
ylabel('Velocity (m/s)','fontweight','bold')
legend('Velocity Profile','True Velocity','Estimated Velocity','Location','northeast')
grid on
title('Estimated vs Real Velocity ', 'FontSize', 14)
subplot(2,1,2)
plot(time,Velocity-x(2,:),'Linewidth',1.5)
xlabel('Time (s)','fontweight','bold')
ylabel('Velocity (m/s)','fontweight','bold')
grid on
title('Error', 'FontSize', 14)
saveas(gcf,'Velocity.png')

maxfig
plot(time,a,'Linewidth',2)
xlabel('Time (s)','fontweight','bold')
ylabel('Acceleration (m/s^2)','fontweight','bold')
grid on
title('Acceleration - Controller Output', 'FontSize', 14)
saveas(gcf,'Acceleration.png')

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。(内容仅供参考，以运行结果为准。)

[1]彭道刚,赵晨洋,戚尔江.基于准模型校准卡尔曼滤波的巡检机器人运动系统辨识研究[J].电气传动,2020,50(04):74-80.DOI:10.19457/j.1001-2095.dqcd19286.

[2]赵泽锴,陈增,古依伶,王玲杜玉,彭晓波,冯文博,张明明.基于容积卡尔曼滤波-自适应PID的共轴无人机设计[J].科技创新与应用,2023,13(07):38-41.DOI:10.19981/j.CN23-1581/G3.2023.07.008.