【带宽感知自适应模式分解】铁路轴承故障诊断的带宽感知自适应模式分解（Matlab代码实现）

最新推荐文章于 2025-12-10 21:00:00 发布

原创最新推荐文章于 2025-12-10 21:00:00 发布 · 886 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #人工智能 #算法 #支持向量机

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

铁路轴承故障诊断的带宽感知自适应模式分解研究

带宽感知自适应模式分解（Bandwidth-Aware Adaptive Mode Decomposition，BAAMD）是一种用于信号处理和特征提取的方法。在铁路轴承故障诊断中，BAAMD可以帮助提取出信号中蕴含的有关轴承运行状态和故障特征的信息。

具体来说，铁路轴承在运行过程中会产生振动信号，这些信号包含了轴承的工作状态和可能存在的故障信息。通过应用带宽感知自适应模式分解，可以将振动信号分解成多个不同频率的子信号，每个子信号对应着不同的运行模式或特征。这样一来，就能更好地分析和识别出轴承的运行状态，判断是否存在故障，并进一步进行诊断和预测。

一、研究背景与意义

铁路轴承作为高速列车运行的关键部件，其运行状态直接关系到行车安全。然而，由于铁路轴承工作环境复杂，载荷多变，故障类型多样，传统的故障诊断方法在处理非平稳、非线性信号时存在局限性，难以准确提取故障特征。因此，研究一种高效、准确的铁路轴承故障诊断方法具有重要的理论和实际意义。

带宽感知自适应模式分解（Bandwidth-aware Adaptive Mode Decomposition, BA-AMD）技术为解决此类问题提供了新的思路。该技术通过引入带宽感知机制，在自适应模式分解的过程中更精准地分离出不同频率成分的本征模态，从而有效提取故障特征，提高诊断的准确性和可靠性。

二、BA-AMD技术原理与优势

技术原理：
- BA-AMD在自适应模式分解的基础上，引入带宽感知机制，通过监测信号的带宽变化来动态调整分解过程，从而更准确地分离出不同频率成分的本征模态。
- 该技术能够自适应地处理非平稳、非线性信号，无需预设基函数，根据信号自身的特性进行分解。
技术优势：
- 减少模态混叠：通过引入带宽信息，BA-AMD能够更有效地识别和分离具有相似频率的信号分量，显著减少模态混叠现象，提高分解的纯净度。
- 提高信噪比：在分解过程中，BA-AMD能够更好地将噪声分量从故障特征信号中分离出来，从而提高故障特征的信噪比，为后续的特征提取和故障诊断提供更清晰的数据基础。
- 适应复杂工况：BA-AMD保留了自适应模式分解的优点，能够更好地适应铁路轴承在不同工况下的复杂振动信号，提高诊断的通用性。
- 有效处理非平稳信号：铁路轴承的故障信号往往具有非平稳、非线性的特点，BA-AMD能够有效处理这类信号，从中提取出反映故障状态的关键信息。

三、BA-AMD在铁路轴承故障诊断中的应用流程

信号采集：通过安装在轴承座上的传感器，采集轴承运行过程中的振动信号。
BA-AMD处理：对采集到的原始振动信号进行BA-AMD处理，将其分解为一系列具有不同频率和幅值的本征模态函数（IMF）。
模态分量选择：根据先验知识或统计分析方法，从分解得到的IMF中选择与故障相关的模态分量。这些模态分量往往包含有故障冲击的周期性信息。
特征提取：对选定的模态分量进行进一步的特征提取，例如包络解调分析、希尔伯特变换等，以显化故障特征频率。
故障诊断：将提取到的故障特征与已知的故障模式进行比对，从而判断轴承的故障类型和程度。这可以借助机器学习算法，如支持向量机（SVM）、神经网络等。

四、实际应用案例与效果分析

在实际工程应用中，BA-AMD技术已经成功应用于铁路轴承的故障诊断。例如，某铁路局采用BA-AMD技术对高速列车的轴承进行故障诊断，通过采集轴承振动信号并进行BA-AMD处理，成功提取出了轴承故障的特征频率，并准确诊断出了轴承的故障类型和程度。与传统的故障诊断方法相比，BA-AMD技术显著提高了诊断的准确性和可靠性，为铁路轴承的维修和更换提供了重要的参考信息。

五、面临的挑战与未来展望

面临的挑战：
- 算法效率：BA-AMD算法的实现相对复杂，计算量较大，尤其对于实时在线诊断系统而言，其计算效率是一个需要关注的问题。
- 参数优化：BA-AMD算法中可能存在一些需要优化的参数，这些参数的选择会影响分解结果的准确性。如何根据实际信号特性进行自适应参数优化是未来的研究方向。
- 多源信息融合：单一的振动信号可能无法全面反映轴承的故障状态。结合温度、转速、载荷等多源信息进行融合诊断，将进一步提高诊断的准确性和可靠性。
- 大数据处理：铁路轴承监测系统会产生海量的振动数据，如何高效存储、管理和处理这些数据，并从中挖掘出有价值的故障信息，是大数据时代背景下亟待解决的问题。
未来展望：
- 深度学习结合：随着深度学习技术的发展，将其与BA-AMD相结合，实现故障特征的自动学习和诊断，有望进一步提升诊断的智能化水平。
- 算法优化与改进：针对BA-AMD算法存在的计算效率低和参数优化难等问题，未来可以研究更高效的算法实现方式和自适应参数优化方法。
- 多源信息融合诊断：结合温度、转速、载荷等多源信息进行融合诊断，提高诊断的准确性和可靠性。
- 大数据处理技术应用：利用大数据处理技术对海量的振动数据进行高效存储、管理和处理，挖掘出有价值的故障信息。

📚2 运行结果

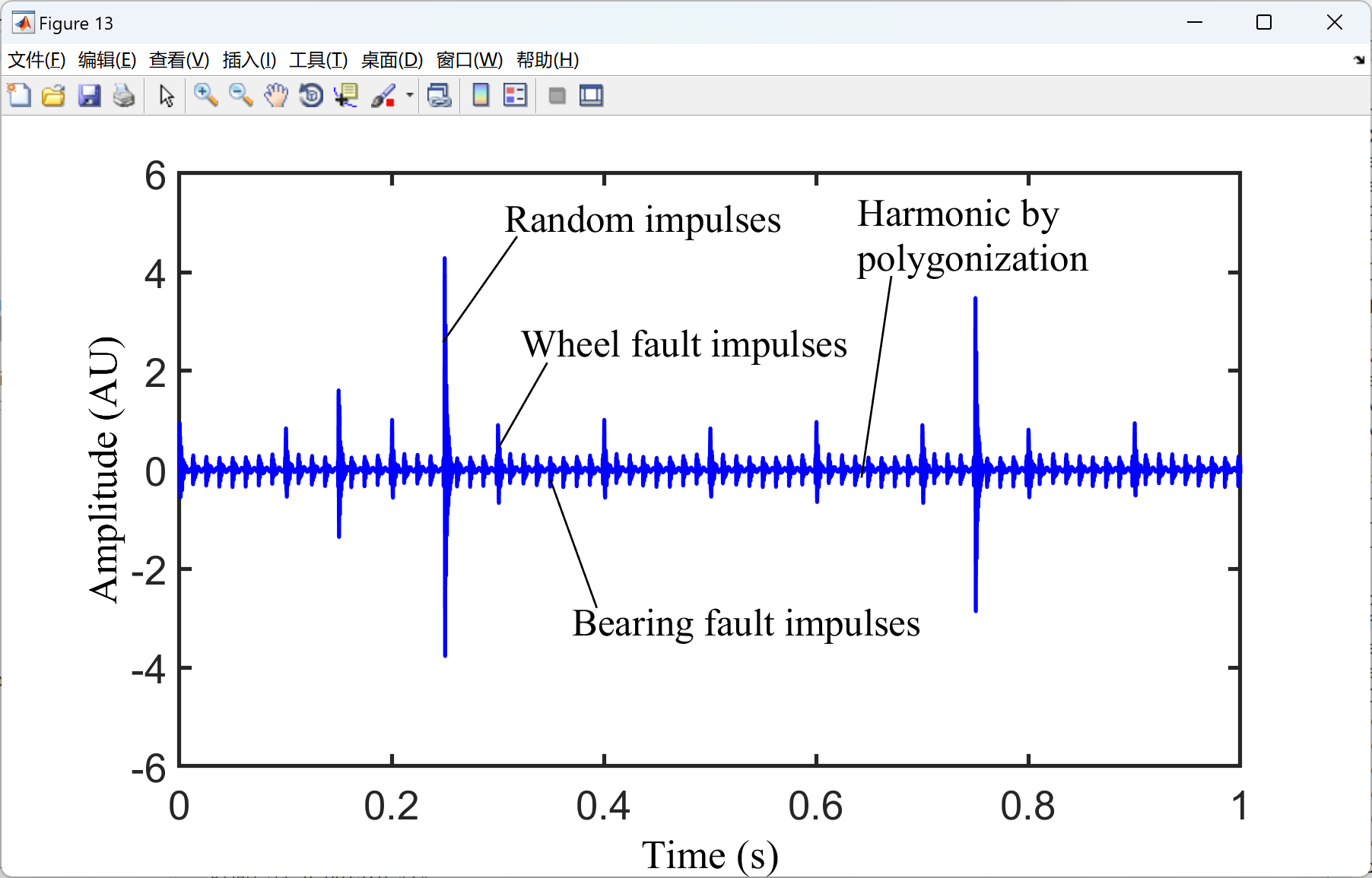
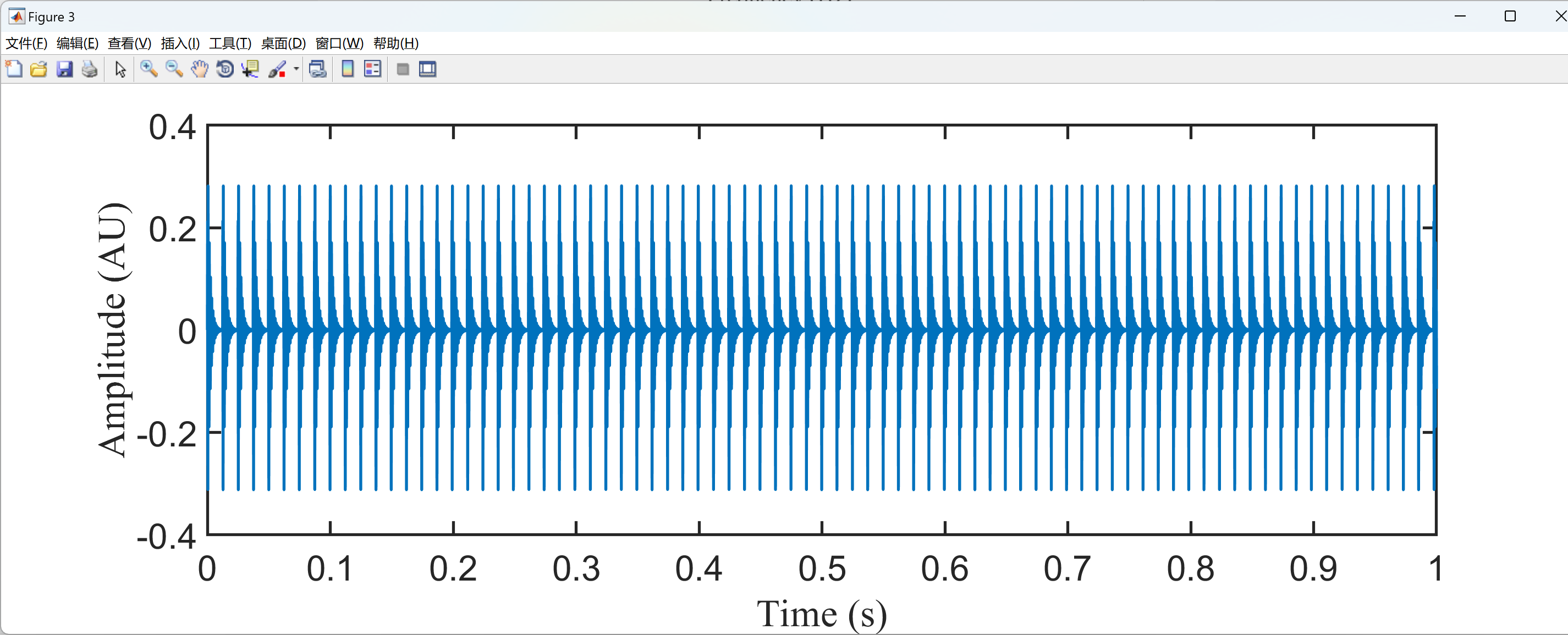
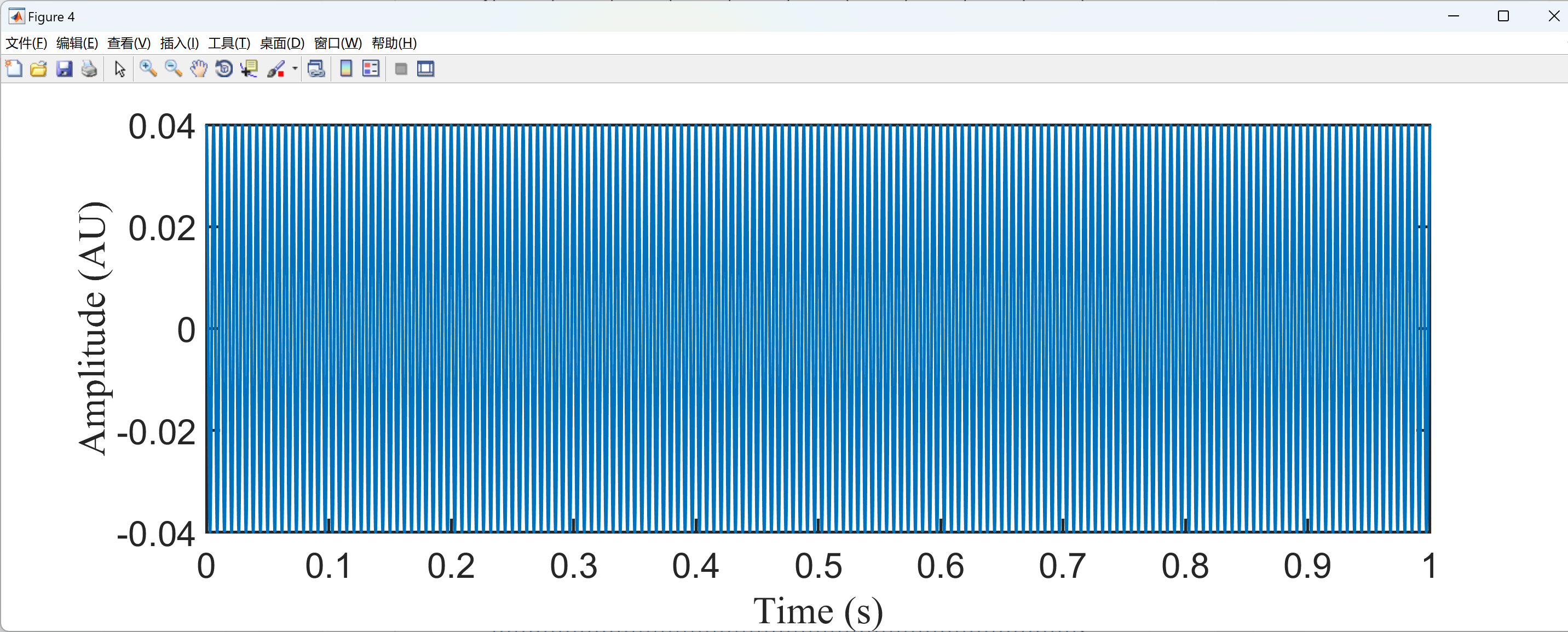
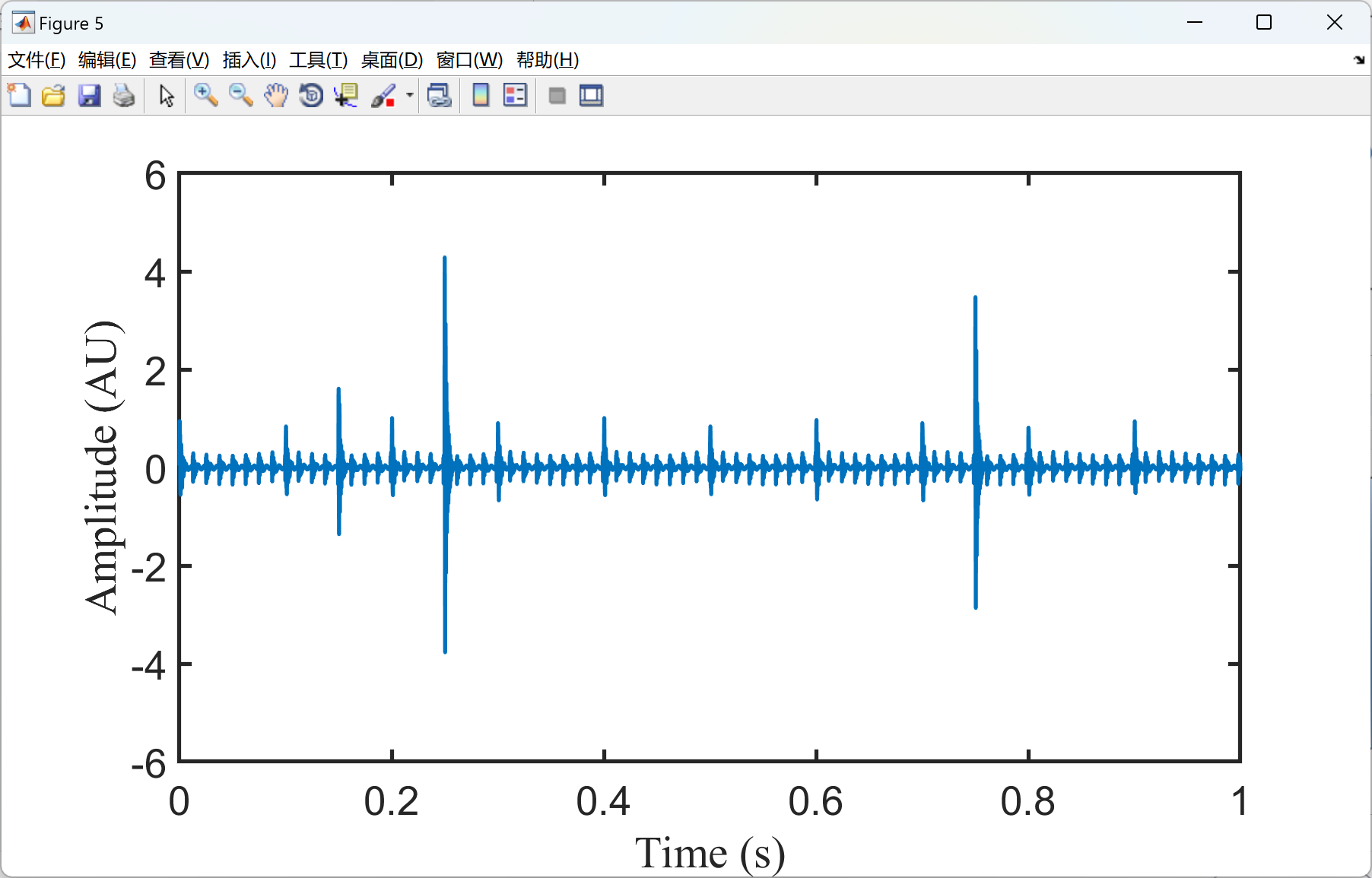
部分代码：

figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
plot(t,Sig2,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
plot(t,Sig1,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
plot(t,Sig3,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
plot(t,Sig4,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);

figure
set(gcf,'Position',[20 100 900 500]);
set(gcf,'Color','w');
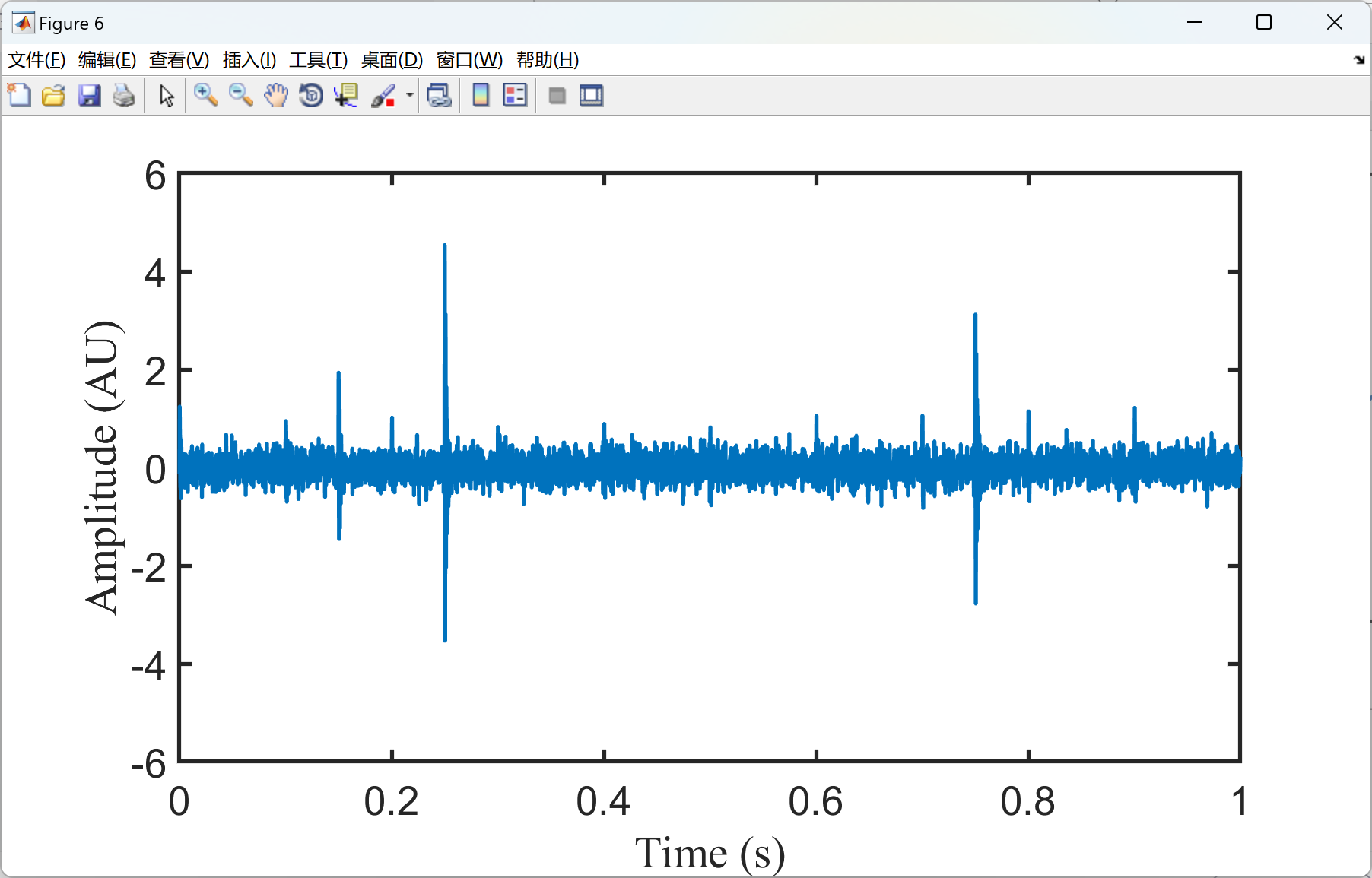
plot(t,Sig,'linewidth',2);
xlabel('Time (s)','FontSize',20,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);
axis([0 1 -6 6])

figure
set(gcf,'Position',[20 100 900 500]);
set(gcf,'Color','w');
plot(t,Sign,'linewidth',2);
xlabel('Time (s)','FontSize',20,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);
axis([0 1 -6 6])
%%
offset = 0.01;
cutpfreq = 0.0015;

round(2*length(Sig)*cutpfreq)

tic
[Spec,Weigt,Spec_trend,WeSpec_trend,sortInter] = Spectrendgene(Sign,SampFreq,offset,cutpfreq);
beta = 1e-10;
tol = 1e-7;
ce = 0.3;
[compset IFset IAset] = BAACMD(Sign,SampFreq,beta,tol,ce,offset,cutpfreq);
toc

Freqbin = linspace(0,SampFreq/2,length(Spec));
[peakset,indexp] = findpeaks(-Spec_trend);
figure
set(gcf,'Position',[20 100 900 500]);
set(gcf,'Color','w');
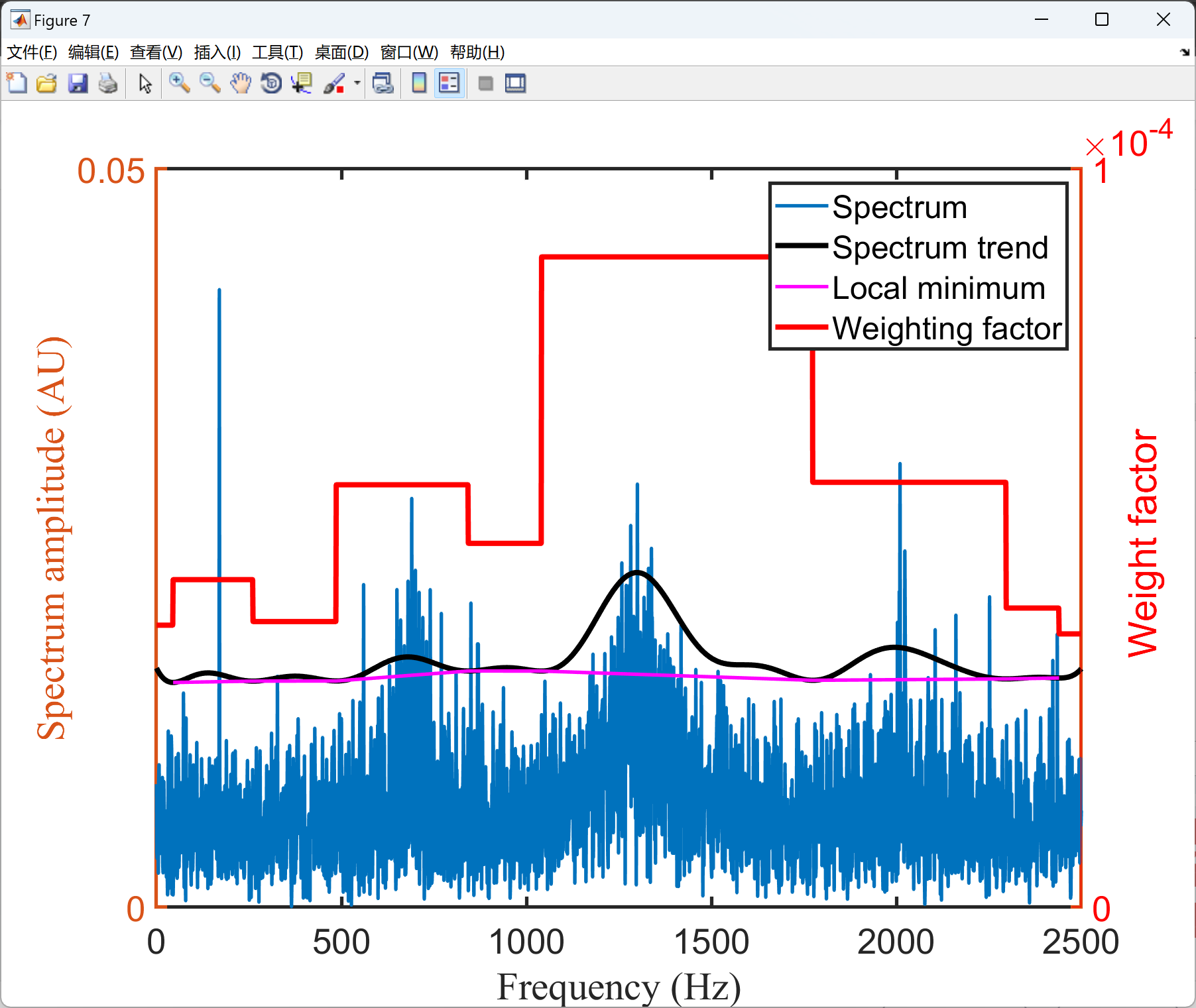
plot(Freqbin,Spec,'linewidth',2);
hold on
plot(Freqbin,Spec_trend,'k','linewidth',3);
ylabel('Amplitude (AU)','FontSize',18,'FontName','Times New Roman');
axis([0 2500 0 1.1*max(Spec)])
hold on
[AX,H1,H2] =plotyy(Freqbin(indexp),-peakset,Freqbin,Weigt,@plot);% 禄帽脠隆脳酶卤锚脰谩隆垄脥录脧帽戮盲卤煤
set(get(AX(1),'ylabel'),'string', 'Spectrum amplitude (AU)','fontsize',20);
set(get(AX(2),'ylabel'),'string', 'Weight factor ','fontsize',20);
set(AX(2),'Fontsize',20)
set(H1,'linewidth',2);
set(H2,'linewidth',3);
set(H2,'color','r')
set(H1,'color','m')
set(AX(2),'YColor', [1 0 0]);
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',20,'FontName','Times New Roman');
legend('Spectrum','Spectrum trend','Local minimum','Weighting factor')
set(gca,'FontSize',20)
set(gca,'linewidth',2);

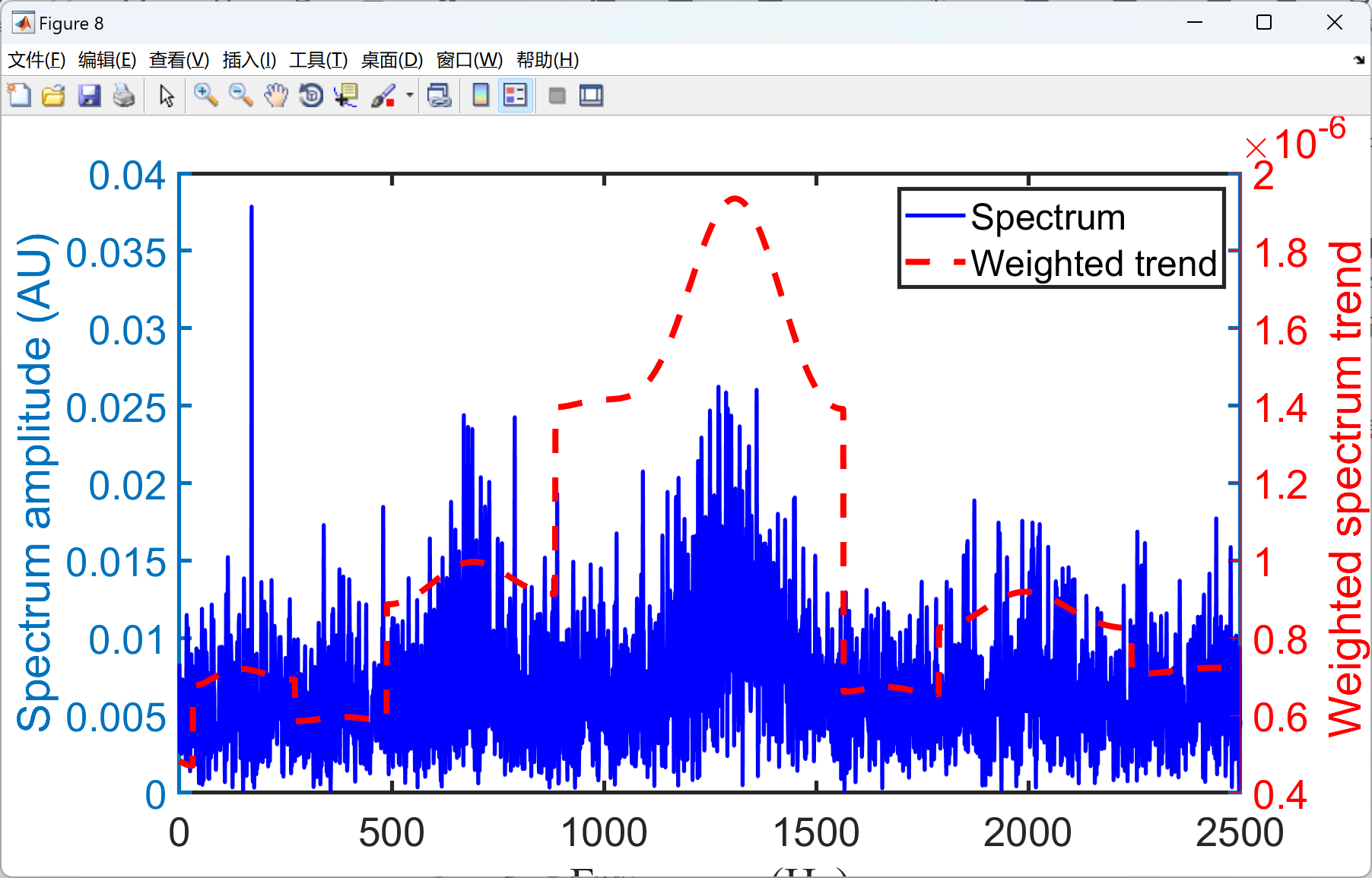
figure
set(gcf,'Position',[20 100 900 500]);
set(gcf,'Color','w');
[AX,H1,H2] =plotyy(Freqbin,Spec,Freqbin,WeSpec_trend,@plot);
set(get(AX(1),'ylabel'),'string', 'Spectrum amplitude (AU)','fontsize',20);
set(get(AX(2),'ylabel'),'string', 'Weighted spectrum trend ','fontsize',20);
set(AX(2),'Fontsize',20)
set(H1,'Linestyle','-','linewidth',2);
set(H2,'Linestyle','--','linewidth',3);
set(H1,'color','b')
set(H2,'color','r')
set(AX(2),'YColor', [1 0 0]);
legend('Spectrum','Weighted trend')
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);

Specpset = zeros(size(compset,1),length(Freqbin));

for cpnum = 1:size(compset,1)
Specp1 = (2*abs(fft(compset(cpnum,:)))/length(compset(cpnum,:)));
Specpset(cpnum,:) = Specp1(1:length(Freqbin));
end

figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
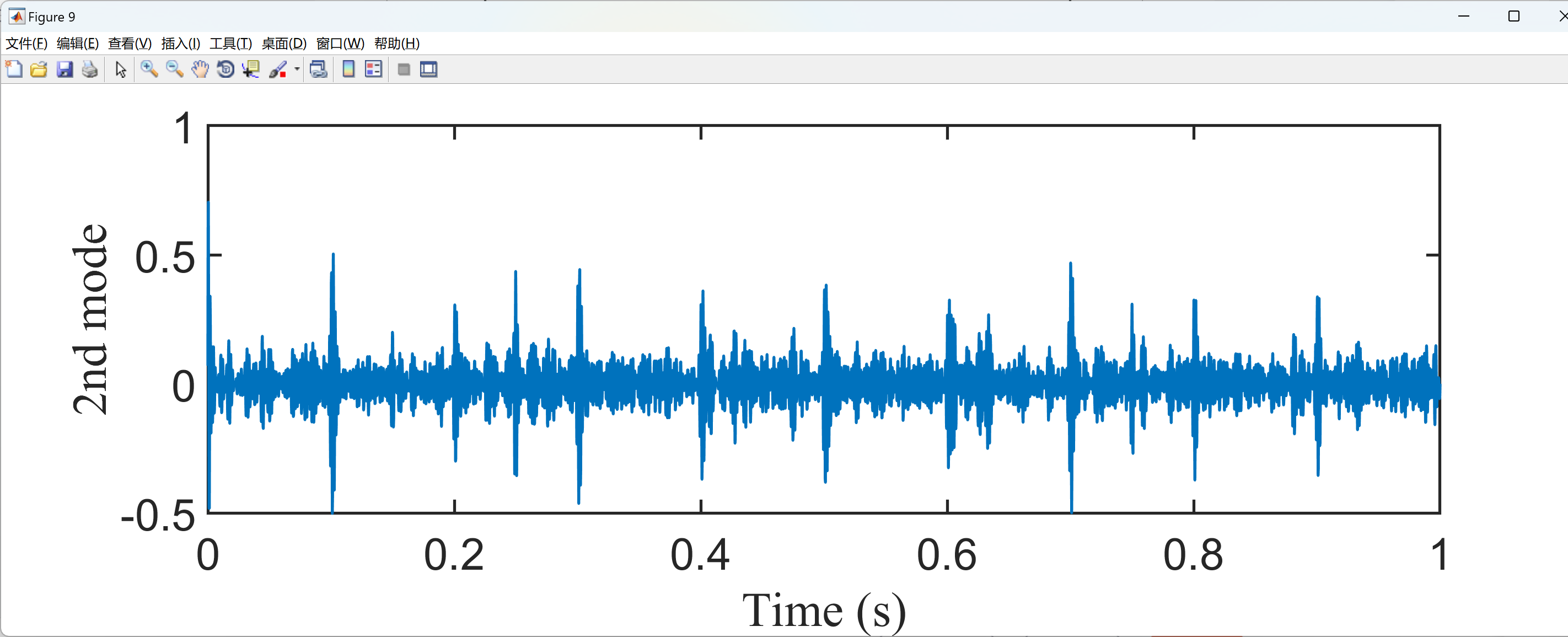
plot(t,compset(2,:),'linewidth',2);
xlabel('Time (s)','FontSize',30,'FontName','Times New Roman');
ylabel('2nd mode','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);
% axis([0 1 -0.4 0.4])

figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
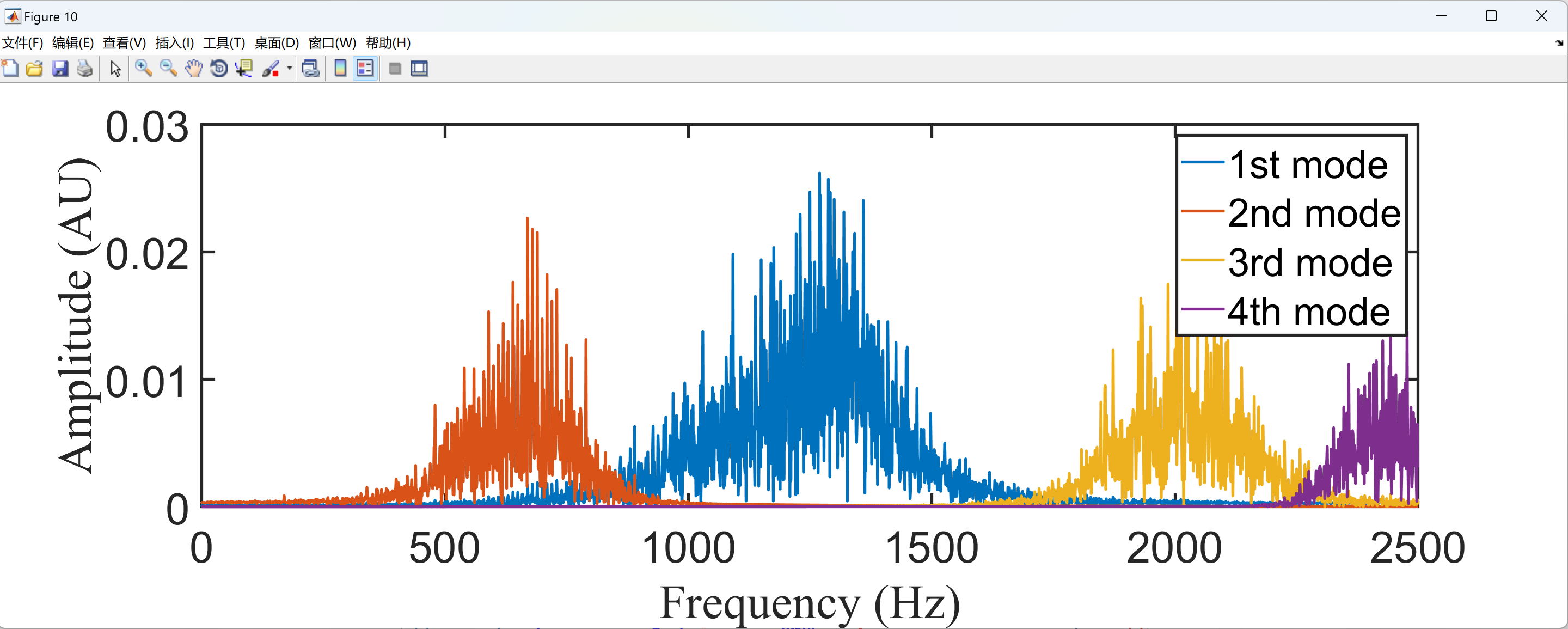
plot(Freqbin,Specpset,'linewidth',2);
ylabel('Amplitude (AU)','FontSize',30,'FontName','Times New Roman');
legend('1st mode','2nd mode','3rd mode','4th mode')
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);

[IFcp1 IAcp1]= IFIAextrc(compset(2,:),SampFreq);
SpeIFcp1 = (2*abs(fft(IAcp1 - mean(IAcp1)))/length(IAcp1)); % envelope spectrum
SpeIFcp1 = SpeIFcp1(1:length(Freqbin));
figure
set(gcf,'Position',[20 100 1500 500]);
set(gcf,'Color','w');
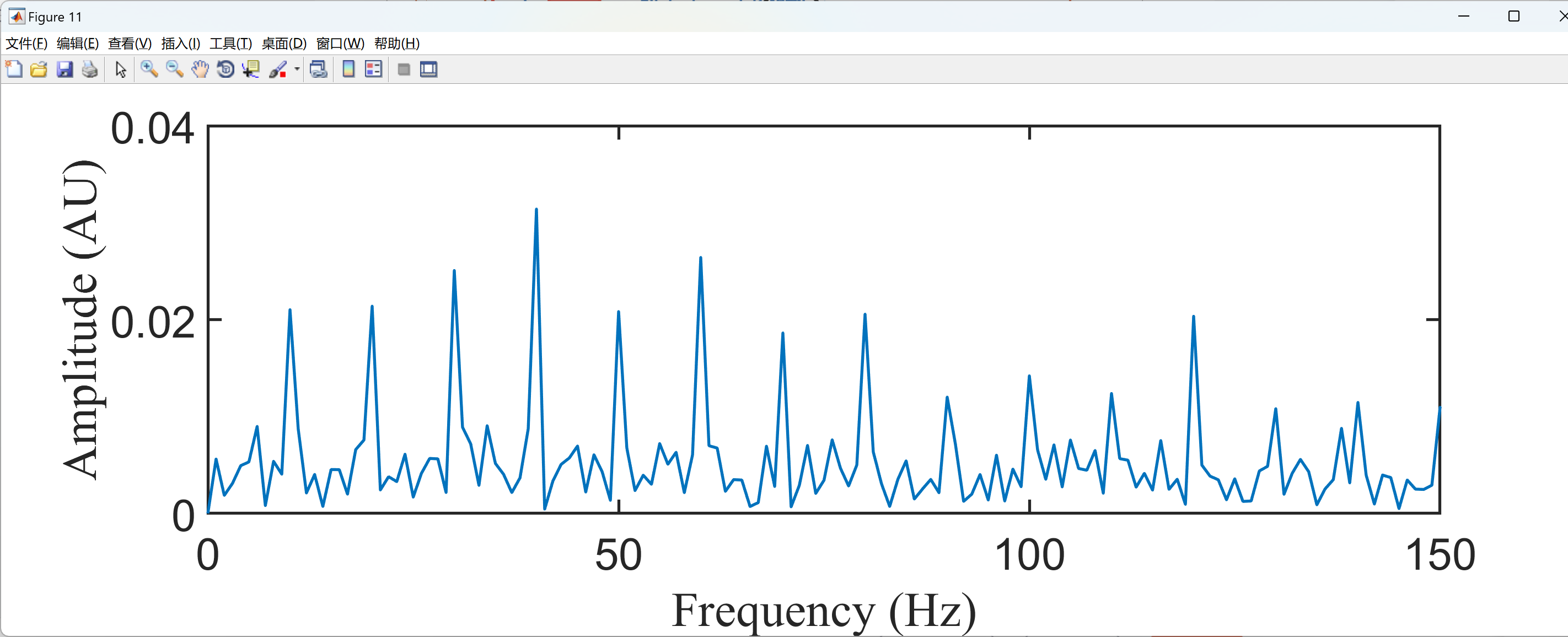
plot(Freqbin,SpeIFcp1,'linewidth',2);
ylabel('Amplitude (AU)','FontSize',30,'FontName','Times New Roman');
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);
axis([0 150 0 0.04])

GN1 = GN_SE(compset(1,:))
GN1 = GN_SE(compset(2,:))
GN1 = GN_SE(compset(3,:))
GN1 = GN_SE(compset(4,:))