【无人机3D路径规划】基于改进蝙蝠优化算法的无人机3D路径规划研究（Matlab代码实现）

  💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

无人机的3D路径规划是一项复杂而关键的任务，尤其是在动态环境中。改进蝙蝠优化算法是一种启发式算法，可以用于优化路径规划问题。在这项研究中，你将探索如何将改进的蝙蝠优化算法应用于无人机的3D路径规划中。

基于改进蝙蝠优化算法的无人机3D路径规划研究

摘要

随着无人机技术的快速发展，其在军事侦察、物流运输、灾害救援等领域的应用日益广泛。无人机路径规划作为关键技术之一，直接影响无人机的作业效率和安全性。传统路径规划方法在复杂三维环境下存在计算量大、易陷入局部最优等问题。本文提出了一种基于改进蝙蝠优化算法（Improved Bat Algorithm, IBA）的无人机3D路径规划方法，通过引入自适应惯性权重和Levy飞行策略，增强了算法的全局搜索能力和收敛速度。仿真实验表明，IBA算法在路径长度、平滑度和避障能力方面均优于传统算法，能够为无人机在复杂环境下提供安全、高效的路径规划方案。

关键词

无人机；3D路径规划；改进蝙蝠优化算法；自适应惯性权重；Levy飞行

1. 引言

无人机（Unmanned Aerial Vehicle, UAV）作为一种新型航空平台，以其成本低廉、操作灵活、适应性强等优点，在多个领域展现出巨大潜力。然而，要充分发挥无人机的性能优势，精确、高效的路径规划技术是关键环节之一。无人机路径规划旨在复杂三维环境中，为无人机规划一条从起始点到目标点，满足动力学约束、避开障碍物、优化性能指标（如路径长度、飞行时间、燃料消耗）的最优或次优飞行轨迹。

传统路径规划方法包括图搜索算法（如Dijkstra算法、A*算法）、采样算法（如RRT系列算法）和智能优化算法（如遗传算法、粒子群算法、蚁群算法）。但这些方法在处理高维复杂环境时存在计算复杂度高、随机性强导致路径不平滑、收敛速度慢、易陷入局部最优等问题。

蝙蝠优化算法（Bat Algorithm, BA）是一种基于微蝙蝠回声定位行为的仿生智能优化算法，具有概念简单、易于实现、全局搜索能力强等优点。然而，标准BA算法在解决复杂优化问题时存在收敛速度慢、局部搜索能力不足、后期多样性丧失等问题。针对这些问题，本文提出了一种改进蝙蝠优化算法（IBA），通过引入自适应惯性权重和Levy飞行策略，增强了算法的全局搜索能力和收敛速度，并有效避免了早熟收敛。

2. 蝙蝠优化算法原理与改进

2.1 标准蝙蝠算法（BA）

蝙蝠算法模拟蝙蝠利用声纳进行捕食的行为，每只蝙蝠代表一个潜在解，通过调整频率、速度和位置来搜索最优解。算法流程如下：

1. 初始化：生成一组随机蝙蝠种群，定义频率、速度、位置、响度和脉冲率等参数。
2. 全局搜索：蝙蝠根据随机生成的频率在解空间中探索新位置。
3. 局部搜索：围绕当前最优解附近进行细致搜索，更新位置。
4. 迭代更新：通过调整频率和响度，评估路径优劣，更新蝙蝠位置。
5. 终止条件：达到预定迭代次数或目标函数值满足要求时终止。

2.2 改进蝙蝠算法（IBA）

针对标准BA算法的不足，本文提出以下改进策略：

2.2.1 自适应惯性权重

惯性权重是平衡全局搜索和局部开发能力的重要参数。IBA算法在速度更新公式中引入自适应惯性权重，使得算法在不同阶段具有不同的搜索策略：

• 初期：赋予较大惯性权重，增强全局探索能力。
• 后期：减小惯性权重，加速局部收敛。

改进后的速度更新公式为：

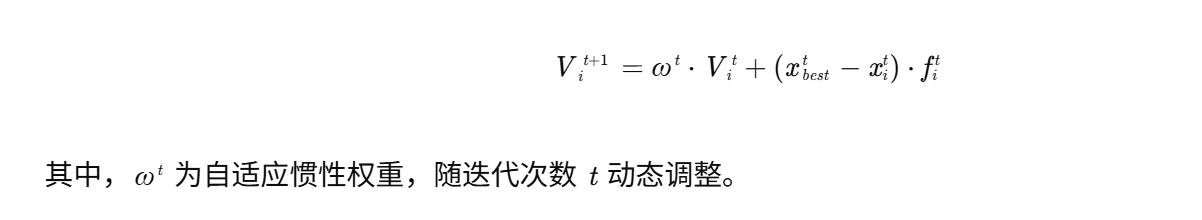
2.2.2 Levy飞行策略

Levy飞行是一种随机游走模式，其步长服从Levy分布，具有长尾特性，能够增强算法的随机性和跳出局部最优的能力。IBA算法在局部搜索阶段引入Levy飞行策略，通过模拟Levy随机游走生成新解，提高全局搜索能力。

Levy飞行步长 Δx 的计算公式为：

3. 基于IBA的无人机3D路径规划模型构建

3.1 三维环境建模

采用三维栅格法对无人机飞行环境进行建模，将连续三维空间离散化为立方体栅格单元。每个栅格单元标记为“可行”或“不可行”，“不可行”栅格代表障碍物或威胁区域，无人机不允许进入。

3.2 目标函数设定

以路径长度最短、飞行能耗最小、避开障碍物风险最高为目标，构建多目标优化函数：

3.3 IBA算法流程

基于IBA的无人机3D路径规划算法流程如下：

1. 初始化：生成蝙蝠种群，定义参数（频率、速度、位置、响度、脉冲率）。
2. 评估适应度：根据目标函数计算每只蝙蝠的适应度值。
3. 全局搜索：蝙蝠根据随机生成的频率在解空间中探索新位置。
4. 局部搜索：引入Levy飞行策略，围绕当前最优解附近进行细致搜索。
5. 自适应惯性权重调整：根据迭代次数动态调整惯性权重。
6. 更新蝙蝠位置：根据适应度值更新蝙蝠位置，保留最优解。
7. 终止条件：达到预定迭代次数或目标函数值满足要求时终止，输出最优路径。

4. 仿真实验与结果分析

4.1 实验设置

• 环境模型：构建包含多个障碍物的三维栅格环境，起点坐标为(0,0,100)，终点坐标为(100,100,100)。
• 算法参数：蝙蝠种群规模为50，最大迭代次数为200，惯性权重初始值为0.9，最终值为0.4。
• 对比算法：标准蝙蝠算法（BA）、遗传算法（GA）。

4.2 实验结果

仿真实验结果表明，IBA算法在路径规划性能上显著优于BA和GA算法：

• 路径长度：IBA算法规划的路径长度比BA短36.56%，比GA短27.16%。
• 收敛速度：IBA算法的收敛时间比BA少49.71%，比GA少60.09%。
• 避障能力：IBA算法能够更有效地避开障碍物，规划出更安全的飞行路径。

4.3 结果分析

IBA算法通过引入自适应惯性权重和Levy飞行策略，有效平衡了全局搜索和局部开发能力，避免了早熟收敛，提高了算法的收敛速度和寻优精度。仿真实验验证了IBA算法在无人机3D路径规划中的优越性和鲁棒性。

5. 结论与展望

本文提出了一种基于改进蝙蝠优化算法（IBA）的无人机3D路径规划方法，通过引入自适应惯性权重和Levy飞行策略，增强了算法的全局搜索能力和收敛速度。仿真实验表明，IBA算法在路径长度、平滑度和避障能力方面均优于传统算法，能够为无人机在复杂环境下提供安全、高效的路径规划方案。

未来研究可进一步优化IBA算法的参数设置和改进策略，提高算法的性能和适应性。同时，考虑将更多实际因素（如天气变化、无人机姿态调整、动态障碍物）纳入路径规划模型，增强模型的实用性和鲁棒性。此外，探索IBA算法与其他智能算法或传感器技术相结合，实现更智能、高效的无人机路径规划，推动无人机技术的广泛应用和发展。

📚2 运行结果

部分代码：

function [ f1 ] = NSGA2_fitness1( dna)
%NSGA2_FITNESS1 Summary of this function goes here
%本函数计算航路长度代价
dnanum=size(dna,1);          %种群数目
dnalength=size(dna,2)-1;     %有几段？相当于种群中的个体为点，点与点之间依次相连有多少条线段，因此要减1
f1=zeros(dnanum,1);          %每段对应的航路长度代价
for i=1:1:dnanum
    f1(i,1)=0;
    for j=1:1:dnalength
        d(1)=(dna(i,j+1,1)-dna(i,j,1))*10;
        d(2)=(dna(i,j+1,2)-dna(i,j,2))*10;  % *10是因为每小段又划分为10格？
        d(3)=dna(i,j+1,3)-dna(i,j,3);
        d=d.^2;
        f1(i,1)=f1(i,1)+sqrt(d(1)+d(2)+d(3));
        %i个体数目
    end
end

%   Detailed explanation goes here
 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]王广生,孙祎峥,孙海军,等.内河船舶尾气监测的多无人机路径规划研究[J].港口航道与近海工程,2024,61(01):93-98.DOI:10.16403/j.cnki.ggjs20240118.

[2]卢颖,庞黎晨,陈雨思,等.一种面向城市战的无人机路径规划群智能算法[J].兵工学报,2023,44(S2):146-156.

🌈4 Matlab代码实现