💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
基于Wasserstein距离的两阶段分布鲁棒优化模型
在不确定性和复杂性日益增加的背景下,传统的优化方法在处理实际问题时面临巨大挑战。分布鲁棒优化(Distributionally Robust Optimization, DRO)作为一种新兴的优化方法,能够在数据分布未知或存在不确定性的情况下进行决策,增强了决策的稳健性。而基于Wasserstein距离的DRO模型在处理不确定性和优化问题方面表现出强大的能力,因此成为当前研究的热点。
基于Wasserstein距离的分布鲁棒优化
Wasserstein距离,也称为地球移动距离,是衡量两个概率分布之间差异的一种方法。它通过寻找最小化将概率质量从一个分布转移到另一个分布所需的“代价”来工作。在分布鲁棒优化中使用Wasserstein距离可以更好地处理有限样本的情况,提供对不确定性的定量度量,同时也使得优化问题更易于重构和求解。
两阶段分布鲁棒模型
两阶段分布鲁棒优化模型是一种考虑决策过程的分阶段优化方法。在第一阶段,决策者需要在不确定性的情况下做出初步决策;在第二阶段,当不确定性实现后,决策者再根据实际情况进行调整。这种模型能够更真实地反映实际决策过程,提高决策的鲁棒性和适应性。
对偶转化
对偶转化是优化理论中的一种重要方法,它通过将原问题转化为对偶问题来求解。在基于Wasserstein距离的两阶段分布鲁棒优化模型中,对偶转化可以帮助我们更好地处理不确定性,将复杂的原始问题转化为更易求解的对偶问题。通过对偶问题的求解,我们可以得到原问题的最优解或近似最优解。
线性决策
线性决策是指在决策过程中,决策者根据线性关系进行决策。在基于Wasserstein距离的两阶段分布鲁棒优化模型中,线性决策方法可以帮助我们简化决策过程,提高决策效率。同时,线性决策方法也便于我们进行敏感性分析和优化调整。
一、分布鲁棒优化的核心思想与Wasserstein距离
分布鲁棒优化(DRO)旨在通过构建概率分布的模糊集(Ambiguity set)来处理不确定性,其核心思想是寻找在最坏概率分布下仍能保持性能的鲁棒解。与传统的随机优化和鲁棒优化相比,DRO结合了两者的优势:既不需要精确的概率分布,又能通过数据驱动降低保守性。
Wasserstein距离的核心作用:
-
定义与性质:Wasserstein距离(又称推土机距离)衡量两个概率分布之间的最小运输成本。对于经验分布PN和真实分布Q,其定义为:

二、两阶段分布鲁棒模型的数学框架
两阶段DRO模型将决策分为 第一阶段(预决策) 和 第二阶段(调整决策) ,以应对不确定性参数的动态性。其一般形式为:

关键特征:
- 保守性控制:通过调节Wasserstein半径ϵϵ平衡鲁棒性与经济性。较大的ϵϵ覆盖更广泛的不确定性,但可能增加成本。
- 数据驱动性:基于历史数据构建经验分布,适用于小样本或非参数化场景。
- 计算可处理性:通过对偶原理和凸优化技术,将无限维分布问题转化为有限维规划。
三、对偶转化与线性决策规则的实现
1. 对偶转化
两阶段模型的复杂性在于内层的双层优化结构(max-min)。通过引入拉格朗日对偶性,可将内层问题转化为单层优化:
2. 线性决策规则(LDR)
为降低第二阶段决策的计算复杂度,常采用仿射决策规则:

四、现有挑战与改进方向
1. 计算复杂度
- 维度诅咒:高维系统(如大规模IES)的模型求解需借助分解算法或近似方法(如场景削减技术)。
- 机会约束处理:基于Wasserstein模糊集的机会约束模型仍缺乏高效求解工具。
2. 参数选择与保守性平衡
- 半径ϵϵ调整:需结合统计学习或贝叶斯方法动态优化半径,避免人工调参的局限性。
- 数据驱动改进:利用深度学习构建模糊集,融合数据几何特征(如梯度流方法)提升泛化能力。
3. 多能源系统协同
- 动态特性建模:考虑热力/天然气系统的传输延时与损耗,增强模型精细化。
- 多目标优化:引入环保指标(如碳排放)与经济效益的权衡,扩展Pareto前沿分析。
五、总结与展望
基于Wasserstein距离的两阶段DRO在电力、能源等领域展现了强大的应用潜力,但其进一步发展需结合以下方向:
- 算法创新:开发高效求解器(如混合整数线性规划加速算法)。
- 跨学科融合:结合机器学习与统计学习,构建自适应模糊集。
- 实际系统验证:在复杂工业场景(如高海拔铁路供电系统)中验证模型鲁棒性。
基于Wasserstein距离的两阶段分布鲁棒优化模型是一种有效的处理不确定性和复杂性的优化方法。通过对偶转化和线性决策方法的应用,我们可以将复杂的原始问题转化为更易求解的形式,提高决策的鲁棒性和适应性。未来的研究可以进一步探索模型在不同领域的应用和扩展,以及与其他优化方法的结合和比较。
通过上述改进,两阶段DRO有望在更多领域实现经济性与鲁棒性的最优平衡,成为应对不确定性的核心工具。
📚2 运行结果
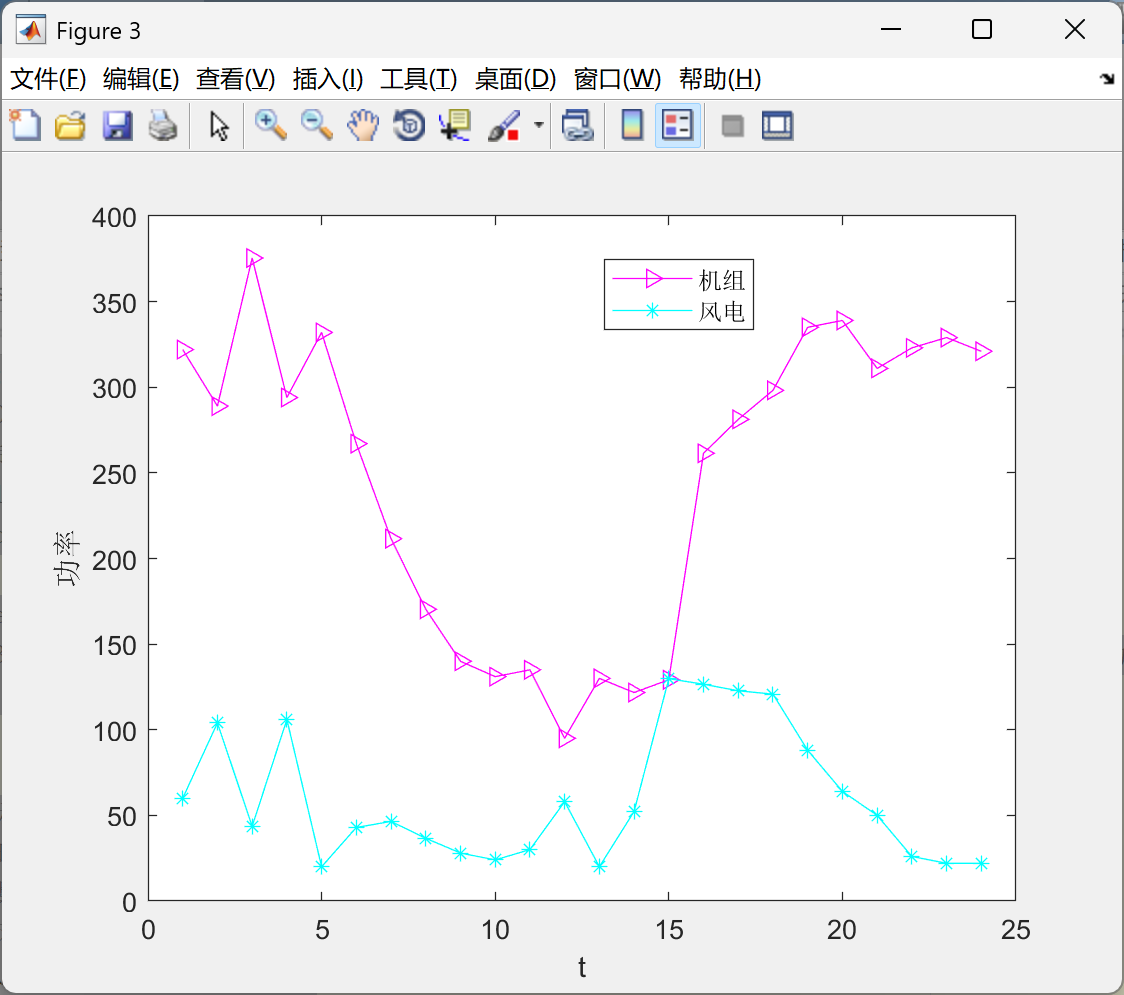
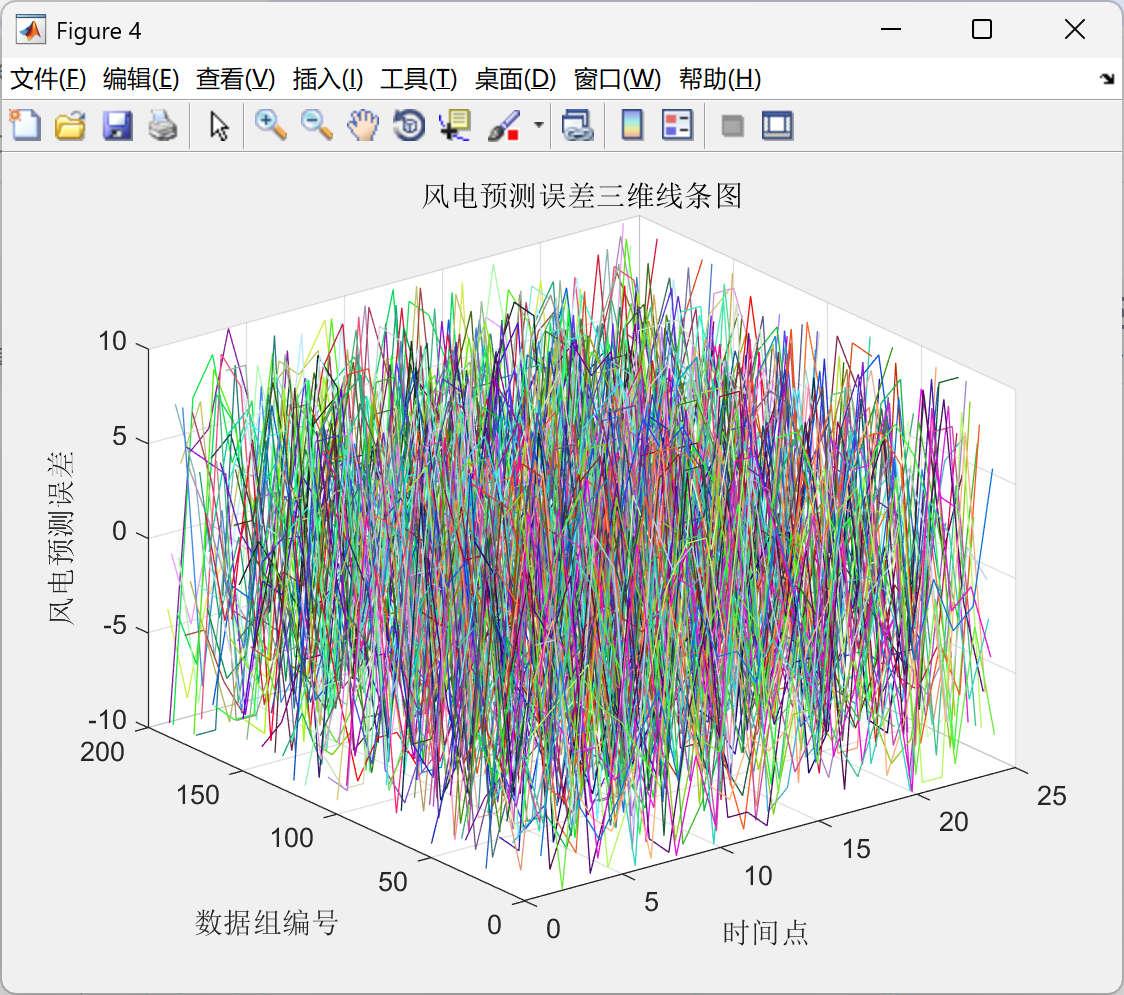
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
[1]许乃祥.基于改进的RNGA算法求解两阶段分布鲁棒优化群体共识模型[J].Advances in Applied Mathematics, 2022, 11.
[2]曹小鹿,辛云宏.基于Wasserstein距离概率分布模型的非线性降维[J].计算机应用, 2017, 37(10):4.
🌈4 Matlab代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取





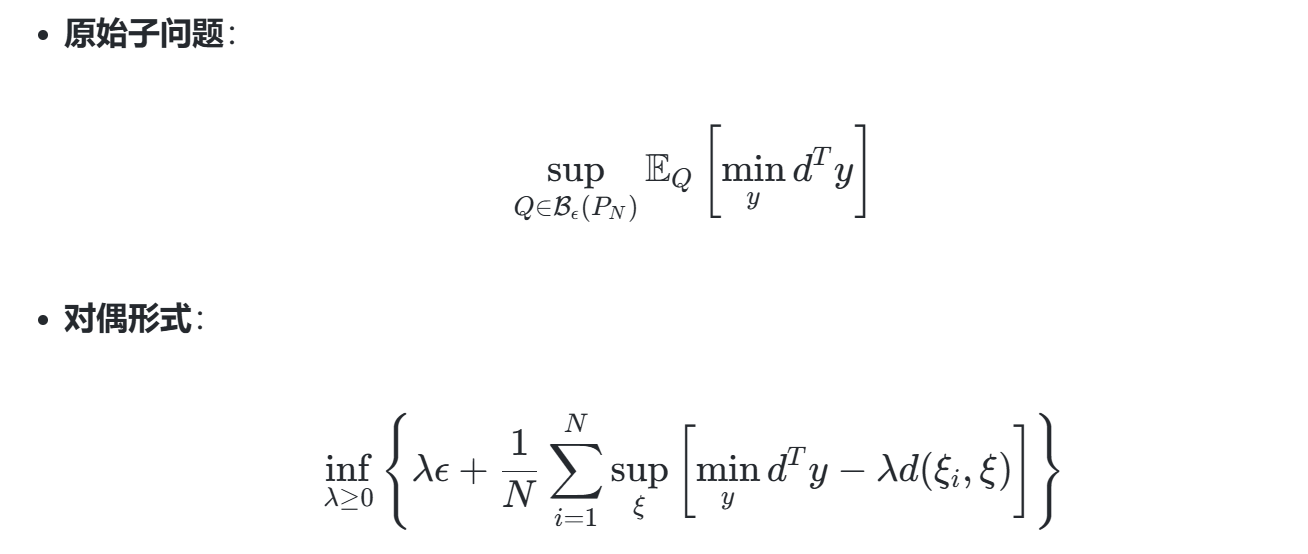
















 4179
4179

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








