💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
摘要:本文提出了一种数据驱动的结构健康监测(SHM)方法,用于进行原位评估结构健康状态,即损伤位置和程度,在其中利用了选定位置的引导式兰姆波响应。该方法由离线和在线两个阶段组成。离线阶段的目标是进行数据维度降低,并建立传感器数据与损伤状态之间的映射关系。首先,通过高保真有限元方法(ABAQUS软件)进行模拟,建立了全面的数据库,以确定在各种预先确定的结构损伤条件下的引导式兰姆波响应(例如,位移和加速度)。然后,应用适当正交分解(POD)方法从每个模拟情况下提取关键特征。最后,开发了基于神经网络的代理模型,以将损伤状态与POD的模态系数相关联。在线阶段的目标是利用有限的传感器测量量来量化损伤位置和程度。采用间隙适当正交分解(GPOD)来基于有限的传感器数据重建全场信息。随后,利用离线阶段开发的代理模型推导出相关的损伤程度和位置。提出的数据驱动型SHM方法利用从梁和板示例中获取的模拟数据进行了全面验证。评估值与实际损伤值之间的最大误差在10%以内。还进行了参数研究,以探究使用不同传感器布置和传感器类型进行损伤检测的效果。总之,提出的方法可能成为航空航天结构的高效损伤检测技术。
关键词:结构健康监测(SHM)引导式兰姆波 适当正交分解(POD)间隙POD 神经网络 损伤估计
不同的结构已经被广泛应用于航空航天、汽车、民用以及机械领域。航空航天结构展现出多种多样的结构类型,包括梁、板、壳体等。它们受到动态载荷的作用,这会导致内部缺陷在某一点生长并合并。这可能导致系统级的灾难性失败。此外,撞击事件也会对航空航天结构造成损伤。这些损伤模式随着撞击条件而变化。它们会改变结构的材料或几何属性,并影响系统的整体性能。通常,损伤以裂纹、孔洞、分层或连接处的不连续形式存在。在许多情况下,视觉检查无法在其初始阶段检测到小的损伤。因此,需要结构健康监测(SHM)技术来检测损伤、评估健康状态并预测航空航天结构的寿命周期。本次努力的新颖之处包括:(1)将POD、传感器布置优化、神经网络和GPOD技术应用于具有大数据量的时间相关信号中,整个时间域内的动态数据作为损伤检测和识别的整体特征。这与之前的工作形成鲜明对比,之前的工作绕过了逆向损伤问题(即,损伤定位和严重程度检测),而是利用静态测量数据,例如静态应变(Mainini和Willcox 2015)作为推断指标;以及(2)采用引导式兰姆波响应来进行有效的损伤检测,使用数据驱动建模方法,而不是传统的损伤三角定位方法。如前所述,传统的基于波的SHM方法广泛用于根据飞行时间(TOF)和波速计算进行实时工程应用中的损伤检测。因此,选择这些波响应来展示所提出的用于原位损伤检测的数据驱动方法。

本文开发了一种基于数据驱动的结构健康监测(SHM)新方法,利用导波(Lamb波)响应实现。该方法分为离线和在线两个阶段。在离线阶段,通过高保真有限元仿真生成梁和板结构中的导波响应(即位移和加速度),以构建全面的数据库。基于POD(Proper Orthogonal Decomposition,正交分解)的代理模型被开发出来,用于在低维度中表示大量的波传播数据。只需要少数几个主要的POD模态即可准确重构波传播响应。在梁结构中,共提取了101个POD模态,其中只有前18个模态被保留用于准确的数据重构。类似地,在板结构中,只有11个POD模态被用于数据重构。相应地,开发了神经网络代理模型,以关联这些POD模态系数与梁和板结构中的损伤位置和程度。
在在线阶段,利用稀疏传感器数据通过GPOD方法重构全场测量数据。最终,通过应用离线阶段开发的代理模型,并结合添加了10%噪声的仿真响应,我们能够推断损伤的位置和程度。推断值与实际值之间的最大误差在10%以内。总之,所提出的基于数据驱动的SHM方法展示了在航空航天结构中实现实时损伤检测的潜力。
一、技术原理:数据驱动的SHM系统与兰姆波损伤检测机制
1. SHM系统核心组成
数据驱动的SHM系统通过传感器网络实时采集结构响应信号(如振动、应变、位移),结合特征提取与模式识别评估结构健康状态。核心模块包括:
- 数据采集:加速度计、应变片、光纤传感器、压电换能器(PZT)等。
- 数据传输:有线/无线方式传输海量数据至监测中心。
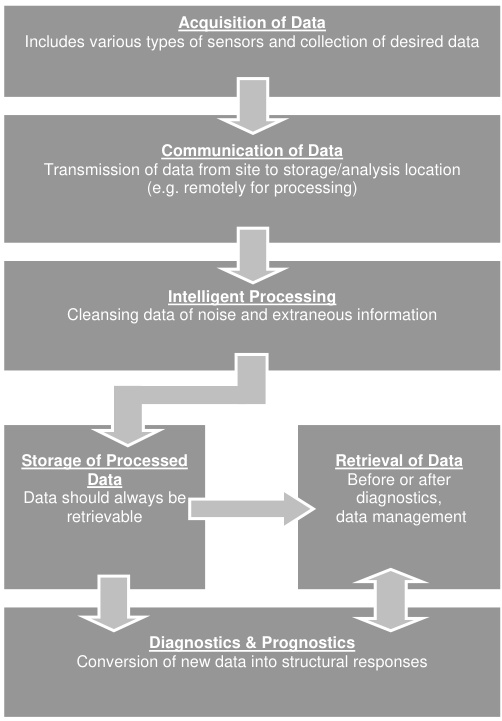
- 数据处理:包括数据清洗、特征提取、模式识别(如小波变换、压缩感知)及健康评估。
- 评估决策:基于诊断结果发布预警并提供维护策略。
2. 兰姆波在损伤检测中的独特优势
兰姆波(Lamb Wave)是板状结构中传播的弹性导波,适用于航空航天薄壁结构(如机翼、蒙皮),其优势包括:
- 长距离传播与低衰减:单次激励可覆盖大面积结构。
- 对微小损伤敏感:可检测裂纹、分层、腐蚀等缺陷。
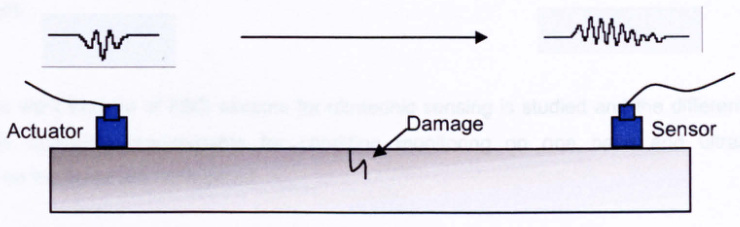
- 穿透性:可穿透涂层和绝缘层,检测内部损伤。
- 多模态特性:对称模式(S0)和反对称模式(A0)分别对厚度变化和表面损伤敏感。
3. 损伤检测机制
当兰姆波在结构中传播时,损伤区域会散射/反射波信号,导致以下变化:
- 传播时间延迟:损伤散射波到达传感器的时间晚于直接波。
- 幅值与相位变化:损伤导致能量衰减或波形畸变。
- 模式转换:损伤可能激发新的波模式(如S0→A0)。
通过分析这些变化,可定位损伤并量化程度。
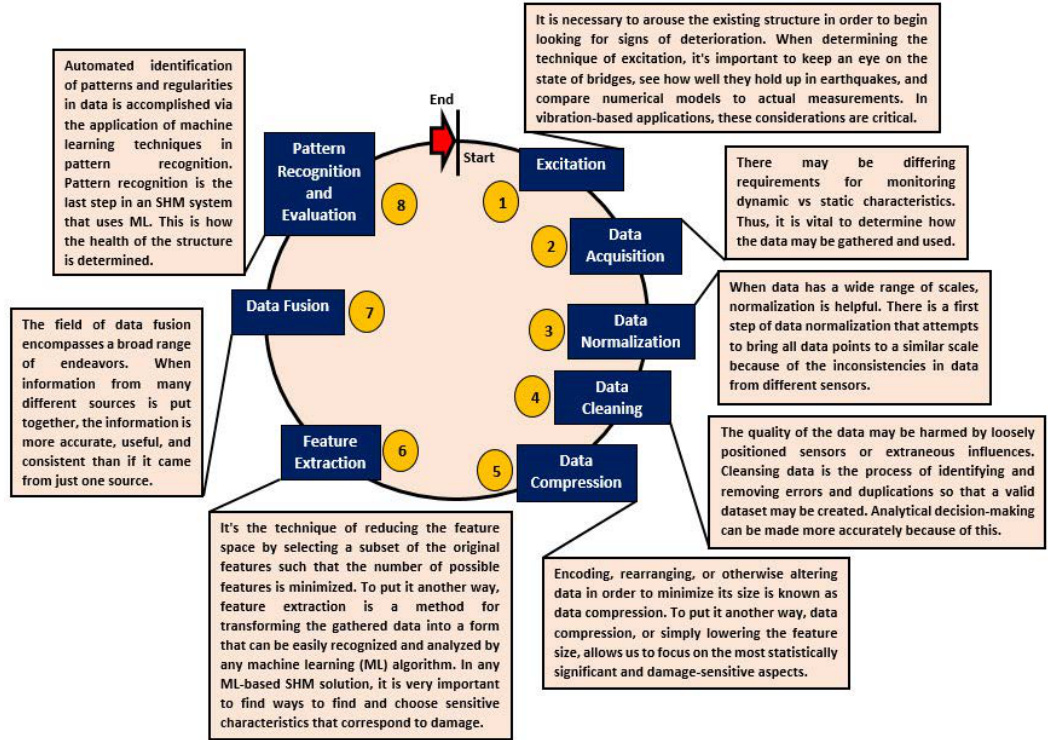
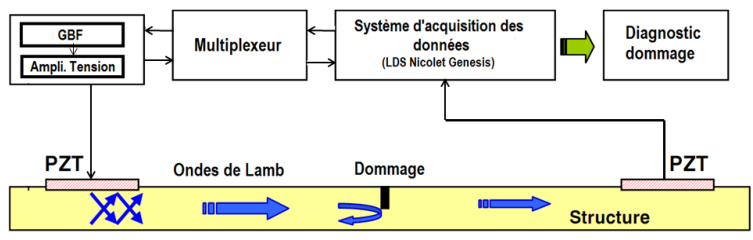
二、核心技术:引导式兰姆波响应的实现方法
1. 传感器布局优化
- 阵列设计:采用压电换能器(PZT)阵列,通过对称布置或稀疏阵列减少传感器数量。
- 热点区域聚焦:基于损伤容限分析预测易损位置,针对性部署传感器。
- 路径规划:设计波传播路径覆盖关键区域(如铆钉孔、焊缝)。
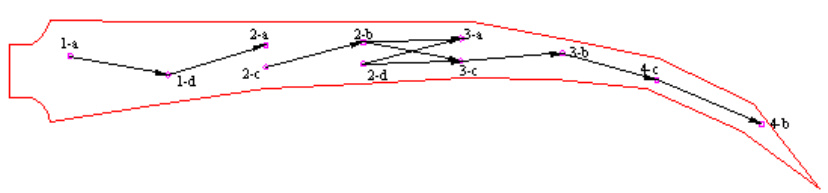
2. 信号激励与单模控制
为减少多模态叠加导致的信号复杂性:
- 频率调谐:选择特定频率激发单一模式(如S0模式)。
- 激励器配置:优化PZT尺寸和形状(如矩形薄片)抑制A0模式。
- 信号调制:使用窄带脉冲或编码激励增强信噪比。
3. 信号处理与特征提取
| 技术 | 功能 | 应用案例 |
|---|---|---|
| 时频分析 | 分离多模态信号,提取群速度/相速度 | 小波变换、维格纳-维尔分布 |
| 数据压缩 | 降低存储与传输开销 | 压缩感知 |
| 模式分离算法 | 分解叠加信号为单一模式 | Vold-Kalman滤波器 |
| 无基准损伤检测 | 避免依赖初始健康数据,通过对称响应分析定位损伤 | 皮尔逊相关系数法 |
| 概率成像技术 | 基于散射波到达时间生成损伤概率分布图 | 椭圆轨迹法 |
4. 数据驱动的损伤量化模型
- 离线建模阶段:
- 通过 有限元模拟(如ABAQUS) 构建不同损伤场景的兰姆波响应数据库。
- 使用 适当正交分解(POD) 提取关键特征模态。
- 训练神经网络代理模型,关联损伤参数(位置、程度)与POD模态系数。
- 在线监测阶段:
- 利用 间隙POD(GPOD) 根据有限传感器数据重建全场响应。
- 调用代理模型实时输出损伤位置与程度,误差可控制在10%以内。
三、航空航天应用的特殊挑战与解决方案
1. 核心挑战
- 材料复杂性:复合材料各向异性导致损伤模式多样(如分层、微裂纹)。
- 结构尺度大:飞机外壳等大型部件需高效全覆盖检测。
- 环境干扰:极端温度、振动噪声影响信号稳定性。
- 实时性要求:飞行中需快速识别损伤以调整任务规划。
2. 针对性解决方案
| 挑战 | 技术对策 | 依据 |
|---|---|---|
| 复合材料检测 | 结合深度学习的轻量化模型(如组卷积网络),提升对分层/裂纹的识别精度 | 实验准确率可达100% |
| 大尺度覆盖 | 稀疏传感器阵列 + 兰姆波长距离传播特性 | 减少50%传感器数量 |
| 环境鲁棒性 | 无基准对称响应分析 + 时频域噪声滤波 | 避免温度漂移影响 |
| 实时诊断 | 边缘计算部署轻量化模型 + 在线GPOD重建 | 8轮训练即达高精度 |
3. 前沿技术融合
- 数字孪生:结合物理模型与实时数据动态预测损伤演化。
- 多传感器融合:集成光纤传感器与PZT阵列,提升监测维度。
- 人工智能:
- 轻量化CNN处理原始波形数据,直接输出损伤图像。
- 强化学习优化传感器布局与诊断策略。
四、总结与展望
基于引导式兰姆波的数据驱动SHM技术,通过优化传感器布局、单模激励控制、先进信号处理及AI模型,实现了航空航天结构损伤的原位高精度检测(误差≤10%)。未来发展方向包括:
- 多功能集成:将SHM系统嵌入结构本体,形成“自感知”智能结构。
- 跨尺度监测:从微裂纹到宏观损伤的多尺度关联模型。
- 标准化挑战:制定统一的兰姆波检测协议与损伤量化标准。
此技术不仅显著提升飞行安全性与维护效率,还可推广至风电叶片、桥梁等大型基础设施的健康监测。
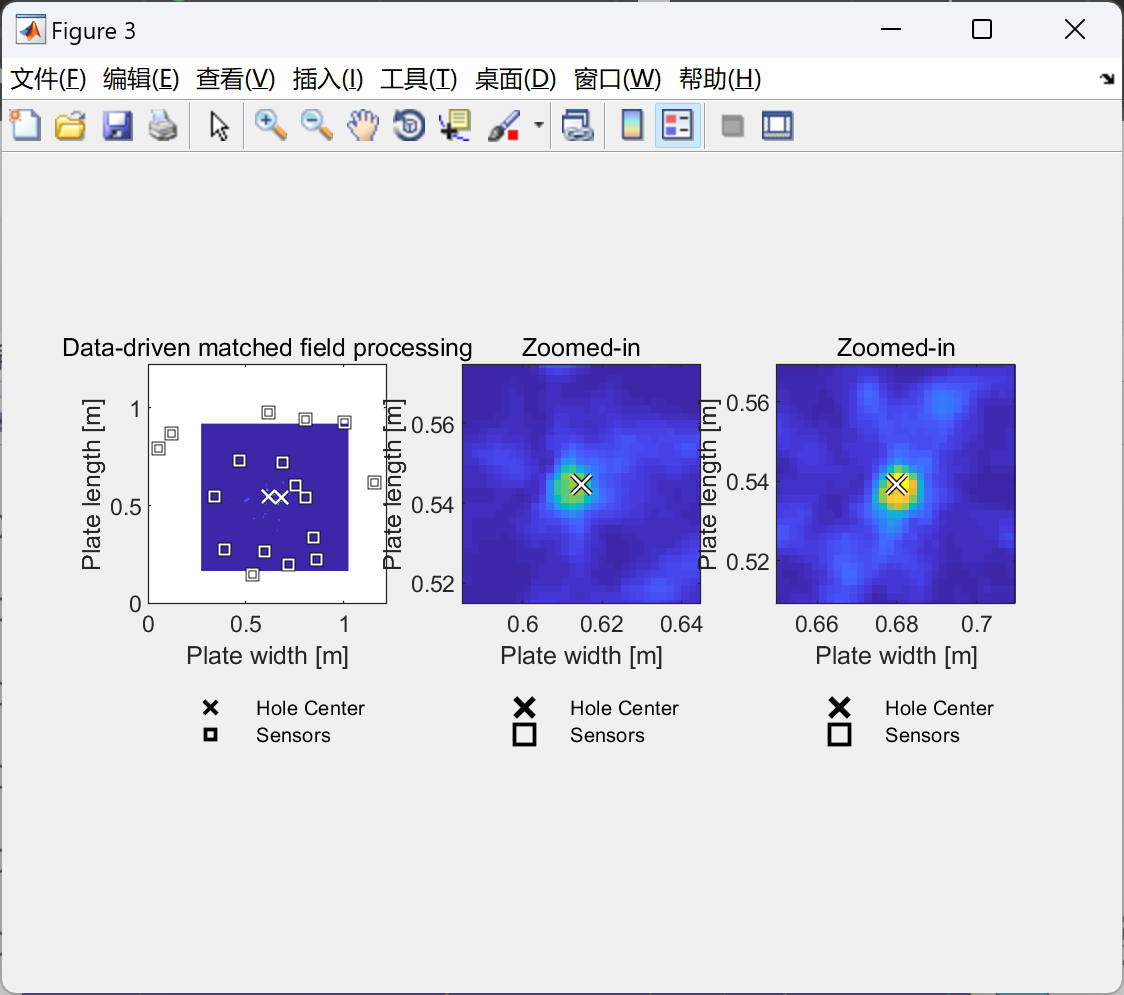
📚2 运行结果
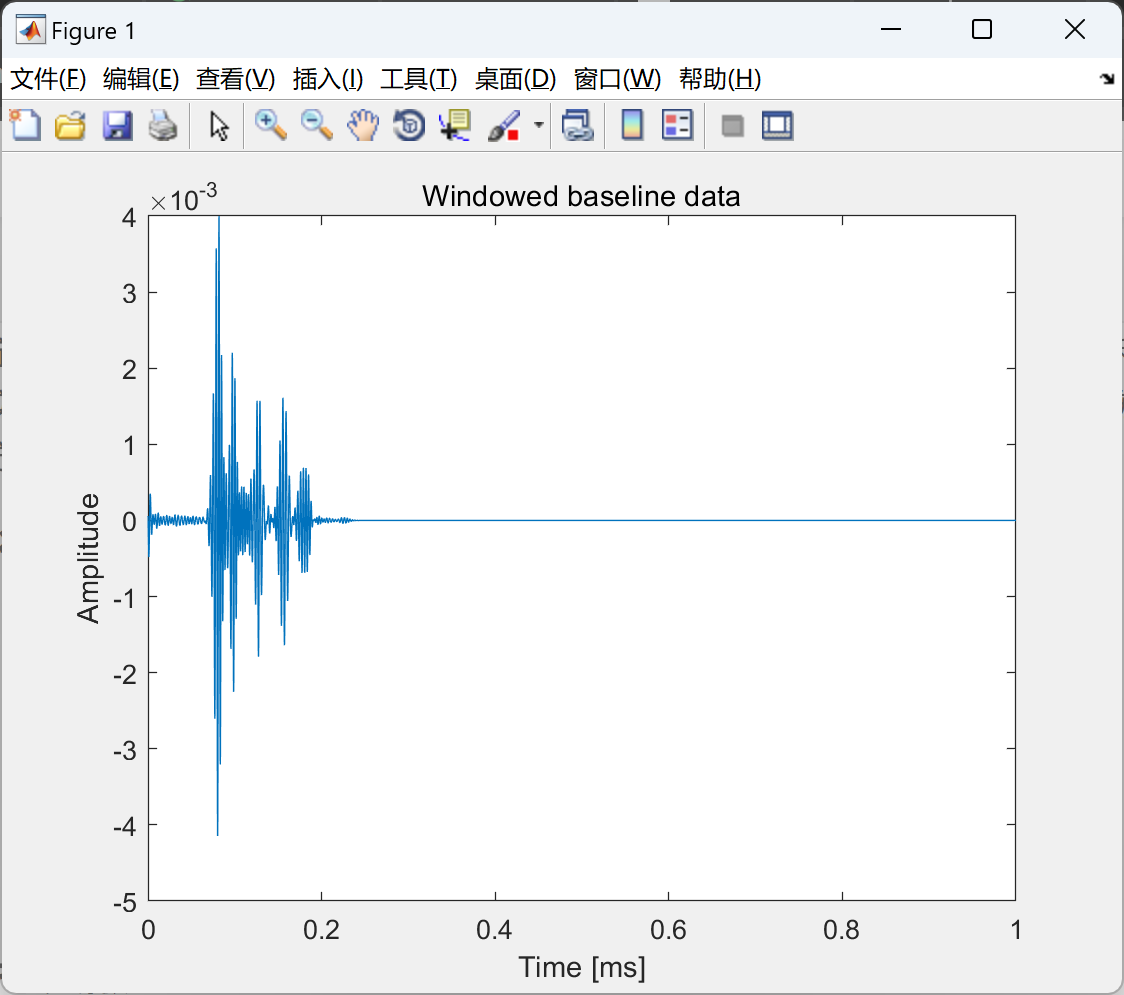

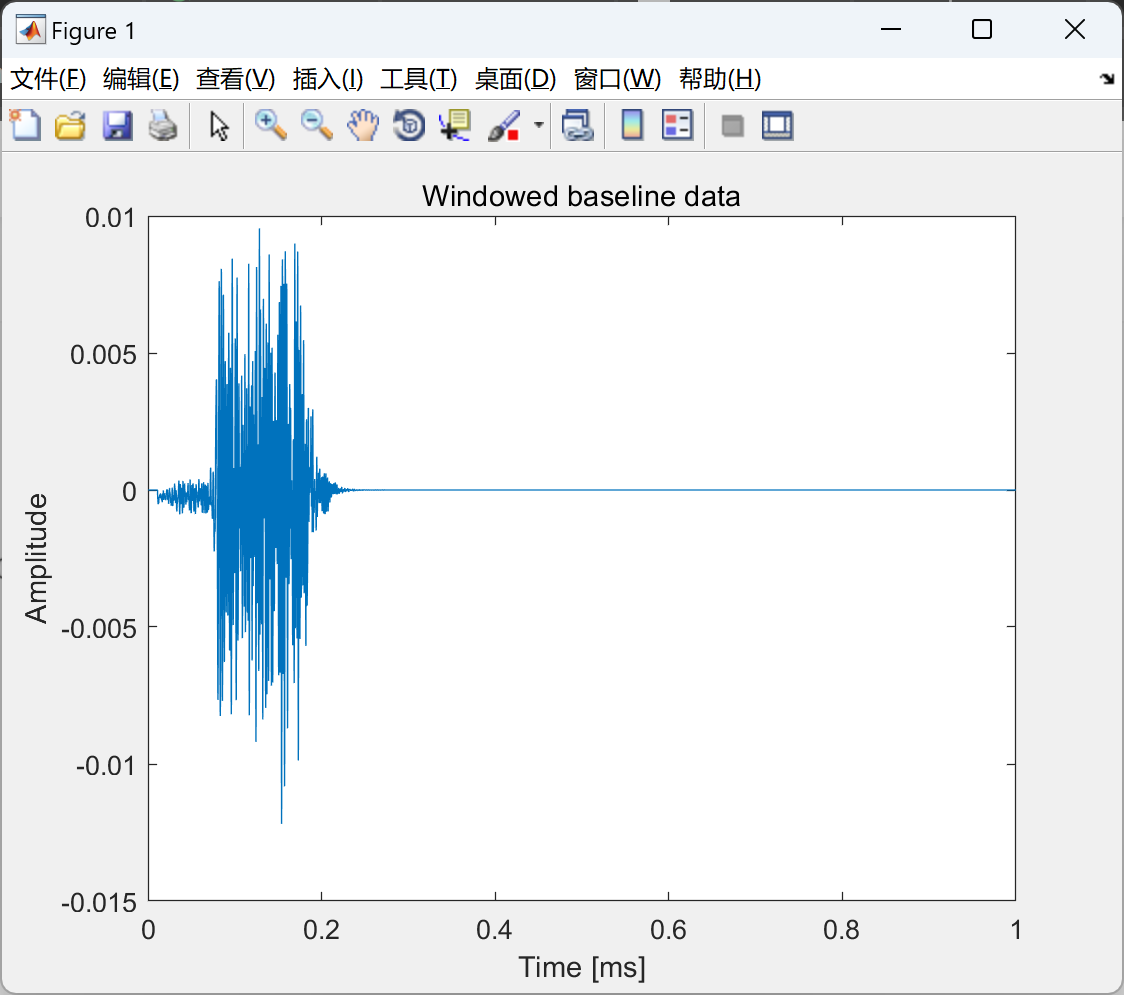
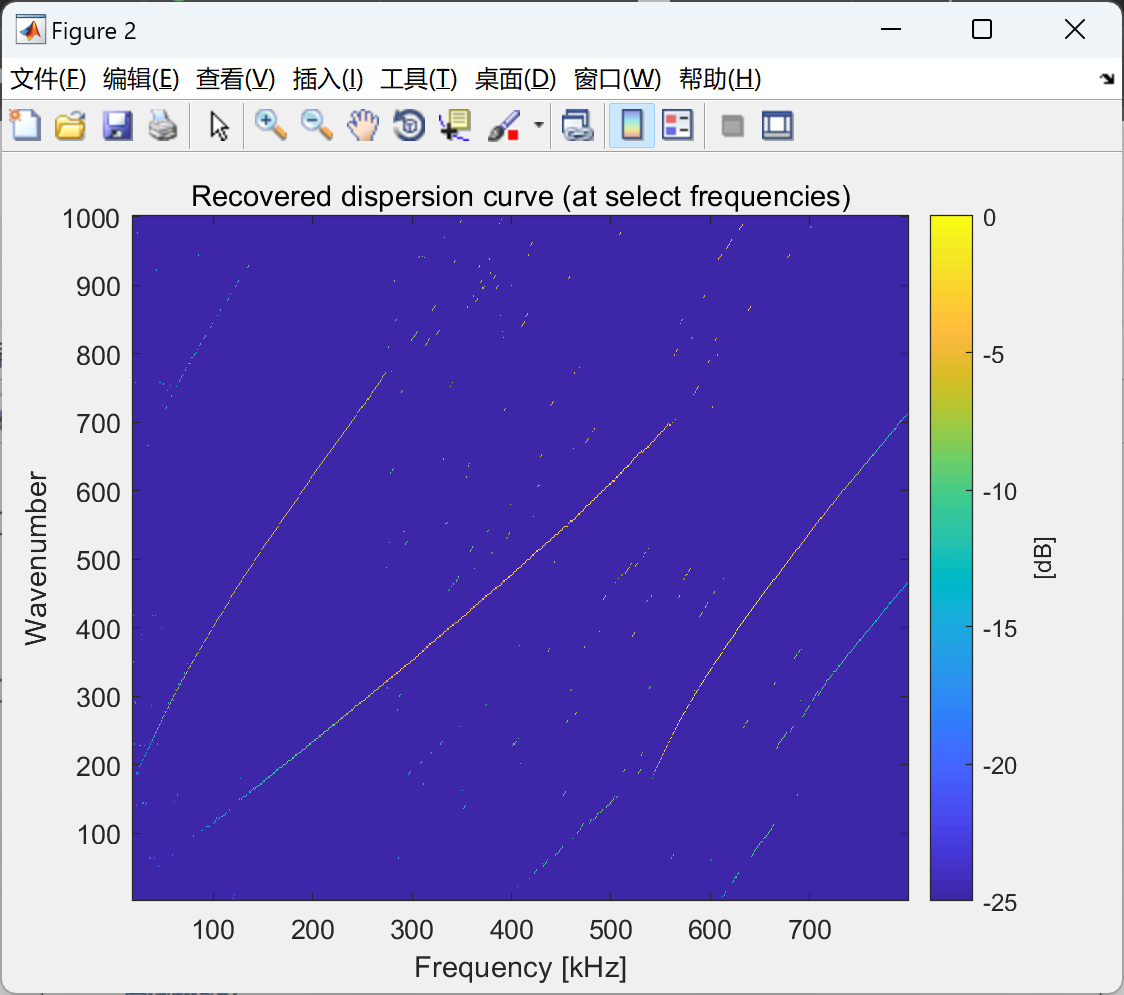
部分代码:
% EXPERIMENT INFORMATION
fl = 3; % 1: one 0.5cm hole
% 2: one 0.75cm hole
% 3: two 0.75cm holes
% SWA INFORMATION
fn = 20:1:800; % Frequencies
k = (2:2:1000).'; % Wavenumbers for dispersion curves
sns = 1:1:17; % Sensors to use (1:17 is the largest range)
% LOCALIZATION INFORMATION
W = 0.75; % Window size around defect
Nx = 400; % Number of pixels in x direction
Ny = 400; % Number of pixels in y direction
% WINDOWING INFORMATION
vwin = 2000; % Velcoity (in m/s) for velocity window
c = 5110.83; % Velocity for delay and sum
%%
% ---------------------------------------------
% GET DATA
% ---------------------------------------------
% DETERMINE THE DATA
basename = 'data_20121029_localize_baseline';
if fl == 1, dataname = 'data_20121029_localize_hole_05cmC';
elseif fl == 2, dataname = 'data_20121029_localize_hole_075cmC';
elseif fl == 3, dataname = 'data_20121029_localize_2holes_075cmC';
end
% GET DATA (BUILD A MAT FILE IF NOT AVAILABLE)
if exist([basename '.mat'],'file')
load([basename '.mat']);
else
[metab, cfgb] = extract_data(str2func(basename), 1:34);
save([basename '.mat'], 'metab', 'cfgb');
end
if exist([dataname '.mat'],'file')
load([dataname '.mat']);
else
[metas, cfgs] = extract_data(str2func(dataname), 1:34);
save([dataname '.mat'], 'metas', 'cfgs');
end
metab = filter_tn(filter_rn(metab, sns), sns);
metas = filter_tn(filter_rn(metas, sns), sns);
%%
% ---------------------------------------------
% GET DISPERSION CURVES
% ---------------------------------------------
% COMPUTE DISTANCES BETWEEN SENSORS
Sx = metas.Sx; % Hole location
Tx = arrayfun(@(ii) (metab.Tx{ii}.'*ones(1,size(metab.Rx{ii},1))).', 1:numel(metab.Rx), 'UniformOutput', false); % Transmitter locations
d = diag(dist(cell2mat(metab.Rx), cell2mat(Tx.').')); % Distance between each reciever and transmitter
% PRE-PROCESS SIGNALS
xb = cell2mat(metab.x.'); % Baseline signal
xb = xb - mean(xb,2); % Remove means
xb(1:110,:) = 0; % Remove cross-talk
xb = velwindow(xb, d, vwin/metab.Fs); % Velocity-based window
Xb = fft(xb); % Fourier transform
xs = cell2mat(metas.x.'); % Signal with target
xs = xs - mean(xs,2); % Remove means
xs(1:110,:) = 0; % Remove cross-talk
xs = velwindow(xs, d, vwin/metab.Fs); % Velocity-based window
Xs = fft(xs); % Fourier transform
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。





















 685
685

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








